全一卷
1.已知集合 则
则
 则
则
| A.[2,3] | B.( -2,3 ] | C.[1,2) | D. |
2.已知互相垂直的平面 交于直线l.若直线m,n满足m∥α,n⊥β,则
交于直线l.若直线m,n满足m∥α,n⊥β,则
 交于直线l.若直线m,n满足m∥α,n⊥β,则
交于直线l.若直线m,n满足m∥α,n⊥β,则| A.m∥l | B.m∥n | C.n⊥l | D.m⊥n |
3.在平面上,过点P作直线l的垂线所得的垂足称为点P在直线l上的投影.由区域
 中的点在直线x+y
中的点在直线x+y 2=0上的投影构成的线段记为AB,则│AB│=
2=0上的投影构成的线段记为AB,则│AB│=
 中的点在直线x+y
中的点在直线x+y 2=0上的投影构成的线段记为AB,则│AB│=
2=0上的投影构成的线段记为AB,则│AB│=A.2 | B.4 | C.3 | D.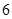 |
4.命题“ ,使得
,使得 ”的否定形式是( )
”的否定形式是( )
 ,使得
,使得 ”的否定形式是( )
”的否定形式是( )A. ,使得 ,使得 | B. ,使得 ,使得 |
C. ,使得 ,使得 | D. ,使得 ,使得 |
5.设函数 ,则
,则 的最小正周期
的最小正周期
 ,则
,则 的最小正周期
的最小正周期| A.与b有关,且与c有关 |
| B.与b有关,但与c无关 |
| C.与b无关,且与c无关 |
| D.与b无关,但与c有关 |
6.如图,点列{An},{Bn}分别在某锐角的两边上,且 ,
, .(
.( )
)
若

 ,
, .(
.( )
)若


A. 是等差数列 是等差数列 |
B. 是等差数列 是等差数列 |
C. 是等差数列 是等差数列 |
D. 是等差数列 是等差数列 |
7.已知椭圆C1: +y2=1(m>1)与双曲线C2:
+y2=1(m>1)与双曲线C2: –y2=1(n>0)的焦点重合,e1,e2分别为C1,C2的离心率,则
–y2=1(n>0)的焦点重合,e1,e2分别为C1,C2的离心率,则
 +y2=1(m>1)与双曲线C2:
+y2=1(m>1)与双曲线C2: –y2=1(n>0)的焦点重合,e1,e2分别为C1,C2的离心率,则
–y2=1(n>0)的焦点重合,e1,e2分别为C1,C2的离心率,则| A.m>n且e1e2>1 | B.m>n且e1e2<1 | C.m<n且e1e2>1 | D.m<n且e1e2<1 |
8.已知实数a,b,c.
| A.若|a2+b+c|+|a+b2+c|≤1,则a2+b2+c2<100 |
| B.若|a2+b+c|+|a2+b–c|≤1,则a2+b2+c2<100 |
| C.若|a+b+c2|+|a+b–c2|≤1,则a2+b2+c2<100 |
| D.若|a2+b+c|+|a+b2–c|≤1,则a2+b2+c2<100 |
9.若抛物线y2=4x上的点M到焦点的距离为10,则M到y轴的距离是_______.
10.某几何体的三视图如图所示(单位:cm),则该几何体的表面积是______cm2,体积是______cm3.


11.已知a>b>1.若logab+logba= ,ab=ba,则a= ,b= .
,ab=ba,则a= ,b= .
 ,ab=ba,则a= ,b= .
,ab=ba,则a= ,b= .12. 设数列{an}的前n项和为Sn.若S2=4,an+1=2Sn+1,n∈N*,则a1=________,S5=________.
13.如图,在 ABC中,AB=BC=2,∠ABC=120°.若平面ABC外的点P和线段AC上的点D,满足PD=DA,PB=BA,则四面体PBCD的体积的最大值是 .
ABC中,AB=BC=2,∠ABC=120°.若平面ABC外的点P和线段AC上的点D,满足PD=DA,PB=BA,则四面体PBCD的体积的最大值是 .
 ABC中,AB=BC=2,∠ABC=120°.若平面ABC外的点P和线段AC上的点D,满足PD=DA,PB=BA,则四面体PBCD的体积的最大值是 .
ABC中,AB=BC=2,∠ABC=120°.若平面ABC外的点P和线段AC上的点D,满足PD=DA,PB=BA,则四面体PBCD的体积的最大值是 .
14.已知向量a,b,|a| =1,|b|=2,若对任意单位向量e,均有|a·e|+|b·e|
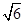 ,则a·b的最大值是 .
,则a·b的最大值是 .

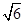 ,则a·b的最大值是 .
,则a·b的最大值是 .15.已知 ,则
,则
_________ , =
=__________ .
 ,则
,则
 =
=16.在 中,内角
中,内角 所对的边分别为
所对的边分别为 ,已知
,已知 .
.
(1)证明: ;
;
(2)若 的面积
的面积 ,求角
,求角 的大小.
的大小.
 中,内角
中,内角 所对的边分别为
所对的边分别为 ,已知
,已知 .
.(1)证明:
 ;
;(2)若
 的面积
的面积 ,求角
,求角 的大小.
的大小.17.如图,在三棱台 中,平面
中,平面 平面
平面 ,
, ,BE=EF=FC=1,BC=2,AC=3.
,BE=EF=FC=1,BC=2,AC=3.

(Ⅰ)求证:EF⊥平面ACFD;
(Ⅱ)求二面角B-AD-F的平面角的余弦值.
 中,平面
中,平面 平面
平面 ,
, ,BE=EF=FC=1,BC=2,AC=3.
,BE=EF=FC=1,BC=2,AC=3.
(Ⅰ)求证:EF⊥平面ACFD;
(Ⅱ)求二面角B-AD-F的平面角的余弦值.
18.已知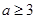 ,函数F(x)=min{2|x−1|,x2−2ax+4a−2},
,函数F(x)=min{2|x−1|,x2−2ax+4a−2},
其中min{p,q}=
(Ⅰ)求使得等式F(x)=x2−2ax+4a−2成立的x的取值范围;
(Ⅱ)(ⅰ)求F(x)的最小值m(a);
(ⅱ)求F(x)在区间[0,6]上的最大值M(a).
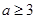 ,函数F(x)=min{2|x−1|,x2−2ax+4a−2},
,函数F(x)=min{2|x−1|,x2−2ax+4a−2},其中min{p,q}=

(Ⅰ)求使得等式F(x)=x2−2ax+4a−2成立的x的取值范围;
(Ⅱ)(ⅰ)求F(x)的最小值m(a);
(ⅱ)求F(x)在区间[0,6]上的最大值M(a).
19.如图,设椭圆 (a>1).
(a>1).

(Ⅰ)求直线y=kx+1被椭圆截得的线段长(用a、k表示);
(Ⅱ)若任意以点A(0,1)为圆心的圆与椭圆至多有3个公共点,求椭圆离心率的取值范围.
 (a>1).
(a>1).
(Ⅰ)求直线y=kx+1被椭圆截得的线段长(用a、k表示);
(Ⅱ)若任意以点A(0,1)为圆心的圆与椭圆至多有3个公共点,求椭圆离心率的取值范围.
20.设数列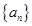 满足
满足 ,
, .
.
(Ⅰ)证明: ,
, ;
;
(Ⅱ)若 ,
, ,证明:
,证明: ,
, .
.
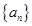 满足
满足 ,
, .
.(Ⅰ)证明:
 ,
, ;
;(Ⅱ)若
 ,
, ,证明:
,证明: ,
, .
. 搜索
搜索
 难度系数:0.65
难度系数:0.65  答案解析
答案解析
 有奖纠错
有奖纠错
