搜索
全一卷
难度系数：0.65 
答案解析
有奖纠错
1．三角形的三条边长均为正整数，其中有一条边长为4，但它不是最短的边，这样不同的三角形共有
| A．6个 | B．7个 | C．8个 | D．9个 |
2．若
，则必有
，则必有A． |
B． |
C． |
D． |
3．在轴截面顶角为直角的圆锥内，作一内接圆柱，若这圆柱的全面积等于这圆锥的侧面积，则这圆锥顶点至圆柱上底面的距离等于圆锥母线长的
A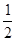． | B． | C． | D． . |
4．点P（0，2）关于直线
的对称点坐标是
的对称点坐标是| A．（-2，0） | B．（-1，0） | C．（0.-1） | D． . |
5．
除以13的余数是
除以13的余数是| A．1 | B．2 | C．3 | D．7 |
6．已知函数
对任意实数x都有意义，又直线
的倾角为θ，则θ的值等于
对任意实数x都有意义，又直线
的倾角为θ，则θ的值等于A． |
B． |
C． |
D． |
7．已知三个实数
其中0.9<a<1，这三个数的大小关系是
其中0.9<a<1，这三个数的大小关系是A． | B． | C． | D． |
8．设a为正数，而
，
，是
平面内的点集，则
的一个充分必要条件是
，
，是
平面内的点集，则
的一个充分必要条件是| A．a=2 | B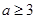． | C． | D． |
9．若极坐标方程
是一圆锥曲线，则它的焦点到其相应准线的距离是
是一圆锥曲线，则它的焦点到其相应准线的距离是| A． | B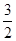． | C．1 | D．2 |
10．今有一角币1张，二角币1张，五角币1张，一元币4张，五元币2张，用这些纸币任意付款，则可以付出不同数额的款子共有
| A．30种 | B．29种 | C．120种 | D．119种. |
11．若曲线
和三直线x=1，y=1及y=x+1相切，则
和三直线x=1，y=1及y=x+1相切，则| A．a=b=c | B．a=b=-c | C．a=-b=c | D．-a=b=c. |
12．已知
，当Z是复平面上第三象限内的点时，实数x的取值范围是
，当Z是复平面上第三象限内的点时，实数x的取值范围是A． | B． | C． | D． . |
13．一个等比数列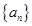
的首项
，它的前11项的几何平均数为
，若前11项中抽去一项后的几何平均数为
，则抽去的项是
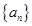的首项
，它的前11项的几何平均数为
，若前11项中抽去一项后的几何平均数为
，则抽去的项是| A．第8项 | B．第9项 | C．第10项 | D．第11项 |
14．
和
两者大小关系是（其中e是自然对数的底，π是圆周率）
和
两者大小关系是（其中e是自然对数的底，π是圆周率）A． |
B． |
| C． |
| D．不能确定它们大小关系。 |
15．A，B，C，D是空间不共面的四点，它们到平面a的距离之比依次为1：1：1：2，则满足条件的平面a的个数是：
| A．1 | B．4 | C．7 | D．8. |
16．已知A，B，M，N为非空集，
，M={A的真子集}，N={B的真子集}，那么
______.
，M={A的真子集}，N={B的真子集}，那么
______.17．已知函数
.那么它的值域是____
.那么它的值域是____18．抛物线
（a为非零常数）的顶点在曲线_____上.
（a为非零常数）的顶点在曲线_____上.19．6人划船，左右各3人，其中2人只能划左桨，1人只能划右桨，这样他们的不同坐法共有_____种.
20．已知方程
表示两条直线，则实数
______
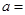表示两条直线，则实数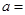
______21．空间四边形的两组对边的平方和相等，那么它的两条对角线所成的角是______度.
22．用正方形完全盖住边长分别为3cm、4cm、5cm的一个三角形，那么这个正方形的最小边长是______
23．已知：
， 
，
，
，那么
的值是______.
， 
，
，
，那么
的值是______.24．制作一个底圆直径为4cm圆柱形的容器，要内装直径为2cm的钢珠26只，那么这容器的高至少是_____cm（精确到0.1cm）.
