全一卷
1.在实数 中,最小的数是( )
中,最小的数是( )
 中,最小的数是( )
中,最小的数是( )A. | B. | C. | D.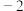 |
2.在如图所示的几何体中,俯视图和左视图相同的是( )
A. | B. | C. | D. |
3.为庆祝神舟十四号发射成功,学校开展航天知识竞赛活动.经过几轮筛选,本班决定从甲、乙、丙、丁四名同学中选择一名同学代表班级参加比赛,经过统计,四名同学成绩的平均数(单位:分)及方差(单位:分2)如表所示:
如果要选一名成绩好且状态稳定的同学参赛,那么应该选择( )
甲 | 乙 | 丙 | 丁 | |
平均数 |
|
|
|
|
方差 |
|
|
|
|
| A.甲 | B.乙 | C.丙 | D.丁 |
4.已知反比例函数 的图像经过点
的图像经过点 ,那么该反比例函数图像也一定经过点( )
,那么该反比例函数图像也一定经过点( )
 的图像经过点
的图像经过点 ,那么该反比例函数图像也一定经过点( )
,那么该反比例函数图像也一定经过点( )A. | B. | C. | D. |
5.不等式组 的解集,在数轴上表示正确的是( )
的解集,在数轴上表示正确的是( )
 的解集,在数轴上表示正确的是( )
的解集,在数轴上表示正确的是( )A. | B. |
C. | D. |
6.如图, ,
, ,
, 是
是 上的三点,若
上的三点,若 ,则
,则 的度数是( )
的度数是( )

 ,
, ,
, 是
是 上的三点,若
上的三点,若 ,则
,则 的度数是( )
的度数是( )
A. | B. | C. | D. |
7.如图,是由 个全等的等边三角形组成的图案,假设可以随机在图中取点,那么这个点取在阴影部分的概率是( )
个全等的等边三角形组成的图案,假设可以随机在图中取点,那么这个点取在阴影部分的概率是( )

 个全等的等边三角形组成的图案,假设可以随机在图中取点,那么这个点取在阴影部分的概率是( )
个全等的等边三角形组成的图案,假设可以随机在图中取点,那么这个点取在阴影部分的概率是( )
A. | B. | C. | D. |
8.我市某区为 万人接种新冠疫苗,由于市民积极配合这项工作,实际每天接种人数是原计划的
万人接种新冠疫苗,由于市民积极配合这项工作,实际每天接种人数是原计划的 倍,结果提前
倍,结果提前 天完成了这项工作.设原计划每天接种
天完成了这项工作.设原计划每天接种 万人,根据题意,所列方程正确的是( )
万人,根据题意,所列方程正确的是( )
 万人接种新冠疫苗,由于市民积极配合这项工作,实际每天接种人数是原计划的
万人接种新冠疫苗,由于市民积极配合这项工作,实际每天接种人数是原计划的 倍,结果提前
倍,结果提前 天完成了这项工作.设原计划每天接种
天完成了这项工作.设原计划每天接种 万人,根据题意,所列方程正确的是( )
万人,根据题意,所列方程正确的是( )A. | B. |
C. | D. |
9.下列关于二次函数 的图像和性质的叙述中,正确的是( )
的图像和性质的叙述中,正确的是( )
 的图像和性质的叙述中,正确的是( )
的图像和性质的叙述中,正确的是( )A.点 在函数图像上 在函数图像上 | B.开口方向向上 |
C.对称轴是直线 | D.与直线 有两个交点 有两个交点 |
10.如图,平面直角坐标系中,在直线 和
和 轴之间由小到大依次画出若干个等腰直角三角形(图中所示的阴影部分),其中一条直角边在
轴之间由小到大依次画出若干个等腰直角三角形(图中所示的阴影部分),其中一条直角边在 轴上,另一条直角边与
轴上,另一条直角边与 轴垂直,则第
轴垂直,则第 个等腰直角三角形的面积是( )
个等腰直角三角形的面积是( )

 和
和 轴之间由小到大依次画出若干个等腰直角三角形(图中所示的阴影部分),其中一条直角边在
轴之间由小到大依次画出若干个等腰直角三角形(图中所示的阴影部分),其中一条直角边在 轴上,另一条直角边与
轴上,另一条直角边与 轴垂直,则第
轴垂直,则第 个等腰直角三角形的面积是( )
个等腰直角三角形的面积是( )
A. | B. | C. | D. |
11.计算:
______ .

12.一副三角板如图摆放,直线 ,则
,则 的度数是
的度数是______ .

 ,则
,则 的度数是
的度数是
13.如图,在矩形 中,
中, 是
是 边上一点,且
边上一点,且 ,
, 与
与 相交于点
相交于点 ,若
,若 的面积是
的面积是 ,则
,则 的面积是
的面积是______ .

 中,
中, 是
是 边上一点,且
边上一点,且 ,
, 与
与 相交于点
相交于点 ,若
,若 的面积是
的面积是 ,则
,则 的面积是
的面积是
14.在创建“文明校园”的活动中,班级决定从四名同学(两名男生,两名女生)中随机抽取两名同学担任本周的值周长,那么抽取的两名同学恰好是一名男生和一名女生的概率是______ .
15.如图,在 中,
中, ,
, ,将
,将 绕点
绕点 逆时针旋转
逆时针旋转 ,得到
,得到 ,则点
,则点 到
到 的距离是
的距离是______ .

 中,
中, ,
, ,将
,将 绕点
绕点 逆时针旋转
逆时针旋转 ,得到
,得到 ,则点
,则点 到
到 的距离是
的距离是
16.快递员经常驾车往返于公司和客户之间.在快递员完成某次投递业务时,他与客户的距离 与行驶时间
与行驶时间 之间的函数关系如图所示(因其他业务,曾在途中有一次折返,且快递员始终匀速行驶),那么快递员的行驶速度是
之间的函数关系如图所示(因其他业务,曾在途中有一次折返,且快递员始终匀速行驶),那么快递员的行驶速度是______  .
.

 与行驶时间
与行驶时间 之间的函数关系如图所示(因其他业务,曾在途中有一次折返,且快递员始终匀速行驶),那么快递员的行驶速度是
之间的函数关系如图所示(因其他业务,曾在途中有一次折返,且快递员始终匀速行驶),那么快递员的行驶速度是 .
.
17.先化简,再求值: ,其中
,其中 .
.
 ,其中
,其中 .
.18.当我们将一条倾斜的直线进行上下平移时,直线的左右位置也发生着变化.下面是关于“一次函数图像平移的性质”的探究过程,请补充完整.

(1)如图 ,将一次函数
,将一次函数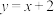 的图像向下平移
的图像向下平移 个单位长度,相当于将它向右平移了______个单位长度;
个单位长度,相当于将它向右平移了______个单位长度;
(2)将一次函数 的图像向下平移
的图像向下平移 个单位长度,相当于将它向______(填“左”或“右”)平移了______个单位长度;
个单位长度,相当于将它向______(填“左”或“右”)平移了______个单位长度;
(3)综上,对于一次函数 的图像而言,将它向下平移
的图像而言,将它向下平移 个单位长度,相当于将它向______(填“左”或“右”)(
个单位长度,相当于将它向______(填“左”或“右”)( 时)或将它向______(填“左”或“右”)(
时)或将它向______(填“左”或“右”)( 时)平移了
时)平移了 个单位长度,且
个单位长度,且 ,
, ,
,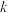 满足等式_______.
满足等式_______.

(1)如图
 ,将一次函数
,将一次函数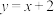 的图像向下平移
的图像向下平移 个单位长度,相当于将它向右平移了______个单位长度;
个单位长度,相当于将它向右平移了______个单位长度;(2)将一次函数
 的图像向下平移
的图像向下平移 个单位长度,相当于将它向______(填“左”或“右”)平移了______个单位长度;
个单位长度,相当于将它向______(填“左”或“右”)平移了______个单位长度;(3)综上,对于一次函数
 的图像而言,将它向下平移
的图像而言,将它向下平移 个单位长度,相当于将它向______(填“左”或“右”)(
个单位长度,相当于将它向______(填“左”或“右”)( 时)或将它向______(填“左”或“右”)(
时)或将它向______(填“左”或“右”)( 时)平移了
时)平移了 个单位长度,且
个单位长度,且 ,
, ,
,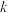 满足等式_______.
满足等式_______.19.如图,在 中,
中, ,
, 是
是 边上一点,以
边上一点,以 为圆心,
为圆心, 为半径的圆与
为半径的圆与 相交于点
相交于点 ,连接
,连接 ,且
,且 .
.

(1)求证: 是
是 的切线;
的切线;
(2)若 ,
, ,求
,求 的长.
的长.
 中,
中, ,
, 是
是 边上一点,以
边上一点,以 为圆心,
为圆心, 为半径的圆与
为半径的圆与 相交于点
相交于点 ,连接
,连接 ,且
,且 .
.
(1)求证:
 是
是 的切线;
的切线;(2)若
 ,
, ,求
,求 的长.
的长.20.某校为提高学生的综合素质,准备开设“泥塑”“绘画”“书法”“街舞”四门校本课程,为了解学生对这四门课程的选择情况(要求每名学生只能选择其中一门课程),学校从七年级学生中随机抽取部分学生进行问卷调查,根据调查结果绘制成如图所示的两幅不完整的统计图.

请你依据图中信息解答下列问题:
(1)参加此次问卷调查的学生人数是______人,在扇形统计图中,选择“泥塑”的学生所对应的扇形圆心角的度数是______;
(2)通过计算将条形统计图补充完整;
(3)若该校七年级共有 名学生,请估计七年级学生中选择“书法”课程的约有多少人?
名学生,请估计七年级学生中选择“书法”课程的约有多少人?

请你依据图中信息解答下列问题:
(1)参加此次问卷调查的学生人数是______人,在扇形统计图中,选择“泥塑”的学生所对应的扇形圆心角的度数是______;
(2)通过计算将条形统计图补充完整;
(3)若该校七年级共有
 名学生,请估计七年级学生中选择“书法”课程的约有多少人?
名学生,请估计七年级学生中选择“书法”课程的约有多少人?21.如图,小文在数学综合实践活动中,利用所学的数学知识测量居民楼的高度 ,在居民楼前方有一斜坡,坡长
,在居民楼前方有一斜坡,坡长 ,斜坡的倾斜角为
,斜坡的倾斜角为 ,
, .小文在
.小文在 点处测得楼顶端
点处测得楼顶端 的仰角为
的仰角为 ,在
,在 点处测得楼顶端
点处测得楼顶端 的仰角为
的仰角为 (点
(点 ,
, ,
, ,
, 在同一平面内).
在同一平面内).

(1)求 ,
, 两点的高度差;
两点的高度差;
(2)求居民楼的高度 .(结果精确到
.(结果精确到 ,参考数据:
,参考数据: )
)
 ,在居民楼前方有一斜坡,坡长
,在居民楼前方有一斜坡,坡长 ,斜坡的倾斜角为
,斜坡的倾斜角为 ,
, .小文在
.小文在 点处测得楼顶端
点处测得楼顶端 的仰角为
的仰角为 ,在
,在 点处测得楼顶端
点处测得楼顶端 的仰角为
的仰角为 (点
(点 ,
, ,
, ,
, 在同一平面内).
在同一平面内).
(1)求
 ,
, 两点的高度差;
两点的高度差;(2)求居民楼的高度
 .(结果精确到
.(结果精确到 ,参考数据:
,参考数据: )
)22.某公司引入一条新生产线生产A,B两种产品,其中A产品每件成本为 元,销售价格为
元,销售价格为 元,B产品每件成本为
元,B产品每件成本为 元,销售价格为
元,销售价格为 元,A,B两种产品均能在生产当月全部售出.
元,A,B两种产品均能在生产当月全部售出.
(1)第一个月该公司生产的A,B两种产品的总成本为 元,销售总利润为
元,销售总利润为 元,求这个月生产A,B两种产品各多少件?
元,求这个月生产A,B两种产品各多少件?
(2)下个月该公司计划生产A,B两种产品共 件,且使总利润不低于
件,且使总利润不低于 元,则B产品至少要生产多少件?
元,则B产品至少要生产多少件?
 元,销售价格为
元,销售价格为 元,B产品每件成本为
元,B产品每件成本为 元,销售价格为
元,销售价格为 元,A,B两种产品均能在生产当月全部售出.
元,A,B两种产品均能在生产当月全部售出.(1)第一个月该公司生产的A,B两种产品的总成本为
 元,销售总利润为
元,销售总利润为 元,求这个月生产A,B两种产品各多少件?
元,求这个月生产A,B两种产品各多少件?(2)下个月该公司计划生产A,B两种产品共
 件,且使总利润不低于
件,且使总利润不低于 元,则B产品至少要生产多少件?
元,则B产品至少要生产多少件?23.已知,四边形 是正方形,
是正方形, 绕点
绕点 旋转(
旋转( ),
), ,
, ,连接
,连接 ,
, .
.

(1)如图 ,求证:
,求证: ≌
≌ ;
;
(2)直线 与
与 相交于点
相交于点 .
.
 如图
如图 ,
, 于点
于点 ,
, 于点
于点 ,求证:四边形
,求证:四边形 是正方形;
是正方形;
 如图
如图 ,连接
,连接 ,若
,若 ,
, ,直接写出在
,直接写出在 旋转的过程中,线段
旋转的过程中,线段 长度的最小值.
长度的最小值.
 是正方形,
是正方形, 绕点
绕点 旋转(
旋转( ),
), ,
, ,连接
,连接 ,
, .
.
(1)如图
 ,求证:
,求证: ≌
≌ ;
;(2)直线
 与
与 相交于点
相交于点 .
. 如图
如图 ,
, 于点
于点 ,
, 于点
于点 ,求证:四边形
,求证:四边形 是正方形;
是正方形; 如图
如图 ,连接
,连接 ,若
,若 ,
, ,直接写出在
,直接写出在 旋转的过程中,线段
旋转的过程中,线段 长度的最小值.
长度的最小值.24.如图,已知二次函数 的图像交
的图像交 轴于点
轴于点 ,
, ,交
,交 轴于点
轴于点 .
.

(1)求这个二次函数的表达式;
(2)如图 ,点
,点 从点
从点 出发,以每秒
出发,以每秒 个单位长度的速度沿线段
个单位长度的速度沿线段 向点
向点 运动,点
运动,点 从点
从点 出发,以每秒
出发,以每秒 个单位长度的速度沿线段
个单位长度的速度沿线段 向点
向点 运动,点
运动,点 ,
, 同时出发.设运动时间为
同时出发.设运动时间为 秒(
秒( ).当
).当 为何值时,
为何值时, 的面积最大?最大面积是多少?
的面积最大?最大面积是多少?
(3)已知 是抛物线上一点,在直线
是抛物线上一点,在直线 上是否存在点
上是否存在点 ,使以
,使以 ,
, ,
, ,
, 为顶点的四边形是平行四边形?若存在,直接写出点
为顶点的四边形是平行四边形?若存在,直接写出点 坐标;若不存在,请说明理由.
坐标;若不存在,请说明理由.
 的图像交
的图像交 轴于点
轴于点 ,
, ,交
,交 轴于点
轴于点 .
.
(1)求这个二次函数的表达式;
(2)如图
 ,点
,点 从点
从点 出发,以每秒
出发,以每秒 个单位长度的速度沿线段
个单位长度的速度沿线段 向点
向点 运动,点
运动,点 从点
从点 出发,以每秒
出发,以每秒 个单位长度的速度沿线段
个单位长度的速度沿线段 向点
向点 运动,点
运动,点 ,
, 同时出发.设运动时间为
同时出发.设运动时间为 秒(
秒( ).当
).当 为何值时,
为何值时, 的面积最大?最大面积是多少?
的面积最大?最大面积是多少?(3)已知
 是抛物线上一点,在直线
是抛物线上一点,在直线 上是否存在点
上是否存在点 ,使以
,使以 ,
, ,
, ,
, 为顶点的四边形是平行四边形?若存在,直接写出点
为顶点的四边形是平行四边形?若存在,直接写出点 坐标;若不存在,请说明理由.
坐标;若不存在,请说明理由. 搜索
搜索
 难度系数:0.85
难度系数:0.85  答案解析
答案解析
 有奖纠错
有奖纠错





