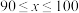全一卷
1.下列说法中,正确的是( )
A.2与 互为倒数 互为倒数 | B.2与 互为相反数 互为相反数 | C.0的相反数是0 | D.2的绝对值是 |
2.下列运算正确的是( )
A. | B. |
C. | D. |
3.一个几何体的三视图如图所示,则该几何体为( )


| A.圆柱 | B.圆锥 | C.四棱柱 | D.四棱锥 |
4.一块直角三角板按如图所示方式放置在一张长方形纸条上,若 ,则
,则 的度数为( )
的度数为( )

 ,则
,则 的度数为( )
的度数为( )
| A.28° | B.56° | C.36° | D.62° |
5.已知关于 的一元二次方程
的一元二次方程 的两根分别记为
的两根分别记为 ,
, ,若
,若 ,则
,则 的值为( )
的值为( )
 的一元二次方程
的一元二次方程 的两根分别记为
的两根分别记为 ,
, ,若
,若 ,则
,则 的值为( )
的值为( )| A.7 | B. | C.6 | D. |
6.如图,已知正六边形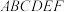 内接于半径为
内接于半径为 的
的 ,随机地往
,随机地往 内投一粒米,落在正六边形内的概率为( )
内投一粒米,落在正六边形内的概率为( )

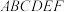 内接于半径为
内接于半径为 的
的 ,随机地往
,随机地往 内投一粒米,落在正六边形内的概率为( )
内投一粒米,落在正六边形内的概率为( )
A. | B. | C. | D.以上答案都不对 |
7.若二次函数 的图像如图所示,则一次函数
的图像如图所示,则一次函数 与反比例函数
与反比例函数 在同一坐标系内的大致图像为( )
在同一坐标系内的大致图像为( )

 的图像如图所示,则一次函数
的图像如图所示,则一次函数 与反比例函数
与反比例函数 在同一坐标系内的大致图像为( )
在同一坐标系内的大致图像为( )
A. | B. | C. | D. |
8.如图, 、
、 分别与
分别与 相切于点
相切于点 、
、 ,连接
,连接 并延长与
并延长与 交于点
交于点 、
、 ,若
,若 ,
, ,则
,则 的值为( )
的值为( )

 、
、 分别与
分别与 相切于点
相切于点 、
、 ,连接
,连接 并延长与
并延长与 交于点
交于点 、
、 ,若
,若 ,
, ,则
,则 的值为( )
的值为( )
A. | B. | C. | D. |
9.如图,在边长为2的等边三角形 的外侧作正方形
的外侧作正方形 ,过点
,过点 作
作 ,垂足为
,垂足为 ,则
,则 的长为( )
的长为( )

 的外侧作正方形
的外侧作正方形 ,过点
,过点 作
作 ,垂足为
,垂足为 ,则
,则 的长为( )
的长为( )
A. | B. | C. | D. |
10.在解决数学实际问题时,常常用到数形结合思想,比如: 的几何意义是数轴上表示数
的几何意义是数轴上表示数 的点与表示数
的点与表示数 的点的距离,
的点的距离, 的几何意义是数轴上表示数
的几何意义是数轴上表示数 的点与表示数2的点的距离.当
的点与表示数2的点的距离.当 取得最小值时,
取得最小值时, 的取值范围是( )
的取值范围是( )
 的几何意义是数轴上表示数
的几何意义是数轴上表示数 的点与表示数
的点与表示数 的点的距离,
的点的距离, 的几何意义是数轴上表示数
的几何意义是数轴上表示数 的点与表示数2的点的距离.当
的点与表示数2的点的距离.当 取得最小值时,
取得最小值时, 的取值范围是( )
的取值范围是( )A. | B. 或 或 | C. | D. |
11.有一种新冠病毒直径为0.000000012米,数0.000000012用科学记数法表示为________ .
12.分解因式:
_______ .

13.某中学在一次田径运动会上,参加女子跳高的7名运动员的成绩如下(单位:m):1.20,1.25,1.10,1.15,1.35,1.30,1.30.这组数据的中位数是_______ .
14.若 ,则
,则 的值是
的值是________ .
 ,则
,则 的值是
的值是15.如图,矩形 的对角线
的对角线 ,
, 相交于点
相交于点 ,
, //
// ,
, //
// .若
.若 ,则四边形
,则四边形 的周长是
的周长是_______ .

 的对角线
的对角线 ,
, 相交于点
相交于点 ,
, //
// ,
, //
// .若
.若 ,则四边形
,则四边形 的周长是
的周长是
16.如图,在 中,
中, ,半径为3cm的
,半径为3cm的 是
是 的内切圆,连接
的内切圆,连接 、
、 ,则图中阴影部分的面积是
,则图中阴影部分的面积是__________ cm2.(结果用含 的式子表示)
的式子表示)

 中,
中, ,半径为3cm的
,半径为3cm的 是
是 的内切圆,连接
的内切圆,连接 、
、 ,则图中阴影部分的面积是
,则图中阴影部分的面积是 的式子表示)
的式子表示)
17.如图,校园内有一株枯死的大树 ,距树12米处有一栋教学楼
,距树12米处有一栋教学楼 ,为了安全,学校决定砍伐该树,站在楼顶
,为了安全,学校决定砍伐该树,站在楼顶 处,测得点
处,测得点 的仰角为45°,点
的仰角为45°,点 的俯角为30°,小青计算后得到如下结论:①
的俯角为30°,小青计算后得到如下结论:① 米;②
米;② 米;③若直接从点
米;③若直接从点 处砍伐,树干倒向教学楼
处砍伐,树干倒向教学楼 方向会对教学楼有影响;④若第一次在距点
方向会对教学楼有影响;④若第一次在距点 的8米处的树干上砍伐,不会对教学楼
的8米处的树干上砍伐,不会对教学楼 造成危害.其中正确的是
造成危害.其中正确的是_______ .(填写序号,参考数值: ,
, )
)

 ,距树12米处有一栋教学楼
,距树12米处有一栋教学楼 ,为了安全,学校决定砍伐该树,站在楼顶
,为了安全,学校决定砍伐该树,站在楼顶 处,测得点
处,测得点 的仰角为45°,点
的仰角为45°,点 的俯角为30°,小青计算后得到如下结论:①
的俯角为30°,小青计算后得到如下结论:① 米;②
米;② 米;③若直接从点
米;③若直接从点 处砍伐,树干倒向教学楼
处砍伐,树干倒向教学楼 方向会对教学楼有影响;④若第一次在距点
方向会对教学楼有影响;④若第一次在距点 的8米处的树干上砍伐,不会对教学楼
的8米处的树干上砍伐,不会对教学楼 造成危害.其中正确的是
造成危害.其中正确的是 ,
, )
)
18.在平面直角坐标系中,将抛物线 先绕原点旋转180°,再向下平移5个单位,所得到的抛物线的顶点坐标是
先绕原点旋转180°,再向下平移5个单位,所得到的抛物线的顶点坐标是_______ .
 先绕原点旋转180°,再向下平移5个单位,所得到的抛物线的顶点坐标是
先绕原点旋转180°,再向下平移5个单位,所得到的抛物线的顶点坐标是19.如图,在平面直角坐标系中,等腰直角三角形 的斜边
的斜边 轴于点
轴于点 ,直角顶点
,直角顶点 在
在 轴上,双曲线
轴上,双曲线 经过
经过 边的中点
边的中点 ,若
,若 ,则
,则
______ .

 的斜边
的斜边 轴于点
轴于点 ,直角顶点
,直角顶点 在
在 轴上,双曲线
轴上,双曲线 经过
经过 边的中点
边的中点 ,若
,若 ,则
,则

20.如图,折叠边长为4cm的正方形纸片 ,折痕是
,折痕是 ,点
,点 落在点
落在点 处,分别延长
处,分别延长 、
、 交
交 于点
于点 、
、 ,若点
,若点 是
是 边的中点,则
边的中点,则
______ cm.

 ,折痕是
,折痕是 ,点
,点 落在点
落在点 处,分别延长
处,分别延长 、
、 交
交 于点
于点 、
、 ,若点
,若点 是
是 边的中点,则
边的中点,则

21.(1)计算: ;
;
(2)先化简,再求值: ,其中
,其中 .
.
 ;
;(2)先化简,再求值:
 ,其中
,其中 .
.22.某县教育局印发了上级主管部门的“法治和安全等知识”学习材料,某中学经过一段时间的学习,同学们都表示有了提高,为了解具体情况,综治办开展了一次全校性竞赛活动,王老师抽取了这次竞赛中部分同学的成绩,并绘制了下面不完整的统计图、表.

请根据所给的信息解答下列问题:
(1)王老师抽取了_______名学生的参赛成绩;抽取的学生的平均成绩是_______分;
(2)将条形统计图补充完整;
(3)若该校有1600名学生,请估计竞赛成绩在良好以上 的学生有多少人?
的学生有多少人?
(4)在本次竞赛中,综治办发现七(1)班、八(4)班的成绩不理想,学校要求这两个班加强学习一段时间后,再由电脑随机从A、B、C、D四套试卷中给每班派发一套试卷进行测试,请用列表或画树状图的方法求出两个班同时选中同一套试卷的概率.
参赛成绩 |
|
|
|
|
人数 | 8 |
|
| 32 |
级别 | 及格 | 中等 | 良好 | 优秀 |

请根据所给的信息解答下列问题:
(1)王老师抽取了_______名学生的参赛成绩;抽取的学生的平均成绩是_______分;
(2)将条形统计图补充完整;
(3)若该校有1600名学生,请估计竞赛成绩在良好以上
 的学生有多少人?
的学生有多少人?(4)在本次竞赛中,综治办发现七(1)班、八(4)班的成绩不理想,学校要求这两个班加强学习一段时间后,再由电脑随机从A、B、C、D四套试卷中给每班派发一套试卷进行测试,请用列表或画树状图的方法求出两个班同时选中同一套试卷的概率.
23.(1)请在图中作出 的外接圆
的外接圆 (尺规作图,保留作图痕迹,不写作法);
(尺规作图,保留作图痕迹,不写作法);

(2)如图, 是
是 的外接圆,
的外接圆, 是
是 的直径,点
的直径,点 是
是 的中点,过点
的中点,过点 的切线与
的切线与 的延长线交于点
的延长线交于点 .
.

①求证: ;
;
②若 ,
, ,求
,求 的半径.
的半径.
 的外接圆
的外接圆 (尺规作图,保留作图痕迹,不写作法);
(尺规作图,保留作图痕迹,不写作法);
(2)如图,
 是
是 的外接圆,
的外接圆, 是
是 的直径,点
的直径,点 是
是 的中点,过点
的中点,过点 的切线与
的切线与 的延长线交于点
的延长线交于点 .
.
①求证:
 ;
;②若
 ,
, ,求
,求 的半径.
的半径.24.某快递公司为了加强疫情防控需求,提高工作效率,计划购买A、B两种型号的机器人来搬运货物,已知每台A型机器人比每台B型机器人每天少搬运10吨,且A型机器人每天搬运540吨货物与B型机器人每天搬运600吨货物所需台数相同.
(1)求每台A型机器人和每台B型机器人每天分别搬运货物多少吨?
(2)每台A型机器人售价1.2万元,每台B型机器人售价2万元,该公司计划采购A、B两种型号的机器人共30台,必须满足每天搬运的货物不低于2830吨,购买金额不超过48万元.
请根据以上要求,完成如下问题:
①设购买A型机器人 台,购买总金额为
台,购买总金额为 万元,请写出
万元,请写出 与
与 的函数关系式;
的函数关系式;
②请你求出最节省的采购方案,购买总金额最低是多少万元?
(1)求每台A型机器人和每台B型机器人每天分别搬运货物多少吨?
(2)每台A型机器人售价1.2万元,每台B型机器人售价2万元,该公司计划采购A、B两种型号的机器人共30台,必须满足每天搬运的货物不低于2830吨,购买金额不超过48万元.
请根据以上要求,完成如下问题:
①设购买A型机器人
 台,购买总金额为
台,购买总金额为 万元,请写出
万元,请写出 与
与 的函数关系式;
的函数关系式;②请你求出最节省的采购方案,购买总金额最低是多少万元?
25.阅读材料:小明喜欢探究数学问题,一天杨老师给他这样一个几何问题:
如图, 和
和 都是等边三角形,点
都是等边三角形,点 在
在 上.
上.

求证:以 、
、 、
、 为边的三角形是钝角三角形.
为边的三角形是钝角三角形.
(1)【探究发现】小明通过探究发现:连接 ,根据已知条件,可以证明
,根据已知条件,可以证明 ,
, ,从而得出
,从而得出 为钝角三角形,故以
为钝角三角形,故以 、
、 、
、 为边的三角形是钝角三角形.
为边的三角形是钝角三角形.
请你根据小明的思路,写出完整的证明过程.
(2)【拓展迁移】如图,四边形 和四边形
和四边形 都是正方形,点
都是正方形,点 在
在 上.
上.

①试猜想:以 、
、 、
、 为边的三角形的形状,并说明理由.
为边的三角形的形状,并说明理由.
②若 ,试求出正方形
,试求出正方形 的面积.
的面积.
如图,
 和
和 都是等边三角形,点
都是等边三角形,点 在
在 上.
上.
求证:以
 、
、 、
、 为边的三角形是钝角三角形.
为边的三角形是钝角三角形.(1)【探究发现】小明通过探究发现:连接
 ,根据已知条件,可以证明
,根据已知条件,可以证明 ,
, ,从而得出
,从而得出 为钝角三角形,故以
为钝角三角形,故以 、
、 、
、 为边的三角形是钝角三角形.
为边的三角形是钝角三角形.请你根据小明的思路,写出完整的证明过程.
(2)【拓展迁移】如图,四边形
 和四边形
和四边形 都是正方形,点
都是正方形,点 在
在 上.
上.
①试猜想:以
 、
、 、
、 为边的三角形的形状,并说明理由.
为边的三角形的形状,并说明理由.②若
 ,试求出正方形
,试求出正方形 的面积.
的面积.26.如图,抛物线 的对称轴是直线
的对称轴是直线 ,与
,与 轴交于点
轴交于点 ,
, ,与
,与 轴交于点
轴交于点 ,连接
,连接 .
.

(1)求此抛物线的解析式;
(2)已知点 是第一象限内抛物线上的一个动点,过点
是第一象限内抛物线上的一个动点,过点 作
作 轴,垂足为点
轴,垂足为点 ,
, 交直线
交直线 于点
于点 ,是否存在这样的点
,是否存在这样的点 ,使得以
,使得以 ,
, ,
, 为顶点的三角形是等腰三角形.若存在,请求出点
为顶点的三角形是等腰三角形.若存在,请求出点 的坐标,若不存在,请说明理由;
的坐标,若不存在,请说明理由;
(3)已知点 是抛物线对称轴上的点,在坐标平面内是否存在点
是抛物线对称轴上的点,在坐标平面内是否存在点 ,使以点
,使以点 、
、 、
、 、
、 为顶点的四边形为矩形,若存在,请直接写出点
为顶点的四边形为矩形,若存在,请直接写出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
 的对称轴是直线
的对称轴是直线 ,与
,与 轴交于点
轴交于点 ,
, ,与
,与 轴交于点
轴交于点 ,连接
,连接 .
.
(1)求此抛物线的解析式;
(2)已知点
 是第一象限内抛物线上的一个动点,过点
是第一象限内抛物线上的一个动点,过点 作
作 轴,垂足为点
轴,垂足为点 ,
, 交直线
交直线 于点
于点 ,是否存在这样的点
,是否存在这样的点 ,使得以
,使得以 ,
, ,
, 为顶点的三角形是等腰三角形.若存在,请求出点
为顶点的三角形是等腰三角形.若存在,请求出点 的坐标,若不存在,请说明理由;
的坐标,若不存在,请说明理由;(3)已知点
 是抛物线对称轴上的点,在坐标平面内是否存在点
是抛物线对称轴上的点,在坐标平面内是否存在点 ,使以点
,使以点 、
、 、
、 、
、 为顶点的四边形为矩形,若存在,请直接写出点
为顶点的四边形为矩形,若存在,请直接写出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. 搜索
搜索
 难度系数:0.85
难度系数:0.85  答案解析
答案解析
 有奖纠错
有奖纠错