全一卷
1. 的相反数是( )
的相反数是( )
 的相反数是( )
的相反数是( )A. | B.37 | C. | D. |
2.如图, .若
.若 ,则
,则 的大小为( )
的大小为( )

 .若
.若 ,则
,则 的大小为( )
的大小为( )
A. | B. | C. | D. |
3.计算: ( )
( )
 ( )
( )A. | B. | C. | D. |
4.在下列条件中,能够判定 为矩形的是( )
为矩形的是( )
 为矩形的是( )
为矩形的是( )A. | B. | C. | D. |
5.如图, 是
是 的高,若
的高,若 ,
, ,则边
,则边 的长为( )
的长为( )

 是
是 的高,若
的高,若 ,
, ,则边
,则边 的长为( )
的长为( )
A. | B. | C. | D. |
6.在同一平面直角坐标系中,直线 与
与 相交于点
相交于点 ,则关于x,y的方程组
,则关于x,y的方程组 的解为( )
的解为( )
 与
与 相交于点
相交于点 ,则关于x,y的方程组
,则关于x,y的方程组 的解为( )
的解为( )A. | B. | C. | D. |
7.如图, 内接于⊙
内接于⊙ ,连接
,连接 ,则
,则 ( )
( )

 内接于⊙
内接于⊙ ,连接
,连接 ,则
,则 ( )
( )
A. | B. | C. | D. |
8.已知二次函数y=x2−2x−3的自变量x1,x2,x3对应的函数值分别为y1,y2,y3.当−1<x1<0,1<x2<2,x3>3时,y1,y2,y3三者之间的大小关系是( )
A. | B. | C. | D. |
9.计算:
______ .

10.实数a,b在数轴上对应点的位置如图所示,则a______  .(填“>”“=”或“<”)
.(填“>”“=”或“<”)

 .(填“>”“=”或“<”)
.(填“>”“=”或“<”)
11.在20世纪70年代,我国著名数学家华罗庚教授将黄金分割法作为一种“优选法”,在全国大规模推广,取得了很大成果.如图,利用黄金分割法,所做 将矩形窗框
将矩形窗框 分为上下两部分,其中E为边
分为上下两部分,其中E为边 的黄金分割点,即
的黄金分割点,即 .已知
.已知 为2米,则线段
为2米,则线段 的长为
的长为______ 米.

 将矩形窗框
将矩形窗框 分为上下两部分,其中E为边
分为上下两部分,其中E为边 的黄金分割点,即
的黄金分割点,即 .已知
.已知 为2米,则线段
为2米,则线段 的长为
的长为
12.已知点A(−2,m)在一个反比例函数的图象上,点A′与点A关于y轴对称.若点A′在正比例函数 的图象上,则这个反比例函数的表达式为
的图象上,则这个反比例函数的表达式为_______ .
 的图象上,则这个反比例函数的表达式为
的图象上,则这个反比例函数的表达式为13.如图,在菱形 中,
中, .若M、N分别是边
.若M、N分别是边 上的动点,且
上的动点,且 ,作
,作 ,垂足分别为E、F,则
,垂足分别为E、F,则 的值为
的值为______ .

 中,
中, .若M、N分别是边
.若M、N分别是边 上的动点,且
上的动点,且 ,作
,作 ,垂足分别为E、F,则
,垂足分别为E、F,则 的值为
的值为
14.计算: .
.
 .
.15.解不等式组:

16.化简: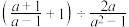 .
.
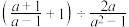 .
.17.如图,已知 是
是 的一个外角.请用尺规作图法,求作射线
的一个外角.请用尺规作图法,求作射线 ,使
,使 .(保留作图痕迹,不写作法)
.(保留作图痕迹,不写作法)

 是
是 的一个外角.请用尺规作图法,求作射线
的一个外角.请用尺规作图法,求作射线 ,使
,使 .(保留作图痕迹,不写作法)
.(保留作图痕迹,不写作法)
18.如图,在△ABC中,点D在边BC上,CD=AB,DE∥AB,∠DCE=∠A.求证:DE=BC.


19.如图, 的顶点坐标分别为
的顶点坐标分别为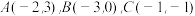 .将
.将 平移后得到
平移后得到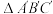 ,且点A的对应点是
,且点A的对应点是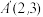 ,点B、C的对应点分别是
,点B、C的对应点分别是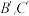 .
.
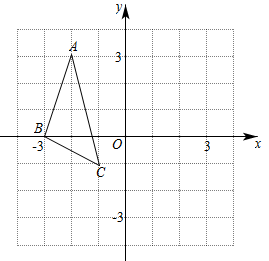
(1)点A、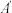 之间的距离是__________;
之间的距离是__________;
(2)请在图中画出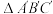 .
.
 的顶点坐标分别为
的顶点坐标分别为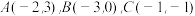 .将
.将 平移后得到
平移后得到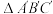 ,且点A的对应点是
,且点A的对应点是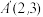 ,点B、C的对应点分别是
,点B、C的对应点分别是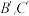 .
.
(1)点A、
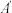 之间的距离是__________;
之间的距离是__________;(2)请在图中画出
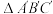 .
.20.有五个封装后外观完全相同的纸箱,且每个纸箱内各装有一个西瓜,其中,所装西瓜的重量分别为6kg,6kg,7kg,7kg,8kg.现将这五个纸箱随机摆放.
(1)若从这五个纸箱中随机选1个,则所选纸箱里西瓜的重量为6kg的概率是______;
(2)若从这五个纸箱中随机选2个,请利用列表或画树状图的方法,求所选两个纸箱里西瓜的重量之和为15kg的概率.
(1)若从这五个纸箱中随机选1个,则所选纸箱里西瓜的重量为6kg的概率是______;
(2)若从这五个纸箱中随机选2个,请利用列表或画树状图的方法,求所选两个纸箱里西瓜的重量之和为15kg的概率.
21.小明和小华利用阳光下的影子来测量一建筑物顶部旗杆的高.如图所示,在某一时刻,他们在阳光下,分别测得该建筑物OB的影长OC为16米,OA的影长OD为20米,小明的影长FG为2.4米,其中O、C、D、F、G五点在同一直线上,A、B、O三点在同一直线上,且AO⊥OD,EF⊥FG.已知小明的身高EF为1.8米,求旗杆的高AB.


22.如图,是一个“函数求值机”的示意图,其中y是x的函数.下面表格中,是通过该“函数求值机”得到的几组x与y的对应值.

根据以上信息,解答下列问题:
(1)当输入的x值为1时,输出的y值为__________;
(2)求k,b的值;
(3)当输出的y值为0时,求输入的x值.

| 输入x | … |  |  |  | 0 | 2 | … |
| 输出y | … |  |  | 2 | 6 | 16 | … |
(1)当输入的x值为1时,输出的y值为__________;
(2)求k,b的值;
(3)当输出的y值为0时,求输入的x值.
23.某校为了了解本校学生“上周内做家务劳动所用的时间”(简称“劳动时间”)情况,在本校随机调查了100名学生的“劳动时间”,并进行统计,绘制了如下统计表:
根据上述信息,解答下列问题:
(1)这100名学生的“劳动时间”的中位数落在__________组;
(2)求这100名学生的平均“劳动时间”;
(3)若该校有1200名学生,请估计在该校学生中,“劳动时间”不少于90分钟的人数.
| 组别 | “劳动时间”t/分钟 | 频数 | 组内学生的平均“劳动时间”/分钟 |
| A |  | 8 | 50 |
| B |  | 16 | 75 |
| C |  | 40 | 105 |
| D |  | 36 | 150 |
(1)这100名学生的“劳动时间”的中位数落在__________组;
(2)求这100名学生的平均“劳动时间”;
(3)若该校有1200名学生,请估计在该校学生中,“劳动时间”不少于90分钟的人数.
24.如图, 是⊙
是⊙ 的直径,
的直径, 是⊙
是⊙ 的切线,
的切线, 、
、 是⊙
是⊙ 的弦,且
的弦,且 ,垂足为E,连接
,垂足为E,连接 并延长,交
并延长,交 于点P.
于点P.

(1)求证: ;
;
(2)若⊙ 的半径
的半径 ,求线段
,求线段 的长.
的长.
 是⊙
是⊙ 的直径,
的直径, 是⊙
是⊙ 的切线,
的切线, 、
、 是⊙
是⊙ 的弦,且
的弦,且 ,垂足为E,连接
,垂足为E,连接 并延长,交
并延长,交 于点P.
于点P.
(1)求证:
 ;
;(2)若⊙
 的半径
的半径 ,求线段
,求线段 的长.
的长.25.现要修建一条隧道,其截面为抛物线型,如图所示,线段 表示水平的路面,以O为坐标原点,以
表示水平的路面,以O为坐标原点,以 所在直线为x轴,以过点O垂直于x轴的直线为y轴,建立平面直角坐标系.根据设计要求:
所在直线为x轴,以过点O垂直于x轴的直线为y轴,建立平面直角坐标系.根据设计要求: ,该抛物线的顶点P到
,该抛物线的顶点P到 的距离为
的距离为 .
.

(1)求满足设计要求的抛物线的函数表达式;
(2)现需在这一隧道内壁上安装照明灯,如图所示,即在该抛物线上的点A、B处分别安装照明灯.已知点A、B到 的距离均为
的距离均为 ,求点A、B的坐标.
,求点A、B的坐标.
 表示水平的路面,以O为坐标原点,以
表示水平的路面,以O为坐标原点,以 所在直线为x轴,以过点O垂直于x轴的直线为y轴,建立平面直角坐标系.根据设计要求:
所在直线为x轴,以过点O垂直于x轴的直线为y轴,建立平面直角坐标系.根据设计要求: ,该抛物线的顶点P到
,该抛物线的顶点P到 的距离为
的距离为 .
.
(1)求满足设计要求的抛物线的函数表达式;
(2)现需在这一隧道内壁上安装照明灯,如图所示,即在该抛物线上的点A、B处分别安装照明灯.已知点A、B到
 的距离均为
的距离均为 ,求点A、B的坐标.
,求点A、B的坐标.26.问题提出
(1)如图1, 是等边
是等边 的中线,点P在
的中线,点P在 的延长线上,且
的延长线上,且 ,则
,则 的度数为__________.
的度数为__________.
问题探究
(2)如图2,在 中,
中, .过点A作
.过点A作 ,且
,且 ,过点P作直线
,过点P作直线 ,分别交
,分别交 于点O、E,求四边形
于点O、E,求四边形 的面积.
的面积.
问题解决
(3)如图3,现有一块 型板材,
型板材, 为钝角,
为钝角, .工人师傅想用这块板材裁出一个
.工人师傅想用这块板材裁出一个 型部件,并要求
型部件,并要求 .工人师傅在这块板材上的作法如下:
.工人师傅在这块板材上的作法如下:
①以点C为圆心,以 长为半径画弧,交
长为半径画弧,交 于点D,连接
于点D,连接 ;
;
②作 的垂直平分线l,与
的垂直平分线l,与 于点E;
于点E;
③以点A为圆心,以 长为半径画弧,交直线l于点P,连接
长为半径画弧,交直线l于点P,连接 ,得
,得 .
.
请问,若按上述作法,裁得的 型部件是否符合要求?请证明你的结论.
型部件是否符合要求?请证明你的结论.

(1)如图1,
 是等边
是等边 的中线,点P在
的中线,点P在 的延长线上,且
的延长线上,且 ,则
,则 的度数为__________.
的度数为__________.问题探究
(2)如图2,在
 中,
中, .过点A作
.过点A作 ,且
,且 ,过点P作直线
,过点P作直线 ,分别交
,分别交 于点O、E,求四边形
于点O、E,求四边形 的面积.
的面积.问题解决
(3)如图3,现有一块
 型板材,
型板材, 为钝角,
为钝角, .工人师傅想用这块板材裁出一个
.工人师傅想用这块板材裁出一个 型部件,并要求
型部件,并要求 .工人师傅在这块板材上的作法如下:
.工人师傅在这块板材上的作法如下:①以点C为圆心,以
 长为半径画弧,交
长为半径画弧,交 于点D,连接
于点D,连接 ;
;②作
 的垂直平分线l,与
的垂直平分线l,与 于点E;
于点E;③以点A为圆心,以
 长为半径画弧,交直线l于点P,连接
长为半径画弧,交直线l于点P,连接 ,得
,得 .
.请问,若按上述作法,裁得的
 型部件是否符合要求?请证明你的结论.
型部件是否符合要求?请证明你的结论.
 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
