全一卷
1.5的倒数是( )
A. | B. | C.5 | D. |
2.下列各数中为无理数的是( )
A. | B.1.5 | C.0 | D. |
3.今年我市高中计划招生52300人,将数据52300用科学记数法表示是( )
A. | B. | C. | D. |
4.如图,从热气球A看一栋楼底部C的俯角是( )


A. | B. | C. | D. |
5.如图是由4个相同的小正方体组成的几何体,它的主视图是( )


A. | B. | C. | D. |
6.请你量一量如图 中
中 边上的高的长度,下列最接近的是( )
边上的高的长度,下列最接近的是( )

 中
中 边上的高的长度,下列最接近的是( )
边上的高的长度,下列最接近的是( )
A. | B. | C. | D. |
7.垃圾分类利国利民,某校宣传小组就“空矿泉水瓶应投放到哪种颜色的垃圾收集桶内”进行统计活动,他们随机采访50名学生并作好记录.以下是排乱的统计步骤:
①从扇形统计图中分析出本校学生对空矿泉水瓶投放的正确率
②整理采访记录并绘制空矿泉水瓶投放频数分布表
③绘制扇形统计图来表示空矿泉水瓶投放各收集桶所占的百分比
正确统计步骤的顺序应该是( )
①从扇形统计图中分析出本校学生对空矿泉水瓶投放的正确率
②整理采访记录并绘制空矿泉水瓶投放频数分布表
③绘制扇形统计图来表示空矿泉水瓶投放各收集桶所占的百分比
正确统计步骤的顺序应该是( )
| A.②→③→① | B.②→①→③ | C.③→①→② | D.③→②→① |
8.若x是非负整数,则表示 的值的对应点落在下图数轴上的范围是( )
的值的对应点落在下图数轴上的范围是( )

 的值的对应点落在下图数轴上的范围是( )
的值的对应点落在下图数轴上的范围是( )
| A.① | B.② | C.③ | D.①或② |
9.若顺次连接四边形 各边的中点所得的四边形是正方形,则四边形
各边的中点所得的四边形是正方形,则四边形 的两条对角线
的两条对角线 一定是( )
一定是( )
 各边的中点所得的四边形是正方形,则四边形
各边的中点所得的四边形是正方形,则四边形 的两条对角线
的两条对角线 一定是( )
一定是( )| A.互相平分 | B.互相垂直 | C.互相平分且相等 | D.互相垂直且相等 |
10.如图的电子装置中,红黑两枚跳棋开始放置在边长为2的正六边形 的顶点A处.两枚跳棋跳动规则是:红跳棋按顺时针方向1秒钟跳1个顶点,黑跳棋按逆时针方向3秒钟跳1个顶点,两枚跳棋同时跳动,经过2022秒钟后,两枚跳棋之间的距离是( )
的顶点A处.两枚跳棋跳动规则是:红跳棋按顺时针方向1秒钟跳1个顶点,黑跳棋按逆时针方向3秒钟跳1个顶点,两枚跳棋同时跳动,经过2022秒钟后,两枚跳棋之间的距离是( )

 的顶点A处.两枚跳棋跳动规则是:红跳棋按顺时针方向1秒钟跳1个顶点,黑跳棋按逆时针方向3秒钟跳1个顶点,两枚跳棋同时跳动,经过2022秒钟后,两枚跳棋之间的距离是( )
的顶点A处.两枚跳棋跳动规则是:红跳棋按顺时针方向1秒钟跳1个顶点,黑跳棋按逆时针方向3秒钟跳1个顶点,两枚跳棋同时跳动,经过2022秒钟后,两枚跳棋之间的距离是( )
| A.4 | B. | C.2 | D.0 |
11.龟兔赛跑之后,输了比赛的兔子决定和乌龟再赛一场.图中的函数图象表示了龟兔再次赛跑的过程(x表示兔子和乌龟从起点出发所走的时间, 分别表示兔子与乌龟所走的路程).下列说法
分别表示兔子与乌龟所走的路程).下列说法错误 的是( )

 分别表示兔子与乌龟所走的路程).下列说法
分别表示兔子与乌龟所走的路程).下列说法
| A.兔子和乌龟比赛路程是500米 | B.中途,兔子比乌龟多休息了35分钟 |
| C.兔子比乌龟多走了50米 | D.比赛结果,兔子比乌龟早5分钟到达终点 |
12.小嘉说:将二次函数 的图象平移或翻折后经过点
的图象平移或翻折后经过点 有4种方法:
有4种方法:
①向右平移2个单位长度 ②向右平移1个单位长度,再向下平移1个单位长度
③向下平移4个单位长度 ④沿x轴翻折,再向上平移4个单位长度
你认为小嘉说的方法中正确的个数有( )
 的图象平移或翻折后经过点
的图象平移或翻折后经过点 有4种方法:
有4种方法:①向右平移2个单位长度 ②向右平移1个单位长度,再向下平移1个单位长度
③向下平移4个单位长度 ④沿x轴翻折,再向上平移4个单位长度
你认为小嘉说的方法中正确的个数有( )
| A.1个 | B.2个 | C.3个 | D.4个 |
13.计算: .
.
 .
.14.解方程: .
.
 .
.15.问题情境:
在数学探究活动中,老师给出了如图的图形及下面三个等式:① ②
② ③
③ 若以其中两个等式作为已知条件,能否得到余下一个等式成立?
若以其中两个等式作为已知条件,能否得到余下一个等式成立?
解决方案:探究 与
与 全等.
全等.

问题解决:
(1)当选择①②作为已知条件时, 与
与 全等吗?_____________(填“全等”或“不全等”),理由是_____________;
全等吗?_____________(填“全等”或“不全等”),理由是_____________;
(2)当任意选择两个等式作为已知条件时,请用画树状图法或列表法求 的概率.
的概率.
在数学探究活动中,老师给出了如图的图形及下面三个等式:①
 ②
② ③
③ 若以其中两个等式作为已知条件,能否得到余下一个等式成立?
若以其中两个等式作为已知条件,能否得到余下一个等式成立?解决方案:探究
 与
与 全等.
全等.
问题解决:
(1)当选择①②作为已知条件时,
 与
与 全等吗?_____________(填“全等”或“不全等”),理由是_____________;
全等吗?_____________(填“全等”或“不全等”),理由是_____________;(2)当任意选择两个等式作为已知条件时,请用画树状图法或列表法求
 的概率.
的概率.16.为了加强对青少年防溺水安全教育,5月底某校开展了“远离溺水,珍爱生命”的防溺水安全知识比赛.下面是从参赛学生中随机收集到的20名学生的成绩(单位:分):
87 99 86 89 91 91 95 96 87 97
91 97 96 86 96 89 100 91 99 97
整理数据:
分析数据:
解决问题:
(1)直接写出上面表格中的a,b,c,d的值;
(2)若成绩达到95分及以上为“优秀”等级,求“优秀”等级所占的百分率;
(3)请估计该校1500名学生中成绩达到95分及以上的学生人数.
87 99 86 89 91 91 95 96 87 97
91 97 96 86 96 89 100 91 99 97
整理数据:
| 成绩(分) | 86 | 87 | 89 | 91 | 95 | 96 | 97 | 99 | 100 |
| 学生人数(人) | 2 | 2 | 2 | a | 1 | 3 | b | 2 | 1 |
| 平均数 | 众数 | 中位数 |
| 93 | c | d |
(1)直接写出上面表格中的a,b,c,d的值;
(2)若成绩达到95分及以上为“优秀”等级,求“优秀”等级所占的百分率;
(3)请估计该校1500名学生中成绩达到95分及以上的学生人数.
17.如图, 是
是 的直径,C,D都是
的直径,C,D都是 上的点,
上的点, 平分
平分 ,过点D作
,过点D作 的垂线交
的垂线交 的延长线于点E,交
的延长线于点E,交 的延长线于点F.
的延长线于点F.

(1)求证: 是
是 的切线;
的切线;
(2)若 ,
, ,求
,求 的值.
的值.
 是
是 的直径,C,D都是
的直径,C,D都是 上的点,
上的点, 平分
平分 ,过点D作
,过点D作 的垂线交
的垂线交 的延长线于点E,交
的延长线于点E,交 的延长线于点F.
的延长线于点F.
(1)求证:
 是
是 的切线;
的切线;(2)若
 ,
, ,求
,求 的值.
的值.18.我市某乡村振兴果蔬加工公司先后两次购买龙眼共21吨,第一次购买龙眼的价格为0.4万元/吨:因龙眼大量上市,价格下跌,第二次购买龙眼的价格为0.3万元/吨,两次购买龙眼共用了7万元.
(1)求两次购买龙眼各是多少吨?
(2)公司把两次购买的龙眼加工成桂圆肉和龙眼干,1吨龙眼可加工成桂圆肉0.2吨或龙眼干0.5吨,桂圆肉和龙眼干的销售价格分别是10万元/吨和3万元/吨,若全部的销售额不少于39万元,则至少需要把多少吨龙眼加工成桂圆肉?
(1)求两次购买龙眼各是多少吨?
(2)公司把两次购买的龙眼加工成桂圆肉和龙眼干,1吨龙眼可加工成桂圆肉0.2吨或龙眼干0.5吨,桂圆肉和龙眼干的销售价格分别是10万元/吨和3万元/吨,若全部的销售额不少于39万元,则至少需要把多少吨龙眼加工成桂圆肉?
19.如图,在矩形 中,
中, ,点E是
,点E是 边上的任一点(不包括端点D,C),过点A作
边上的任一点(不包括端点D,C),过点A作 交
交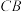 的延长线于点F,设
的延长线于点F,设 .
.

(1)求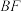 的长(用含a的代数式表示);
的长(用含a的代数式表示);
(2)连接 交
交 于点G,连接
于点G,连接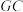 ,当
,当 时,求证:四边形
时,求证:四边形 是菱形.
是菱形.
 中,
中, ,点E是
,点E是 边上的任一点(不包括端点D,C),过点A作
边上的任一点(不包括端点D,C),过点A作 交
交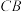 的延长线于点F,设
的延长线于点F,设 .
.
(1)求
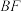 的长(用含a的代数式表示);
的长(用含a的代数式表示);(2)连接
 交
交 于点G,连接
于点G,连接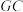 ,当
,当 时,求证:四边形
时,求证:四边形 是菱形.
是菱形.20.如图,已知抛物线: 与x轴交于点A,
与x轴交于点A, (A在B的左侧),与y轴交于点C,对称轴是直线
(A在B的左侧),与y轴交于点C,对称轴是直线 ,P是第一象限内抛物线上的任一点.
,P是第一象限内抛物线上的任一点.

(1)求抛物线的解析式;
(2)若点D为线段 的中点,则
的中点,则 能否是等边三角形?请说明理由;
能否是等边三角形?请说明理由;
(3)过点P作x轴的垂线与线段 交于点M,垂足为点H,若以P,M,C为顶点的三角形与
交于点M,垂足为点H,若以P,M,C为顶点的三角形与 相似,求点P的坐标.
相似,求点P的坐标.
 与x轴交于点A,
与x轴交于点A, (A在B的左侧),与y轴交于点C,对称轴是直线
(A在B的左侧),与y轴交于点C,对称轴是直线 ,P是第一象限内抛物线上的任一点.
,P是第一象限内抛物线上的任一点.
(1)求抛物线的解析式;
(2)若点D为线段
 的中点,则
的中点,则 能否是等边三角形?请说明理由;
能否是等边三角形?请说明理由;(3)过点P作x轴的垂线与线段
 交于点M,垂足为点H,若以P,M,C为顶点的三角形与
交于点M,垂足为点H,若以P,M,C为顶点的三角形与 相似,求点P的坐标.
相似,求点P的坐标.21.计算:
_____________ .

22.计算:
_____________ .

23.已知∠α=60°,则∠α的余角等于____ 度.
24.数学课上,老师将如图边长为1的正方形铁丝框变形成以A为圆心, 为半径的扇形(铁丝的粗细忽略不计),则所得扇形
为半径的扇形(铁丝的粗细忽略不计),则所得扇形 的面积是
的面积是_____________ .

 为半径的扇形(铁丝的粗细忽略不计),则所得扇形
为半径的扇形(铁丝的粗细忽略不计),则所得扇形 的面积是
的面积是
25.如图,在 网格中,各小正方形边长均为1,点O,A,B,C,D,E均在格点上,点O是
网格中,各小正方形边长均为1,点O,A,B,C,D,E均在格点上,点O是 的外心,在不添加其他字母的情况下,则除
的外心,在不添加其他字母的情况下,则除 外把你认为外心也是O的三角形都写出来
外把你认为外心也是O的三角形都写出来__________________________ .

 网格中,各小正方形边长均为1,点O,A,B,C,D,E均在格点上,点O是
网格中,各小正方形边长均为1,点O,A,B,C,D,E均在格点上,点O是 的外心,在不添加其他字母的情况下,则除
的外心,在不添加其他字母的情况下,则除 外把你认为外心也是O的三角形都写出来
外把你认为外心也是O的三角形都写出来
26.如图,点A在双曲线 上,点B在直线
上,点B在直线 上,A与B关于x轴对称,直线l与y轴交于点C,当四边形
上,A与B关于x轴对称,直线l与y轴交于点C,当四边形 是菱形时,有以下结论:
是菱形时,有以下结论:
① ②当
②当 时,
时,
③ ④
④
则所有正确结论的序号是_____________ .

 上,点B在直线
上,点B在直线 上,A与B关于x轴对称,直线l与y轴交于点C,当四边形
上,A与B关于x轴对称,直线l与y轴交于点C,当四边形 是菱形时,有以下结论:
是菱形时,有以下结论:①
 ②当
②当 时,
时,
③
 ④
④
则所有正确结论的序号是

 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
