全一卷
1.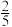 的倒数是( )
的倒数是( )
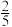 的倒数是( )
的倒数是( )A.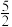 | B. | C. | D. |
2.在下列立体图形中,主视图为矩形的是( )
A. | B. | C. | D. |
3.下列命题中,假命题 是( )
A. 的绝对值是 的绝对值是 | B.对顶角相等 |
| C.平行四边形是中心对称图形 | D.如果直线 ,那么直线 ,那么直线 |
4.一元二次方程 的根的情况( )
的根的情况( )
 的根的情况( )
的根的情况( )| A.有两个相等的实数根 | B.有两个不相等的实数根 | C.没有实数根 | D.无法确定 |
5.不等式组 的解集在数轴上表示为( )
的解集在数轴上表示为( )
 的解集在数轴上表示为( )
的解集在数轴上表示为( )A. | B. | C. | D. |
6.如图,在 中,
中, 是
是 的角平分线,过点D分别作
的角平分线,过点D分别作 ,垂足分别是点E,F,则下列结论
,垂足分别是点E,F,则下列结论错误 的是( )

 中,
中, 是
是 的角平分线,过点D分别作
的角平分线,过点D分别作 ,垂足分别是点E,F,则下列结论
,垂足分别是点E,F,则下列结论
A. | B. | C. | D. |
7.已知一组数据3,3,5,6,7,8,10,那么6是这组数据的( )
| A.平均数但不是中位数 | B.平均数也是中位数 | C.众数 | D.中位数但不是平均数 |
8.下列计算错误 的是( )
A. | B. | C. | D. |
9.如图,在平面直角坐标系中,直线 与直线
与直线 相交于点A,则关于x,y的二元一次方程组
相交于点A,则关于x,y的二元一次方程组 的解是( )
的解是( )

 与直线
与直线 相交于点A,则关于x,y的二元一次方程组
相交于点A,则关于x,y的二元一次方程组 的解是( )
的解是( )
A. | B. | C. | D. |
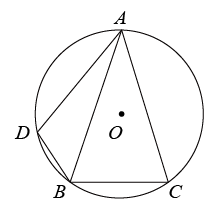
10.如图, 是
是 的外接圆,且
的外接圆,且 ,在弧AB上取点D(不与点A,B重合),连接
,在弧AB上取点D(不与点A,B重合),连接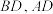 ,则
,则 的度数是( )
的度数是( )
 是
是 的外接圆,且
的外接圆,且 ,在弧AB上取点D(不与点A,B重合),连接
,在弧AB上取点D(不与点A,B重合),连接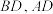 ,则
,则 的度数是( )
的度数是( )
| A.60° | B.62° | C.72° | D.73° |
11.如图,以点O为位似中心,作四边形 的位似图形
的位似图形 ﹐已知
﹐已知 ,若四边形
,若四边形 的面积是2,则四边形
的面积是2,则四边形 的面积是( )
的面积是( )

 的位似图形
的位似图形 ﹐已知
﹐已知 ,若四边形
,若四边形 的面积是2,则四边形
的面积是2,则四边形 的面积是( )
的面积是( )
| A.4 | B.6 | C.16 | D.18 |
12.如图,已知抛物线 的对称轴是
的对称轴是 ,直线
,直线 轴,且交抛物线于点
轴,且交抛物线于点 ,下列结论
,下列结论错误 的是( )

 的对称轴是
的对称轴是 ,直线
,直线 轴,且交抛物线于点
轴,且交抛物线于点 ,下列结论
,下列结论
A. | B.若实数 ,则 ,则 |
C. | D.当 时, 时, |
13.若 ,则
,则
________ .
 ,则
,则
14.在平面直角坐标系中,请写出直线 上的一个点的坐标
上的一个点的坐标________ .
 上的一个点的坐标
上的一个点的坐标15.一元二次方程 的根是
的根是_________ .
 的根是
的根是16.如图,在 中,
中, ,点D,E分别是
,点D,E分别是 边上的中点,连接
边上的中点,连接 .如果
.如果 ,
, ,那么
,那么 的长是
的长是_______ m.

 中,
中, ,点D,E分别是
,点D,E分别是 边上的中点,连接
边上的中点,连接 .如果
.如果 ,
, ,那么
,那么 的长是
的长是
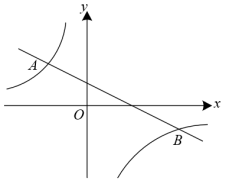
17.如图,在平面直角坐标系中,一次函数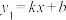 的图象与反比例函数
的图象与反比例函数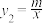 的图象交于点
的图象交于点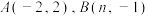 .当
.当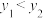 时,x的取值范围是
时,x的取值范围是_________ .
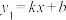 的图象与反比例函数
的图象与反比例函数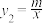 的图象交于点
的图象交于点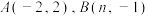 .当
.当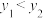 时,x的取值范围是
时,x的取值范围是
18.如图,四边形 是
是 的内接正四边形,分别以点A,O为圆心,取大于
的内接正四边形,分别以点A,O为圆心,取大于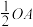 的定长为半径画弧,两弧相交于点M,N,作直线MN,交
的定长为半径画弧,两弧相交于点M,N,作直线MN,交 于点E,F.若
于点E,F.若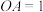 ,则
,则 ,
, 所围成的阴影部分面积为
所围成的阴影部分面积为_______ .

 是
是 的内接正四边形,分别以点A,O为圆心,取大于
的内接正四边形,分别以点A,O为圆心,取大于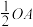 的定长为半径画弧,两弧相交于点M,N,作直线MN,交
的定长为半径画弧,两弧相交于点M,N,作直线MN,交 于点E,F.若
于点E,F.若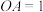 ,则
,则 ,
, 所围成的阴影部分面积为
所围成的阴影部分面积为
19.(1)计算:
(2)化简: .
.

(2)化简:
 .
.20.解方程:

21.如图,在 中,E,G,H,F分别是
中,E,G,H,F分别是 上的点,且
上的点,且 .求证:
.求证: .
.

 中,E,G,H,F分别是
中,E,G,H,F分别是 上的点,且
上的点,且 .求证:
.求证: .
.
22.某校团委为了解学生关注“2022年北京冬奥会”情况,以随机抽样的方式对学生进行问卷调查,学生只选择一个运动项目作为最关注项目,把调查结果分为“滑雪”“滑冰”“冰球”“冰壶”“其他”五类,绘制成统计图①和图②.


(1)本次抽样调查的学生人数共_______人;
(2)将图①补充完整;
(3)在这次抽样的学生中,滑冰挑选了甲,乙,丙,丁四名学生中随机抽取2名进行“爱我北京冬奥”主题演讲.请用画树状图法或列表法求出抽中两名学生分别是甲和乙的概率.


(1)本次抽样调查的学生人数共_______人;
(2)将图①补充完整;
(3)在这次抽样的学生中,滑冰挑选了甲,乙,丙,丁四名学生中随机抽取2名进行“爱我北京冬奥”主题演讲.请用画树状图法或列表法求出抽中两名学生分别是甲和乙的概率.
23.今年,我国“巅峰使命”2022珠峰科考团对珠穆朗玛峰进行综合科学考察,搭建了世界最高海拔的自动气象站,还通过释放气球方式进行了高空探测.某学校兴趣小组开展实践活动,通过观测数据,计算气球升空的高度AB.如图,在平面内,点B,C,D在同一直线上, 垂足为点B,
垂足为点B, ,
, ,
, ,求AB的高度.(精确到
,求AB的高度.(精确到 )(参考数据:
)(参考数据: ﹐
﹐ ﹐
﹐ ,
, )
)

 垂足为点B,
垂足为点B, ,
, ,
, ,求AB的高度.(精确到
,求AB的高度.(精确到 )(参考数据:
)(参考数据: ﹐
﹐ ﹐
﹐ ,
, )
)
24.梧州市地处亚热带,盛产龙眼.新鲜龙眼的保质期短,若加工成龙眼干(又叫带壳圆肉)则有利于较长时间保存.已知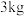 的新鲜龙眼在无损耗的情况下可以加工成
的新鲜龙眼在无损耗的情况下可以加工成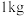 的龙眼干.
的龙眼干.
(1)若新鲜龙眼售价为12元/kg,在无损耗的情况下加工成龙眼干,使龙眼干的销售收益不低于新鲜龙眼的销售收益,则龙眼干的售价应不低于多少元/kg?
(2)在实践中,小苏发现当地在加工龙眼干的过程中新鲜龙眼有6%的损耗,为确保果农的利益,龙眼干的销售收益应不低于新鲜龙眼的销售收益,此时龙眼干的定价取最低整数价格.市场调查还发现,新鲜龙眼以12元/kg最多能卖出 ,超出部分平均售价是5元/kg,可售完.果农们都以这种方式出售新鲜龙眼.设某果农有
,超出部分平均售价是5元/kg,可售完.果农们都以这种方式出售新鲜龙眼.设某果农有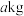 新鲜龙眼,他全部加工成龙眼干销售获得的收益与全部以新鲜龙眼销售获得的收益之差为w元,请写出w与a的函数关系式.
新鲜龙眼,他全部加工成龙眼干销售获得的收益与全部以新鲜龙眼销售获得的收益之差为w元,请写出w与a的函数关系式.
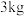 的新鲜龙眼在无损耗的情况下可以加工成
的新鲜龙眼在无损耗的情况下可以加工成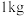 的龙眼干.
的龙眼干.(1)若新鲜龙眼售价为12元/kg,在无损耗的情况下加工成龙眼干,使龙眼干的销售收益不低于新鲜龙眼的销售收益,则龙眼干的售价应不低于多少元/kg?
(2)在实践中,小苏发现当地在加工龙眼干的过程中新鲜龙眼有6%的损耗,为确保果农的利益,龙眼干的销售收益应不低于新鲜龙眼的销售收益,此时龙眼干的定价取最低整数价格.市场调查还发现,新鲜龙眼以12元/kg最多能卖出
 ,超出部分平均售价是5元/kg,可售完.果农们都以这种方式出售新鲜龙眼.设某果农有
,超出部分平均售价是5元/kg,可售完.果农们都以这种方式出售新鲜龙眼.设某果农有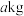 新鲜龙眼,他全部加工成龙眼干销售获得的收益与全部以新鲜龙眼销售获得的收益之差为w元,请写出w与a的函数关系式.
新鲜龙眼,他全部加工成龙眼干销售获得的收益与全部以新鲜龙眼销售获得的收益之差为w元,请写出w与a的函数关系式.25.如图,在平面直角坐标系中,直线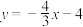 分别与x,y轴交于点A,B,抛物线
分别与x,y轴交于点A,B,抛物线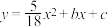 恰好经过这两点.
恰好经过这两点.
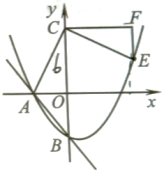
(1)求此抛物线的解析式;
(2)若点C的坐标是 ,将
,将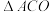 绕着点C逆时针旋转90°得到
绕着点C逆时针旋转90°得到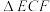 ,点A的对应点是点E.
,点A的对应点是点E.
①写出点E的坐标,并判断点E是否在此抛物线上;
②若点P是y轴上的任一点,求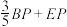 取最小值时,点P的坐标.
取最小值时,点P的坐标.
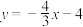 分别与x,y轴交于点A,B,抛物线
分别与x,y轴交于点A,B,抛物线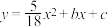 恰好经过这两点.
恰好经过这两点.
(1)求此抛物线的解析式;
(2)若点C的坐标是
 ,将
,将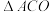 绕着点C逆时针旋转90°得到
绕着点C逆时针旋转90°得到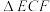 ,点A的对应点是点E.
,点A的对应点是点E.①写出点E的坐标,并判断点E是否在此抛物线上;
②若点P是y轴上的任一点,求
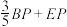 取最小值时,点P的坐标.
取最小值时,点P的坐标.26.如图,以AB为直径的半圆中,点O为圆心,点C在圆上,过点C作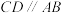 ,且
,且 .连接AD,分别交
.连接AD,分别交 于点E,F,与
于点E,F,与 交于点G,若
交于点G,若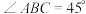 .
.

(1)求证:① ;
;
②CD是 的切线.
的切线.
(2)求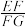 的值.
的值.
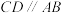 ,且
,且 .连接AD,分别交
.连接AD,分别交 于点E,F,与
于点E,F,与 交于点G,若
交于点G,若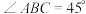 .
.
(1)求证:①
 ;
; ②CD是
 的切线.
的切线.(2)求
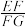 的值.
的值. 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
