全一卷
1.剪纸是我国古老的民间艺术,下列四个剪纸图案为轴对称图形的是( )
A. | B. |
C. | D. |
2.下列各数为负分数的是( )
| A.-1 | B.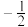 | C.0 | D. |
3.如图所示的几何体,其左视图是( )


A. | B. |
C. | D. |
4.2021年3月5 日,李克强总理在政府工作报告中指出,我国脱贫攻坚成果举世瞩目,5575万农村贫困人口实现脱贫.5575万=55750000,用科学记数法将55750000表示为( )
A. | B. | C. | D. |
5.如图,将线段 先绕原点
先绕原点 按逆时针方向旋转
按逆时针方向旋转 ,再向下平移4个单位,得到线段
,再向下平移4个单位,得到线段 ,则点
,则点 的对应点
的对应点 的坐标是( )
的坐标是( )

 先绕原点
先绕原点 按逆时针方向旋转
按逆时针方向旋转 ,再向下平移4个单位,得到线段
,再向下平移4个单位,得到线段 ,则点
,则点 的对应点
的对应点 的坐标是( )
的坐标是( )
A. | B. | C. | D. |
6.如图, 是
是 的直径,点
的直径,点 ,
, 在
在 上,点
上,点 是
是 的中点,过点
的中点,过点 画
画 的切线,交
的切线,交 的延长线于点
的延长线于点 ,连接
,连接 .若
.若 ,则
,则 的度数为( )
的度数为( )

 是
是 的直径,点
的直径,点 ,
, 在
在 上,点
上,点 是
是 的中点,过点
的中点,过点 画
画 的切线,交
的切线,交 的延长线于点
的延长线于点 ,连接
,连接 .若
.若 ,则
,则 的度数为( )
的度数为( )
A. | B. | C. | D. |
7.如图,在四边形纸片 中,
中, ,
, ,
, .将纸片折叠,使点
.将纸片折叠,使点 落在
落在 边上的点
边上的点 处,折痕为
处,折痕为 .若
.若 ,则
,则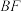 的长为( )
的长为( )

 中,
中, ,
, ,
, .将纸片折叠,使点
.将纸片折叠,使点 落在
落在 边上的点
边上的点 处,折痕为
处,折痕为 .若
.若 ,则
,则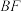 的长为( )
的长为( )
| A.5 | B. | C. | D. |
8.已知反比例函数 的图象如图所示,则一次函数
的图象如图所示,则一次函数 和二次函数
和二次函数 在同一直角坐标系中的图象可能是( )
在同一直角坐标系中的图象可能是( )

 的图象如图所示,则一次函数
的图象如图所示,则一次函数 和二次函数
和二次函数 在同一直角坐标系中的图象可能是( )
在同一直角坐标系中的图象可能是( )
A. | B. |
C. | D. |
9.计算:
__________ .

10.在一个不透明的袋中装有若干个红球和4个黑球,每个球除颜色外完全相同.摇匀后从中摸出一个球,记下颜色后再放回袋中.不断重复这一过程,共摸球100次.其中有40次摸到黑球,估计袋中红球的个数是__________ .
11.列车从甲地驶往乙地.行完全程所需的时间 与行驶的平均速度
与行驶的平均速度 之间的反比例函数关系如图所示.若列车要在
之间的反比例函数关系如图所示.若列车要在 内到达,则速度至少需要提高到
内到达,则速度至少需要提高到__________  .
.

 与行驶的平均速度
与行驶的平均速度 之间的反比例函数关系如图所示.若列车要在
之间的反比例函数关系如图所示.若列车要在 内到达,则速度至少需要提高到
内到达,则速度至少需要提高到 .
.
12.已知甲、乙两队员射击的成绩如图,设甲、乙两队员射击成绩的方差分别为 、
、 ,则
,则
___  .(填“
.(填“ ”、“
”、“ ”、“
”、“ ”)
”)

 、
、 ,则
,则
 .(填“
.(填“ ”、“
”、“ ”、“
”、“ ”)
”)
13.如图,正方形 内接于
内接于 ,
, ,
,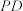 分别与
分别与 相切于点
相切于点 和点
和点 ,
,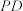 的延长线与
的延长线与 的延长线交于点
的延长线交于点 .已知
.已知 ,则图中阴影部分的面积为
,则图中阴影部分的面积为___________ .

 内接于
内接于 ,
, ,
,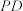 分别与
分别与 相切于点
相切于点 和点
和点 ,
,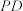 的延长线与
的延长线与 的延长线交于点
的延长线交于点 .已知
.已知 ,则图中阴影部分的面积为
,则图中阴影部分的面积为
14.已知正方形 的边长为3,
的边长为3, 为
为 上一点,连接
上一点,连接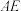 并延长,交
并延长,交 的延长线于点
的延长线于点 ,过点
,过点 作
作 ,交
,交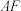 于点
于点 ,交
,交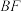 于点
于点 ,
, 为
为 的中点,
的中点, 为
为 上一动点,分别连接
上一动点,分别连接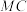 ,
, .若
.若 ,则
,则 的最小值为
的最小值为__________ .

 的边长为3,
的边长为3, 为
为 上一点,连接
上一点,连接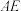 并延长,交
并延长,交 的延长线于点
的延长线于点 ,过点
,过点 作
作 ,交
,交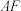 于点
于点 ,交
,交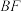 于点
于点 ,
, 为
为 的中点,
的中点, 为
为 上一动点,分别连接
上一动点,分别连接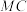 ,
, .若
.若 ,则
,则 的最小值为
的最小值为
15.已知: 及其一边上的两点
及其一边上的两点 ,
, .
.
求作: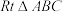 ,使
,使 ,且点
,且点 在
在 内部,
内部, .
.

 及其一边上的两点
及其一边上的两点 ,
, .
.求作:
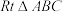 ,使
,使 ,且点
,且点 在
在 内部,
内部, .
.
16.(1)计算: ;
;
(2)解不等式组: ,并写出它的整数解.
,并写出它的整数解.
 ;
;(2)解不等式组:
 ,并写出它的整数解.
,并写出它的整数解.17.为践行青岛市中小学生“十个一”行动,某校举行文艺表演,小静和小丽想合唱一首歌.小静想唱《红旗飘飘》,而小丽想唱《大海啊,故乡》.她们想通过做游戏的方式来决定合唱哪一首歌,于是一起设计了一个游戏:下面是两个可以自由转动的转盘,每个转盘被分成面积相等的几个扇形.同时转动两个转盘,若两个指针指向的数字之积小于4,则合唱《大海啊,故乡》,否则合唱《红旗飘飘》;若指针刚好落在分割线上,则需要重新转动转盘.请用列表或画树状图的方法说明这个游戏是否公平.


18.某校数学社团开展“探索生活中的数学”研学活动,准备测量一栋大楼 的高度.如图所示,其中观景平台斜坡
的高度.如图所示,其中观景平台斜坡 的长是20米,坡角为
的长是20米,坡角为 ,斜坡
,斜坡 底部
底部 与大楼底端
与大楼底端 的距离
的距离 为74米,与地面
为74米,与地面 垂直的路灯
垂直的路灯 的高度是3米,从楼顶
的高度是3米,从楼顶 测得路灯
测得路灯 项端
项端 处的俯角是
处的俯角是 .试求大楼
.试求大楼 的高度.
的高度.
(参考数据: ,
, ,
, ,
, ,
, ,
, )
)

 的高度.如图所示,其中观景平台斜坡
的高度.如图所示,其中观景平台斜坡 的长是20米,坡角为
的长是20米,坡角为 ,斜坡
,斜坡 底部
底部 与大楼底端
与大楼底端 的距离
的距离 为74米,与地面
为74米,与地面 垂直的路灯
垂直的路灯 的高度是3米,从楼顶
的高度是3米,从楼顶 测得路灯
测得路灯 项端
项端 处的俯角是
处的俯角是 .试求大楼
.试求大楼 的高度.
的高度.(参考数据:
 ,
, ,
, ,
, ,
, ,
, )
)
19.在中国共产党成立一百周年之际,某校举行了以“童心向党”为主题的知识竞赛活动.发现该校全体学生的竞赛成绩(百分制)均不低于60分,现从中随机抽取 名学生的竞赛成绩进行整理和分析(成绩得分用
名学生的竞赛成绩进行整理和分析(成绩得分用 表示,共分成四组),并绘制成如下的竞赛成绩分组统计表和扇形统计图.其中“
表示,共分成四组),并绘制成如下的竞赛成绩分组统计表和扇形统计图.其中“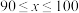 ”这组的数据如下:
”这组的数据如下:
90,92,93,95,95,96,96,96,97,100.
竞赛成绩分组统计表

请根据以上信息,解答下列问题:
(1) __________;
__________;
(2)“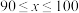 ”这组数据的众数是__________分;
”这组数据的众数是__________分;
(3)随机抽取的这 名学生竞赛成绩的平均分是___________分;
名学生竞赛成绩的平均分是___________分;
(4)若学生竞赛成绩达到96分以上(含96分)获奖,请你估计全校1200名学生中获奖的人数.
 名学生的竞赛成绩进行整理和分析(成绩得分用
名学生的竞赛成绩进行整理和分析(成绩得分用 表示,共分成四组),并绘制成如下的竞赛成绩分组统计表和扇形统计图.其中“
表示,共分成四组),并绘制成如下的竞赛成绩分组统计表和扇形统计图.其中“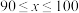 ”这组的数据如下:
”这组的数据如下:90,92,93,95,95,96,96,96,97,100.
竞赛成绩分组统计表
| 组别 | 竞赛成绩分组 | 频数 | 平均分 |
| 1 |  | 8 | 65 |
| 2 |  |  | 75 |
| 3 |  |  | 88 |
| 4 | 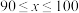 | 10 | 95 |

请根据以上信息,解答下列问题:
(1)
 __________;
__________;(2)“
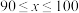 ”这组数据的众数是__________分;
”这组数据的众数是__________分;(3)随机抽取的这
 名学生竞赛成绩的平均分是___________分;
名学生竞赛成绩的平均分是___________分;(4)若学生竞赛成绩达到96分以上(含96分)获奖,请你估计全校1200名学生中获奖的人数.
20.某超市经销甲、乙两种品牌的洗衣液,进货时发现,甲品牌洗衣液每瓶的进价比乙品牌高6元,用1800元购进甲品牌洗衣液的数量是用1800元购进乙品牌洗衣液数量的 .销售时,甲品牌洗衣液的售价为36元/瓶,乙品牌洗衣液的售价为28元/瓶.
.销售时,甲品牌洗衣液的售价为36元/瓶,乙品牌洗衣液的售价为28元/瓶.
(1)求两种品牌洗衣液的进价;
(2)若超市需要购进甲、乙两种品牌的洗衣液共120瓶,且购进两种洗衣液的总成本不超过3120元,超市应购进甲、乙两种品牌洗衣液各多少瓶,才能在两种洗衣液完全售出后所获利润最大?最大利润是多少元?
 .销售时,甲品牌洗衣液的售价为36元/瓶,乙品牌洗衣液的售价为28元/瓶.
.销售时,甲品牌洗衣液的售价为36元/瓶,乙品牌洗衣液的售价为28元/瓶.(1)求两种品牌洗衣液的进价;
(2)若超市需要购进甲、乙两种品牌的洗衣液共120瓶,且购进两种洗衣液的总成本不超过3120元,超市应购进甲、乙两种品牌洗衣液各多少瓶,才能在两种洗衣液完全售出后所获利润最大?最大利润是多少元?
21.如图,在 中,
中, 为
为 边的中点,连接
边的中点,连接 并延长,交
并延长,交 的延长线于点
的延长线于点 ,延长
,延长 至点
至点 ,使
,使 ,分别连接
,分别连接 ,
, ,
, .
.

(1)求证: ;
;
(2)当 平分
平分 时,四边形
时,四边形 是什么特殊四边形?请说明理由.
是什么特殊四边形?请说明理由.
 中,
中, 为
为 边的中点,连接
边的中点,连接 并延长,交
并延长,交 的延长线于点
的延长线于点 ,延长
,延长 至点
至点 ,使
,使 ,分别连接
,分别连接 ,
, ,
, .
.
(1)求证:
 ;
;(2)当
 平分
平分 时,四边形
时,四边形 是什么特殊四边形?请说明理由.
是什么特殊四边形?请说明理由.22.科研人员为了研究弹射器的某项性能,利用无人机测量小钢球竖直向上运动的相关数据.无人机上升到离地面30米处开始保持匀速竖直上升,此时,在地面用弹射器(高度不计)竖直向上弹射一个小钢球(忽路空气阻力),在1秒时,它们距离地面都是35米,在6秒时,它们距离地面的高度也相同.其中无人机离地面高度 (米)与小钢球运动时间
(米)与小钢球运动时间 (秒)之间的函数关系如图所示;小钢球离地面高度
(秒)之间的函数关系如图所示;小钢球离地面高度 (米)与它的运动时间
(米)与它的运动时间 (秒)之间的函数关系如图中抛物线所示.
(秒)之间的函数关系如图中抛物线所示.

(1)直接写出 与
与 之间的函数关系式;
之间的函数关系式;
(2)求出 与
与 之间的函数关系式;
之间的函数关系式;
(3)小钢球弹射1秒后直至落地时,小钢球和无人机的高度差最大是多少米?
 (米)与小钢球运动时间
(米)与小钢球运动时间 (秒)之间的函数关系如图所示;小钢球离地面高度
(秒)之间的函数关系如图所示;小钢球离地面高度 (米)与它的运动时间
(米)与它的运动时间 (秒)之间的函数关系如图中抛物线所示.
(秒)之间的函数关系如图中抛物线所示.
(1)直接写出
 与
与 之间的函数关系式;
之间的函数关系式;(2)求出
 与
与 之间的函数关系式;
之间的函数关系式;(3)小钢球弹射1秒后直至落地时,小钢球和无人机的高度差最大是多少米?
23.问题提出:
最长边长为128的整数边三角形有多少个?(整数边三角形是指三边长度都是整数的三角形.)
问题探究:
为了探究规律,我们先从最简单的情形入手,从中找到解决问题的方法,最后得出一般性的结论.
(1)如表①,最长边长为1的整数边三角形,显然,最短边长是1,第三边长也是1.按照(最长边长,最短边长,第三边长)的形式记为 ,有1个,所以总共有
,有1个,所以总共有 个整数边三角形.
个整数边三角形.
表①
(2)如表②,最长边长为2的整数边三角形,最短边长是1或2.根据三角形任意两边之和大于第三边,当最短边长为1时,第三边长只能是2,记为 ,有1个;当最短边长为2时,显然第三边长也是2,记为
,有1个;当最短边长为2时,显然第三边长也是2,记为 ,有1个,所以总共有
,有1个,所以总共有 个整数边三角形.
个整数边三角形.
表②
(3)下面在表③中总结最长边长为3的整数边三角形个数情况:
表③
(4)下面在表④中总结最长边长为4的整数边三角形个数情况:
表④
(5)请在表⑤中总结最长边长为5的整数边三角形个数情况并填空:
表⑤
问题解决:
(1)最长边长为6的整数边三角形有___________个.
(2)在整数边三角形中,设最长边长为 ,总结上述探究过程,当
,总结上述探究过程,当 为奇数或
为奇数或 为偶数时,整数边三角形个数的规律一样吗?请写出最长边长为
为偶数时,整数边三角形个数的规律一样吗?请写出最长边长为 的整数边三角形的个数.
的整数边三角形的个数.
(3)最长边长为128的整数边三角形有__________个.
拓展延伸:
在直三棱柱中,若所有棱长均为整数,则最长棱长为9的直三棱柱有___________个.
最长边长为128的整数边三角形有多少个?(整数边三角形是指三边长度都是整数的三角形.)
问题探究:
为了探究规律,我们先从最简单的情形入手,从中找到解决问题的方法,最后得出一般性的结论.
(1)如表①,最长边长为1的整数边三角形,显然,最短边长是1,第三边长也是1.按照(最长边长,最短边长,第三边长)的形式记为
 ,有1个,所以总共有
,有1个,所以总共有 个整数边三角形.
个整数边三角形.表①
| 最长边长 | 最短边长 | (最长边长,最短边长,第三边长) | 整数边三角形个数 | 计算方法 | 算式 |
| 1 | 1 |  | 1 | 1个1 |  |
(2)如表②,最长边长为2的整数边三角形,最短边长是1或2.根据三角形任意两边之和大于第三边,当最短边长为1时,第三边长只能是2,记为
 ,有1个;当最短边长为2时,显然第三边长也是2,记为
,有1个;当最短边长为2时,显然第三边长也是2,记为 ,有1个,所以总共有
,有1个,所以总共有 个整数边三角形.
个整数边三角形.表②
| 最长边长 | 最短边长 | (最长边长,最短边长,第三边长) | 整数边三角形个数 | 计算方法 | 算式 |
| 2 | 1 |  | 1 | 2个1 |  |
| 2 |  | 1 |
(3)下面在表③中总结最长边长为3的整数边三角形个数情况:
表③
| 最长边长 | 最短边长 | (最长边长,最短边长,第三边长) | 整数边三角形个数 | 计算方法 | 算式 |
| 3 | 1 |  | 1 | 2个2 |  |
| 2 |  , , | 2 | |||
| 3 |  | 1 |
(4)下面在表④中总结最长边长为4的整数边三角形个数情况:
表④
| 最长边长 | 最短边长 | (最长边长,最短边长,第三边长) | 整数边三角形个数 | 计算方法 | 算式 |
| 4 | 1 |  | 1 | 3个2 |  |
| 2 |  , , | 2 | |||
| 3 |  , , | 2 | |||
| 4 |  | 1 |
(5)请在表⑤中总结最长边长为5的整数边三角形个数情况并填空:
表⑤
| 最长边长 | 最短边长 | (最长边长,最短边长,第三边长) | 整数边三角形个数 | 计算方法 | 算式 |
| 5 | 1 |  | 1 | ___ | ___ |
| 2 |  , , | 2 | |||
| 3 | _______ | _____ | |||
| 4 |  , , | 2 | |||
| 5 |  | 1 |
问题解决:
(1)最长边长为6的整数边三角形有___________个.
(2)在整数边三角形中,设最长边长为
 ,总结上述探究过程,当
,总结上述探究过程,当 为奇数或
为奇数或 为偶数时,整数边三角形个数的规律一样吗?请写出最长边长为
为偶数时,整数边三角形个数的规律一样吗?请写出最长边长为 的整数边三角形的个数.
的整数边三角形的个数.(3)最长边长为128的整数边三角形有__________个.
拓展延伸:
在直三棱柱中,若所有棱长均为整数,则最长棱长为9的直三棱柱有___________个.
24.已知:如图,在矩形 和等腰
和等腰 中,
中, ,
, ,
, .点
.点 从点
从点 出发,沿
出发,沿 方向匀速运动.速度为
方向匀速运动.速度为 ;同时,点
;同时,点 从点
从点 出发,沿
出发,沿 方向匀速运动,速度为
方向匀速运动,速度为 .过点
.过点 作
作 ,交
,交 于点
于点 ,交
,交 于点
于点 ,过点
,过点 作
作 ,交
,交 于点
于点 .分别连接
.分别连接 ,
, ,设运动时间为
,设运动时间为 .
.
解答下列问题:

(1)当 时,求
时,求 的值;
的值;
(2)设五边形 的面积为
的面积为 ,求
,求 与
与 之间的函数关系式;
之间的函数关系式;
(3)当 时,求
时,求 的值;
的值;
(4)若 与
与 相交于点
相交于点 ,分别连接
,分别连接 和
和 .在运动过程中,是否存在某一时刻
.在运动过程中,是否存在某一时刻 ,使
,使 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 和等腰
和等腰 中,
中, ,
, ,
, .点
.点 从点
从点 出发,沿
出发,沿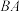 方向匀速运动.速度为
方向匀速运动.速度为 ;同时,点
;同时,点 从点
从点 出发,沿
出发,沿 方向匀速运动,速度为
方向匀速运动,速度为 .过点
.过点 作
作 ,交
,交 于点
于点 ,交
,交 于点
于点 ,过点
,过点 作
作 ,交
,交 于点
于点 .分别连接
.分别连接 ,
, ,设运动时间为
,设运动时间为 .
.解答下列问题:

(1)当
 时,求
时,求 的值;
的值;(2)设五边形
 的面积为
的面积为 ,求
,求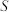 与
与 之间的函数关系式;
之间的函数关系式;(3)当
 时,求
时,求 的值;
的值;(4)若
 与
与 相交于点
相交于点 ,分别连接
,分别连接 和
和 .在运动过程中,是否存在某一时刻
.在运动过程中,是否存在某一时刻 ,使
,使 ?若存在,求出
?若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由. 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
