全一卷
1.-2021的绝对值是( )
A. | B. | C.2021 | D. |
2.从2021年5月26日在南昌召开的第十二届中国卫星导航年会上获悉,至2020年,我国卫星导航产业总值突破4000亿元,年均增长 以上,其中4000亿用科学记数法表示为( )
以上,其中4000亿用科学记数法表示为( )
 以上,其中4000亿用科学记数法表示为( )
以上,其中4000亿用科学记数法表示为( )A. | B. | C. | D. |
3.下列几何体中,其主视图、左视图和俯视图完全相同的是( )
A. | B. |
C. | D. |
4.某中学七(1)班的6位同学在课间体育活动时进行一分钟跳绳比赛,成绩(单位:个)如下:122,146,134,146,152,121.这组数据的众数和中位数分别是( )
| A.152,134 | B.146,146 | C.146,140 | D.152,140 |
5.如图, ,
, ,
, ,则
,则 的度数为( )
的度数为( )

 ,
, ,
, ,则
,则 的度数为( )
的度数为( )
A. | B. | C. | D. |
6.下列计算正确的是( )
A. | B. |
C. | D. |
7.在同一时刻,物体的高度与它在阳光下的影长成正比.在某一时刻,有人测得一高为 的竹竿的影长为
的竹竿的影长为 ,某一高楼的影长为
,某一高楼的影长为 ,那么这幢高楼的高度是( )
,那么这幢高楼的高度是( )
 的竹竿的影长为
的竹竿的影长为 ,某一高楼的影长为
,某一高楼的影长为 ,那么这幢高楼的高度是( )
,那么这幢高楼的高度是( )A. | B. | C. | D. |
8.函数 中,自变量
中,自变量 的取值范围是( )
的取值范围是( )
 中,自变量
中,自变量 的取值范围是( )
的取值范围是( )A. | B. 且 且 | C. | D. 且 且 |
9.如图, 是
是 的外接圆,
的外接圆, ,若
,若 的半径
的半径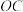 为2,则弦
为2,则弦 的长为( )
的长为( )

 是
是 的外接圆,
的外接圆, ,若
,若 的半径
的半径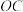 为2,则弦
为2,则弦 的长为( )
的长为( )
| A.4 | B.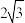 | C.3 | D. |
10.某商品经过两次降价,售价由原来的每件25元降到每件16元,已知两次降价的百分率相同,则每次降价的百分率为( )
A. | B. | C. | D. |
11.如图,在边长为 的等边
的等边 中,分别取
中,分别取 三边的中点
三边的中点 ,
, ,
, ,得△
,得△ ;再分别取△
;再分别取△ 三边的中点
三边的中点 ,
, ,
, ,得△
,得△ ;这样依次下去
;这样依次下去 ,经过第2021次操作后得△
,经过第2021次操作后得△ ,则△
,则△ 的面积为( )
的面积为( )

 的等边
的等边 中,分别取
中,分别取 三边的中点
三边的中点 ,
, ,
, ,得△
,得△ ;再分别取△
;再分别取△ 三边的中点
三边的中点 ,
, ,
, ,得△
,得△ ;这样依次下去
;这样依次下去 ,经过第2021次操作后得△
,经过第2021次操作后得△ ,则△
,则△ 的面积为( )
的面积为( )
A. | B. | C. | D. |
12.如图,菱形 的顶点分别在反比例函数
的顶点分别在反比例函数 和
和 的图象上,若
的图象上,若 ,则
,则 的值为( )
的值为( )

 的顶点分别在反比例函数
的顶点分别在反比例函数 和
和 的图象上,若
的图象上,若 ,则
,则 的值为( )
的值为( )
A. | B. | C. | D. |
13.分解因式:
__ .

14.有背面完全相同,正面分别画有等腰三角形、平行四边形、矩形、菱形、等腰梯形的卡片5张,现正面朝下放置在桌面上,将其混合后,并从中随机抽取一张,则抽中正面的图形一定是轴对称图形的卡片的概率为 __ .
15.若关于x的一元二次方程ax2+4x﹣2=0有实数根,则a的取值范围为 ___ .
16.如图,矩形 中,
中,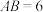 ,
,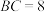 ,对角线
,对角线 的垂直平分线
的垂直平分线 交
交 于点
于点 、交
、交 于点
于点 ,则线段
,则线段 的长为
的长为 __ .

 中,
中,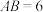 ,
,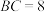 ,对角线
,对角线 的垂直平分线
的垂直平分线 交
交 于点
于点 、交
、交 于点
于点 ,则线段
,则线段 的长为
的长为 
17.若实数 满足
满足 ,则
,则
__ .
 满足
满足 ,则
,则
18.已知,在 中,
中, ,
, ,
, ,则
,则 的面积为
的面积为 __ .
 中,
中, ,
, ,
, ,则
,则 的面积为
的面积为 19.已知非负实数 ,
, ,
, 满足
满足 ,设
,设 的最大值为
的最大值为 ,最小值为
,最小值为 ,则
,则 的值为
的值为 __ .
 ,
, ,
, 满足
满足 ,设
,设 的最大值为
的最大值为 ,最小值为
,最小值为 ,则
,则 的值为
的值为 20.如图,矩形 ,
, ,
, ,点
,点 在
在 轴正半轴上,点
轴正半轴上,点 在
在 轴正半轴上.当点
轴正半轴上.当点 在
在 轴上运动时,点
轴上运动时,点 也随之在
也随之在 轴上运动,在这个运动过程中,点
轴上运动,在这个运动过程中,点 到原点
到原点 的最大距离为
的最大距离为 __ .

 ,
, ,
, ,点
,点 在
在 轴正半轴上,点
轴正半轴上,点 在
在 轴正半轴上.当点
轴正半轴上.当点 在
在 轴上运动时,点
轴上运动时,点 也随之在
也随之在 轴上运动,在这个运动过程中,点
轴上运动,在这个运动过程中,点 到原点
到原点 的最大距离为
的最大距离为 
21.计算: .
.
 .
.22.如图,点 、
、 、
、 、
、 在同一条直线上,
在同一条直线上, ,
, ,
, .
.
求证:(1) ;
;
(2)四边形 是平行四边形.
是平行四边形.

 、
、 、
、 、
、 在同一条直线上,
在同一条直线上, ,
, ,
, .
.求证:(1)
 ;
;(2)四边形
 是平行四边形.
是平行四边形.
23.某学校为了解全校学生对电视节目(新闻、体育、动画、娱乐、戏曲)的喜爱情况,从全校学生中随机抽取部分学生进行问卷调查,并把调查结果绘制成两幅不完整的统计图.

请根据以上信息,解答下列问题
(1)这次被调查的学生共有多少名?
(2)请将条形统计图补充完整;
(3)若该校有3000名学生,估计全校学生中喜欢体育节目的约有多少名?
(4)该校宣传部需要宣传干事,现决定从喜欢新闻节目的甲、乙、丙、丁四名同学中选取2名,用树状图或列表法求恰好选中甲、乙两位同学的概率.

请根据以上信息,解答下列问题
(1)这次被调查的学生共有多少名?
(2)请将条形统计图补充完整;
(3)若该校有3000名学生,估计全校学生中喜欢体育节目的约有多少名?
(4)该校宣传部需要宣传干事,现决定从喜欢新闻节目的甲、乙、丙、丁四名同学中选取2名,用树状图或列表法求恰好选中甲、乙两位同学的概率.
24.在一次课外活动中,某数学兴趣小组测量一棵树 的高度.如图所示,测得斜坡
的高度.如图所示,测得斜坡 的坡度
的坡度 ,坡底
,坡底 的长为8米,在
的长为8米,在 处测得树
处测得树 顶部
顶部 的仰角为
的仰角为 ,在
,在 处测得树
处测得树 顶部
顶部 的仰角为
的仰角为 ,求树高
,求树高 .(结果保留根号)
.(结果保留根号)

 的高度.如图所示,测得斜坡
的高度.如图所示,测得斜坡 的坡度
的坡度 ,坡底
,坡底 的长为8米,在
的长为8米,在 处测得树
处测得树 顶部
顶部 的仰角为
的仰角为 ,在
,在 处测得树
处测得树 顶部
顶部 的仰角为
的仰角为 ,求树高
,求树高 .(结果保留根号)
.(结果保留根号)
25.如图,一次函数 的图象与反比例函数
的图象与反比例函数 的图像相交于
的图像相交于 、
、 两点.
两点.
(1)求一次函数和反比例函数的解析式;
(2)根据图象,直接写出满足 的
的 的取值范围;
的取值范围;
(3)若点 在线段
在线段 上,且
上,且 ,求点
,求点 的坐标.
的坐标.

 的图象与反比例函数
的图象与反比例函数 的图像相交于
的图像相交于 、
、 两点.
两点.(1)求一次函数和反比例函数的解析式;
(2)根据图象,直接写出满足
 的
的 的取值范围;
的取值范围;(3)若点
 在线段
在线段 上,且
上,且 ,求点
,求点 的坐标.
的坐标.
26.为迎接“五一”小长假购物高潮,某品牌专卖店准备购进甲、乙两种衬衫,其中甲、乙两种衬衫的进价和售价如下表:
若用3000元购进甲种衬衫的数量与用2700元购进乙种衬衫的数量相同.
(1)求甲、乙两种衬衫每件的进价;
(2)要使购进的甲、乙两种衬衫共300件的总利润不少于34000元,且不超过34700元,问该专卖店有几种进货方案;
(3)在(2)的条件下,专卖店准备对甲种衬衫进行优惠促销活动,决定对甲种衬衫每件优惠 元
元 出售,乙种衬衫售价不变,那么该专卖店要获得最大利润应如何进货?
出售,乙种衬衫售价不变,那么该专卖店要获得最大利润应如何进货?
| 衬衫价格 | 甲 | 乙 |
进价(元 件) 件) |  |  |
售价(元 件) 件) | 260 | 180 |
(1)求甲、乙两种衬衫每件的进价;
(2)要使购进的甲、乙两种衬衫共300件的总利润不少于34000元,且不超过34700元,问该专卖店有几种进货方案;
(3)在(2)的条件下,专卖店准备对甲种衬衫进行优惠促销活动,决定对甲种衬衫每件优惠
 元
元 出售,乙种衬衫售价不变,那么该专卖店要获得最大利润应如何进货?
出售,乙种衬衫售价不变,那么该专卖店要获得最大利润应如何进货?27.如图, 是
是 的直径,
的直径, 、
、 是
是 上两点,且
上两点,且 ,过点
,过点 的直线
的直线 交
交 的延长线于点
的延长线于点 ,交
,交 的延长线于点
的延长线于点 ,连接
,连接 、
、 交于点
交于点 .
.
(1)求证: 是
是 的切线;
的切线;
(2)若 ,
, 的半径为2,求阴影部分的面积;
的半径为2,求阴影部分的面积;
(3)连结 ,在(2)的条件下,求
,在(2)的条件下,求 的长.
的长.

 是
是 的直径,
的直径, 、
、 是
是 上两点,且
上两点,且 ,过点
,过点 的直线
的直线 交
交 的延长线于点
的延长线于点 ,交
,交 的延长线于点
的延长线于点 ,连接
,连接 、
、 交于点
交于点 .
.(1)求证:
 是
是 的切线;
的切线;(2)若
 ,
, 的半径为2,求阴影部分的面积;
的半径为2,求阴影部分的面积;(3)连结
 ,在(2)的条件下,求
,在(2)的条件下,求 的长.
的长.
28.如图,抛物线 与
与 轴交于
轴交于 、
、 两点,与
两点,与 轴交于点
轴交于点 .直线
.直线 与抛物线交于
与抛物线交于 、
、 两点,与
两点,与 轴交于点
轴交于点 ,点
,点 的坐标为
的坐标为 .
.
(1)求抛物线的解析式与直线 的解析式;
的解析式;
(2)若点 是抛物线上的点且在直线
是抛物线上的点且在直线 上方,连接
上方,连接 、
、 ,求当
,求当 面积最大时点
面积最大时点 的坐标及该面积的最大值;
的坐标及该面积的最大值;
(3)若点 是
是 轴上的点,且
轴上的点,且 ,求点
,求点 的坐标.
的坐标.

 与
与 轴交于
轴交于 、
、 两点,与
两点,与 轴交于点
轴交于点 .直线
.直线 与抛物线交于
与抛物线交于 、
、 两点,与
两点,与 轴交于点
轴交于点 ,点
,点 的坐标为
的坐标为 .
.(1)求抛物线的解析式与直线
 的解析式;
的解析式;(2)若点
 是抛物线上的点且在直线
是抛物线上的点且在直线 上方,连接
上方,连接 、
、 ,求当
,求当 面积最大时点
面积最大时点 的坐标及该面积的最大值;
的坐标及该面积的最大值;(3)若点
 是
是 轴上的点,且
轴上的点,且 ,求点
,求点 的坐标.
的坐标.
 搜索
搜索
 难度系数:0.85
难度系数:0.85  答案解析
答案解析
 有奖纠错
有奖纠错
