全一卷
1.已知 ,
, 为整数,且满足
为整数,且满足 ,则
,则 的可能的值有( )
的可能的值有( )
 ,
, 为整数,且满足
为整数,且满足 ,则
,则 的可能的值有( )
的可能的值有( )| A.1个 | B.2个 | C.3个 | D.4个 |
2.已知非负实数 ,
, ,
, 满足
满足 ,则
,则 的最大值为( )
的最大值为( )
 ,
, ,
, 满足
满足 ,则
,则 的最大值为( )
的最大值为( )A.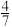 | B. | C. | D. |
3.在△ABC中,AB=AC,D为BC的中点,BE⊥AC于E,交AD于P,已知BP=3,PE=1,则AE=( )
A. | B. | C. | D.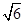 |
4.6张不同的卡片上分别写有数字2,2,4,4,6,6,从中取出3张,则这3张卡片上所写的数字可以作为三角形的三边长的概率是( )
A. | B. | C. | D. |
5.设 表示不超过实数
表示不超过实数 的最大整数,令
的最大整数,令 .已知实数
.已知实数 满足
满足 ,则
,则 ( )
( )
 表示不超过实数
表示不超过实数 的最大整数,令
的最大整数,令 .已知实数
.已知实数 满足
满足 ,则
,则 ( )
( )A. | B. | C. | D.1 |
6.在 中,
中, ,D在
,D在 上,E在
上,E在 上,使得
上,使得 为等腰直角三角形,
为等腰直角三角形, ,则
,则 的长为( )
的长为( )
 中,
中, ,D在
,D在 上,E在
上,E在 上,使得
上,使得 为等腰直角三角形,
为等腰直角三角形, ,则
,则 的长为( )
的长为( )A. | B. | C. | D. |
7.已知实数 ,
, ,
, 满足
满足 ,
, ,则
,则
__________ .
 ,
, ,
, 满足
满足 ,
, ,则
,则
8.使得不等式 对唯一的整数
对唯一的整数 成立的最大正整数
成立的最大正整数 为
为_____ .
 对唯一的整数
对唯一的整数 成立的最大正整数
成立的最大正整数 为
为9.已知 为等腰
为等腰 内一点,
内一点, ,
, ,
, 为
为 的中点,
的中点, 与
与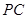 交于点
交于点 ,如果点
,如果点 为
为 的内心(三角形的三条内角平分线的交点),则
的内心(三角形的三条内角平分线的交点),则
_____ .

 为等腰
为等腰 内一点,
内一点, ,
, ,
, 为
为 的中点,
的中点, 与
与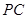 交于点
交于点 ,如果点
,如果点 为
为 的内心(三角形的三条内角平分线的交点),则
的内心(三角形的三条内角平分线的交点),则

10.已知正整数 ,
, ,
, 满足:
满足: ,
, ,
, ,则
,则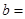
__________ .
 ,
, ,
, 满足:
满足: ,
, ,
, ,则
,则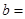
11.设实数 ,
, 满足
满足 ,
, ,求
,求 的值.
的值.
 ,
, 满足
满足 ,
, ,求
,求 的值.
的值.12.如图,在平行四边形 中,
中, 为对角线
为对角线 上一点,且满足
上一点,且满足 ,
, 的延长线与
的延长线与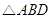 的外接圆交于点
的外接圆交于点 .
.
证明: .
.

 中,
中, 为对角线
为对角线 上一点,且满足
上一点,且满足 ,
, 的延长线与
的延长线与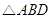 的外接圆交于点
的外接圆交于点 .
.证明:
 .
.
13.设 是整数,如果存在整数
是整数,如果存在整数 ,
, ,
,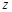 满足
满足 ,则称
,则称 具有性质
具有性质 .在1,5,2013,2014这四个数中,哪些数具有性质
.在1,5,2013,2014这四个数中,哪些数具有性质 ,哪些数不具有性质
,哪些数不具有性质 ?并说明理由.
?并说明理由.
 是整数,如果存在整数
是整数,如果存在整数 ,
, ,
,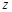 满足
满足 ,则称
,则称 具有性质
具有性质 .在1,5,2013,2014这四个数中,哪些数具有性质
.在1,5,2013,2014这四个数中,哪些数具有性质 ,哪些数不具有性质
,哪些数不具有性质 ?并说明理由.
?并说明理由. 搜索
搜索
 难度系数:0.65
难度系数:0.65  答案解析
答案解析
 有奖纠错
有奖纠错
