全一卷
1.计算: ( )
( )
 ( )
( )| A.1 | B.-1 | C.6 | D.-6 |
2.下列图形中,是轴对称图形的是( )
A. | B. | C. | D. |
3.计算: ( )
( )
 ( )
( )A. | B. | C. | D. |
4.如图,点D、E分别在线段 、
、 上,连接
上,连接 、
、 .若
.若 ,
, ,
, ,则
,则 的大小为( )
的大小为( )

 、
、 上,连接
上,连接 、
、 .若
.若 ,
, ,
, ,则
,则 的大小为( )
的大小为( )
| A.60° | B.70° | C.75° | D.85° |
5.如图,在菱形 中,
中, ,连接
,连接 、
、 ,则
,则 的值为( )
的值为( )

 中,
中, ,连接
,连接 、
、 ,则
,则 的值为( )
的值为( )
A. | B. | C. | D. |
6.在平面直角坐标系中,若将一次函数 的图象向左平移3个单位后,得到一个正比例函数的图象,则m的值为( )
的图象向左平移3个单位后,得到一个正比例函数的图象,则m的值为( )
 的图象向左平移3个单位后,得到一个正比例函数的图象,则m的值为( )
的图象向左平移3个单位后,得到一个正比例函数的图象,则m的值为( )| A.-5 | B.5 | C.-6 | D.6 |
7.如图, 、
、 、
、 、
、 是四根长度均为5cm的火柴棒,点A、C、E共线.若
是四根长度均为5cm的火柴棒,点A、C、E共线.若 ,
, ,则线段
,则线段 的长度为( )
的长度为( )

 、
、 、
、 、
、 是四根长度均为5cm的火柴棒,点A、C、E共线.若
是四根长度均为5cm的火柴棒,点A、C、E共线.若 ,
, ,则线段
,则线段 的长度为( )
的长度为( )
| A.6 cm | B.7 cm | C. | D.8cm |
8.下表中列出的是一个二次函数的自变量x与函数y的几组对应值:
下列各选项中,正确的是
 | … | -2 | 0 | 1 | 3 | … |
 | … | 6 | -4 | -6 | -4 | … |
| A.这个函数的图象开口向下 |
| B.这个函数的图象与x轴无交点 |
| C.这个函数的最小值小于-6 |
D.当 时,y的值随x值的增大而增大 时,y的值随x值的增大而增大 |
9.分解因式:
______ .

10.正九边形一个内角的度数为______ .
11.幻方,最早源于我国,古人称之为纵横图.如图所示的幻方中,各行、各列及各条对角线上的三个数字之和均相等,则图中a的值为______ .
| -1 | -6 | 1 |
| 0 | a | -4 |
| -5 | 2 | -3 |
12.若 ,
, 是反比例函数
是反比例函数 图象上的两点,则
图象上的两点,则 、
、 的大小关系是
的大小关系是
______  (填“>”、“=”或“<”)
(填“>”、“=”或“<”)
 ,
, 是反比例函数
是反比例函数 图象上的两点,则
图象上的两点,则 、
、 的大小关系是
的大小关系是
 (填“>”、“=”或“<”)
(填“>”、“=”或“<”)13.如图,正方形 的边长为4,
的边长为4, 的半径为1.若
的半径为1.若 在正方形
在正方形 内平移(
内平移( 可以与该正方形的边相切),则点A到
可以与该正方形的边相切),则点A到 上的点的距离的最大值为
上的点的距离的最大值为______ .
 的边长为4,
的边长为4, 的半径为1.若
的半径为1.若 在正方形
在正方形 内平移(
内平移( 可以与该正方形的边相切),则点A到
可以与该正方形的边相切),则点A到 上的点的距离的最大值为
上的点的距离的最大值为
14.计算: .
.
 .
.15.解不等式组:

16.解方程: .
.
 .
.17.如图,已知直线 ,直线
,直线 分别与
分别与 、
、 交于点
交于点 、
、 .请用尺规作图法,在线段
.请用尺规作图法,在线段 上求作点
上求作点 ,使点
,使点 到
到 、
、 的距离相等.(保留作图痕迹,不写作法)
的距离相等.(保留作图痕迹,不写作法)

 ,直线
,直线 分别与
分别与 、
、 交于点
交于点 、
、 .请用尺规作图法,在线段
.请用尺规作图法,在线段 上求作点
上求作点 ,使点
,使点 到
到 、
、 的距离相等.(保留作图痕迹,不写作法)
的距离相等.(保留作图痕迹,不写作法)
18.如图, ,
, ,点
,点 在
在 上,且
上,且 .求证:
.求证: .
.
 ,
, ,点
,点 在
在 上,且
上,且 .求证:
.求证: .
.
19.一家商店在销售某种服装(每件的标价相同)时,按这种服装每件标价的8折销售10件的销售额,与按这种服装每件的标价降低30元销售11件的销售额相等.求这种服装每件的标价.
20.从一副普通的扑克牌中取出四张牌,它们的牌面数字分别为2,3,3,6.
(1)将这四张扑克牌背面朝上,洗匀,从中随机抽取一张,则抽取的这张牌的牌面数字是3的概率为 ;
(2)将这四张扑克牌背面朝上,洗匀.从中随机抽取一张,不放回,再从剩余的三张牌中随机抽取一张.请利用画树状图或列表的方法,求抽取的这两张牌的面数字恰好相同的概率.
(1)将这四张扑克牌背面朝上,洗匀,从中随机抽取一张,则抽取的这张牌的牌面数字是3的概率为 ;
(2)将这四张扑克牌背面朝上,洗匀.从中随机抽取一张,不放回,再从剩余的三张牌中随机抽取一张.请利用画树状图或列表的方法,求抽取的这两张牌的面数字恰好相同的概率.
21.一座吊桥的钢索立柱 两侧各有若干条斜拉的钢索,大致如图所示.小明和小亮想用测量知识测较长钢索
两侧各有若干条斜拉的钢索,大致如图所示.小明和小亮想用测量知识测较长钢索 的长度,他们测得
的长度,他们测得 为30°,由于B、D两点间的距离不易测得,通过探究和测量,发现
为30°,由于B、D两点间的距离不易测得,通过探究和测量,发现 恰好为45°,点B与点C之间的距离约为16m.已知点B、C、D共线,
恰好为45°,点B与点C之间的距离约为16m.已知点B、C、D共线, .求钢索
.求钢索 的长度.(结果保留根号)
的长度.(结果保留根号)

 两侧各有若干条斜拉的钢索,大致如图所示.小明和小亮想用测量知识测较长钢索
两侧各有若干条斜拉的钢索,大致如图所示.小明和小亮想用测量知识测较长钢索 的长度,他们测得
的长度,他们测得 为30°,由于B、D两点间的距离不易测得,通过探究和测量,发现
为30°,由于B、D两点间的距离不易测得,通过探究和测量,发现 恰好为45°,点B与点C之间的距离约为16m.已知点B、C、D共线,
恰好为45°,点B与点C之间的距离约为16m.已知点B、C、D共线, .求钢索
.求钢索 的长度.(结果保留根号)
的长度.(结果保留根号)
22.今年9月,第十四届全国运动会将在陕西省举行本届全运会主场馆在西安,开幕式、闭幕式均在西安举行.某校气象兴趣小组的同学们想预估一下西安市今年9月份日平均气温状况.他们收集了西安市近五年9月份每天的日平均气温,从中随机抽取了60天的日平均气温,并绘制成如下统计图:

根据以上信息,回答下列问题:
(1)这60天的日平均气温的中位数为______,众数为______;
(2)求这60天的日平均气温的平均数;
(3)若日平均气温在18℃~21℃的范围内(包含18℃和21℃)为“舒适温度”.请预估西安市今年9月份日平均气温为“舒适温度”的天数.

根据以上信息,回答下列问题:
(1)这60天的日平均气温的中位数为______,众数为______;
(2)求这60天的日平均气温的平均数;
(3)若日平均气温在18℃~21℃的范围内(包含18℃和21℃)为“舒适温度”.请预估西安市今年9月份日平均气温为“舒适温度”的天数.
23.在一次机器“猫”抓机器“鼠”的展演测试中,“鼠”先从起点出发,1min后,“猫”从同一起点出发去追“鼠”,抓住“鼠”并稍作停留后,“猫”抓着“鼠”沿原路返回“鼠”、“猫”距起点的距离 与时间
与时间 之间的关系如图所示.
之间的关系如图所示.
(1)在“猫”追“鼠”的过程中,“猫”的平均速度与“鼠”的平均速度的差是______ ;
;
(2)求 的函数表达式;
的函数表达式;
(3)求“猫”从起点出发到返回至起点所用的时间.

 与时间
与时间 之间的关系如图所示.
之间的关系如图所示.(1)在“猫”追“鼠”的过程中,“猫”的平均速度与“鼠”的平均速度的差是______
 ;
;(2)求
 的函数表达式;
的函数表达式;(3)求“猫”从起点出发到返回至起点所用的时间.

24.如图, 是
是 的直径,点E、F在
的直径,点E、F在 上,且
上,且 ,连接
,连接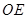 、
、 ,过点
,过点 作
作 的切线,分别与
的切线,分别与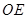 、
、 的延长线交于点C、D.
的延长线交于点C、D.

(1)求证: ;
;
(2)若 ,
, ,求线段
,求线段 的长.
的长.
 是
是 的直径,点E、F在
的直径,点E、F在 上,且
上,且 ,连接
,连接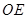 、
、 ,过点
,过点 作
作 的切线,分别与
的切线,分别与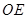 、
、 的延长线交于点C、D.
的延长线交于点C、D.
(1)求证:
 ;
;(2)若
 ,
, ,求线段
,求线段 的长.
的长.25.已知抛物线 与x轴交于点A、B(其中A在点B的左侧),与y轴交于点C.
与x轴交于点A、B(其中A在点B的左侧),与y轴交于点C.
(1)求点B、C的坐标;
(2)设点 与点C关于该抛物线的对称轴对称在y轴上是否存在点P,使
与点C关于该抛物线的对称轴对称在y轴上是否存在点P,使 与
与 相似且
相似且 与
与 是对应边?若存在,求点P的坐标;若不存在,请说明理由.
是对应边?若存在,求点P的坐标;若不存在,请说明理由.
 与x轴交于点A、B(其中A在点B的左侧),与y轴交于点C.
与x轴交于点A、B(其中A在点B的左侧),与y轴交于点C.(1)求点B、C的坐标;
(2)设点
 与点C关于该抛物线的对称轴对称在y轴上是否存在点P,使
与点C关于该抛物线的对称轴对称在y轴上是否存在点P,使 与
与 相似且
相似且 与
与 是对应边?若存在,求点P的坐标;若不存在,请说明理由.
是对应边?若存在,求点P的坐标;若不存在,请说明理由.26.问题提出
(1)如图1,在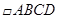 中,
中, ,
, ,
, ,E是
,E是 的中点,点F在
的中点,点F在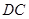 上且
上且 求四边形
求四边形 的面积.(结果保留根号)
的面积.(结果保留根号)
问题解决
(2)某市进行河滩治理,优化美化人居生态环境.如图2所示,现规划在河畔的一处滩地上建一个五边形河畔公园 按设计要求,要在五边形河畔公园
按设计要求,要在五边形河畔公园 内挖一个四边形人工湖
内挖一个四边形人工湖 ,使点O、P、M、N分别在边
,使点O、P、M、N分别在边 、
、 、
、 、
、 上,且满足
上,且满足 ,
, .已知五边形
.已知五边形 中,
中, ,
, ,
, ,
, ,
, .满足人工湖周边各功能场所及绿化用地需要,想让人工湖面积尽可能小.请问,是否存在符合设计要求的面积最小的四边形人工湖
.满足人工湖周边各功能场所及绿化用地需要,想让人工湖面积尽可能小.请问,是否存在符合设计要求的面积最小的四边形人工湖 ?若存在,求四边形
?若存在,求四边形 面积的最小值及这时点
面积的最小值及这时点 到点
到点 的距离;若不存在,请说明理由.
的距离;若不存在,请说明理由.

(1)如图1,在
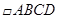 中,
中, ,
, ,
, ,E是
,E是 的中点,点F在
的中点,点F在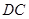 上且
上且 求四边形
求四边形 的面积.(结果保留根号)
的面积.(结果保留根号)问题解决
(2)某市进行河滩治理,优化美化人居生态环境.如图2所示,现规划在河畔的一处滩地上建一个五边形河畔公园
 按设计要求,要在五边形河畔公园
按设计要求,要在五边形河畔公园 内挖一个四边形人工湖
内挖一个四边形人工湖 ,使点O、P、M、N分别在边
,使点O、P、M、N分别在边 、
、 、
、 、
、 上,且满足
上,且满足 ,
, .已知五边形
.已知五边形 中,
中, ,
, ,
, ,
, ,
, .满足人工湖周边各功能场所及绿化用地需要,想让人工湖面积尽可能小.请问,是否存在符合设计要求的面积最小的四边形人工湖
.满足人工湖周边各功能场所及绿化用地需要,想让人工湖面积尽可能小.请问,是否存在符合设计要求的面积最小的四边形人工湖 ?若存在,求四边形
?若存在,求四边形 面积的最小值及这时点
面积的最小值及这时点 到点
到点 的距离;若不存在,请说明理由.
的距离;若不存在,请说明理由.
 搜索
搜索
 难度系数:0.85
难度系数:0.85  答案解析
答案解析
 有奖纠错
有奖纠错
