全一卷
1. ( )
( )
 ( )
( )A. | B.2021 | C. | D. |
2.“奋斗者”号载人潜水器此前在马里亚纳海沟创造了10909米的我国载人深潜纪录,数据10909用科学记数法可表示为( )
A. | B. | C. | D. |
3.因式分解: ( )
( )
 ( )
( )A. | B. |
C. | D. |
4.如图,设点 是直线
是直线 外一点,
外一点, ,垂足为点
,垂足为点 ,点
,点 是直线
是直线 上的一个动点,连接
上的一个动点,连接 ,则( )
,则( )

 是直线
是直线 外一点,
外一点, ,垂足为点
,垂足为点 ,点
,点 是直线
是直线 上的一个动点,连接
上的一个动点,连接 ,则( )
,则( )
A. | B. | C. | D. |
5.下列计算正确的是( )
A. | B. | C. | D. |
6.某景点今年四月接待游客25万人次,五月接待游客60.5万人次,设该景点今年四月到五月接待游客人次的增长率为 (
( ),则( )
),则( )
 (
( ),则( )
),则( )A. | B. |
C. | D. |
7.某轨道列车共有3节车厢,设乘客从任意一节车厢上车的机会均等,某天甲、乙两位乘客同时乘同一列轨道列车,则甲和乙从同一节车厢上车的概率是( )
A. | B. | C. | D. |
8.在“探索函数 的系数
的系数 ,
, ,
, 与图象的关系”活动中,老师给出了直角坐标系中的四个点:
与图象的关系”活动中,老师给出了直角坐标系中的四个点: ,
, ,
, ,
, ,同学们探索了经过这四个点中的三个点的二次函数的图象,发现这些图象对应的函数表达式各不相同,其中
,同学们探索了经过这四个点中的三个点的二次函数的图象,发现这些图象对应的函数表达式各不相同,其中 的值最大为( )
的值最大为( )

 的系数
的系数 ,
, ,
, 与图象的关系”活动中,老师给出了直角坐标系中的四个点:
与图象的关系”活动中,老师给出了直角坐标系中的四个点: ,
, ,
, ,
, ,同学们探索了经过这四个点中的三个点的二次函数的图象,发现这些图象对应的函数表达式各不相同,其中
,同学们探索了经过这四个点中的三个点的二次函数的图象,发现这些图象对应的函数表达式各不相同,其中 的值最大为( )
的值最大为( )
A. | B. | C. | D. |
9.已知线段 ,按如下步骤作图:①作射线
,按如下步骤作图:①作射线 ,使
,使 ;②作
;②作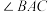 的平分线
的平分线 ;③以点
;③以点 为圆心,
为圆心, 长为半径作弧,交
长为半径作弧,交 于点
于点 ;④过点
;④过点 作
作 于点
于点 ,则
,则 ( )
( )

 ,按如下步骤作图:①作射线
,按如下步骤作图:①作射线 ,使
,使 ;②作
;②作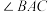 的平分线
的平分线 ;③以点
;③以点 为圆心,
为圆心, 长为半径作弧,交
长为半径作弧,交 于点
于点 ;④过点
;④过点 作
作 于点
于点 ,则
,则 ( )
( )
A. | B. | C. | D. |
10.已知 和
和 均是以
均是以 为自变量的函数,当
为自变量的函数,当 时,函数值分别为
时,函数值分别为 和
和 ,若存在实数
,若存在实数 ,使得
,使得 ,则称函数
,则称函数 和
和 具有性质
具有性质 .以下函数
.以下函数 和
和 具有性质
具有性质 的是( )
的是( )
 和
和 均是以
均是以 为自变量的函数,当
为自变量的函数,当 时,函数值分别为
时,函数值分别为 和
和 ,若存在实数
,若存在实数 ,使得
,使得 ,则称函数
,则称函数 和
和 具有性质
具有性质 .以下函数
.以下函数 和
和 具有性质
具有性质 的是( )
的是( )A. 和 和 |
B. 和 和 |
C. 和 和 |
D. 和 和 |
11.sin30°的值为_____ .
12.计算:2a+3a=_____ .
13.如图,已知 的半径为1,点
的半径为1,点 是
是 外一点,且
外一点,且 .若
.若 是
是 的切线,
的切线, 为切点,连接
为切点,连接 ,则
,则
_____ .

 的半径为1,点
的半径为1,点 是
是 外一点,且
外一点,且 .若
.若 是
是 的切线,
的切线, 为切点,连接
为切点,连接 ,则
,则

14.现有甲、乙两种糖果的单价与千克数如下表所示.
将这2千克甲种糖果和3千克乙种糖果混合成5千克什锦糖果,若商家用加权平均数来确定什锦糖果的单价,则这5千克什锦糖果的单价为______ 元/千克.
甲种糖果 | 乙种糖果 | |
单价(元/千克) | 30 | 20 |
千克数 | 2 | 3 |
将这2千克甲种糖果和3千克乙种糖果混合成5千克什锦糖果,若商家用加权平均数来确定什锦糖果的单价,则这5千克什锦糖果的单价为
15.如图,在直角坐标系中,以点 为端点的四条射线
为端点的四条射线 ,
, ,
, ,
, 分别过点
分别过点 ,点
,点 ,点
,点 ,点
,点 ,则
,则
______  (填“
(填“ ”“
”“ ”“
”“ ”中的一个).
”中的一个).

 为端点的四条射线
为端点的四条射线 ,
, ,
, ,
, 分别过点
分别过点 ,点
,点 ,点
,点 ,点
,点 ,则
,则
 (填“
(填“ ”“
”“ ”“
”“ ”中的一个).
”中的一个).
16.如图是一张矩形纸片 ,点
,点 是对角线
是对角线 的中点,点
的中点,点 在
在 边上,把
边上,把 沿直线
沿直线 折叠,使点
折叠,使点 落在对角线
落在对角线 上的点
上的点 处,连接
处,连接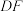 ,
, .若
.若 ,则
,则
_____ 度.

 ,点
,点 是对角线
是对角线 的中点,点
的中点,点 在
在 边上,把
边上,把 沿直线
沿直线 折叠,使点
折叠,使点 落在对角线
落在对角线 上的点
上的点 处,连接
处,连接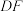 ,
, .若
.若 ,则
,则

17.以下是圆圆解不等式组

的解答过程.
解:由①,得 ,
,
所以 .
.
由②,得 ,
,
所以 ,
,
所以 .
.
所以原不等式组的解是 .
.
圆圆的解答过程是否有错误?如果有错误,写出正确的解答过程.

的解答过程.
解:由①,得
 ,
,所以
 .
.由②,得
 ,
,所以
 ,
,所以
 .
.所以原不等式组的解是
 .
.圆圆的解答过程是否有错误?如果有错误,写出正确的解答过程.
18.为了解某校某年级学生一分钟跳绳情况,对该年级全部360名学生进行一分钟跳绳次数的测试,并把测得数据分成四组,绘制成如图所示的频数表和未完成的频数直方图(每一组不含前一个边界值,含后一个边界值).

某校某年级360名学生一分钟跳绳次数的频数表
(1)求 的值.
的值.
(2)把频数直方图补充完整.
(3)求该年级一分钟跳绳次数在190次以上的学生数占该年级全部学生数的百分比.

某校某年级360名学生一分钟跳绳次数的频数表
组别(次) | 频数 |
100~130 | 48 |
130~160 | 96 |
160~190 | a |
190~220 | 72 |
 的值.
的值.(2)把频数直方图补充完整.
(3)求该年级一分钟跳绳次数在190次以上的学生数占该年级全部学生数的百分比.
19.在① ,②
,② ,③
,③ 这三个条件中选择其中一个,补充在下面的问题中,并完成问题的解答.
这三个条件中选择其中一个,补充在下面的问题中,并完成问题的解答.

问题:如图,在 中,
中, ,点
,点 在
在 边上(不与点
边上(不与点 ,点
,点 重合),点
重合),点 在
在 边上(不与点
边上(不与点 ,点
,点 重合),连接
重合),连接 ,
, ,
, 与
与 相交于点
相交于点 .若______,求证:
.若______,求证: .
.
注:如果选择多个条件分别作答,按第一个解答计分.
 ,②
,② ,③
,③ 这三个条件中选择其中一个,补充在下面的问题中,并完成问题的解答.
这三个条件中选择其中一个,补充在下面的问题中,并完成问题的解答.
问题:如图,在
 中,
中, ,点
,点 在
在 边上(不与点
边上(不与点 ,点
,点 重合),点
重合),点 在
在 边上(不与点
边上(不与点 ,点
,点 重合),连接
重合),连接 ,
, ,
, 与
与 相交于点
相交于点 .若______,求证:
.若______,求证: .
.注:如果选择多个条件分别作答,按第一个解答计分.
20.在直角坐标系中,设函数 (
( 是常数,
是常数, ,
, )与函数
)与函数 (
( 是常数,
是常数, )的图象交于点A,点A关于
)的图象交于点A,点A关于 轴的对称点为点
轴的对称点为点 .
.

(1)若点 的坐标为
的坐标为 ,
,
①求 ,
, 的值.
的值.
②当 时,直接写出
时,直接写出 的取值范围.
的取值范围.
(2)若点 在函数
在函数 (
( 是常数,
是常数, )的图象上,求
)的图象上,求 的值.
的值.
 (
( 是常数,
是常数, ,
, )与函数
)与函数 (
( 是常数,
是常数, )的图象交于点A,点A关于
)的图象交于点A,点A关于 轴的对称点为点
轴的对称点为点 .
.
(1)若点
 的坐标为
的坐标为 ,
,①求
 ,
, 的值.
的值.②当
 时,直接写出
时,直接写出 的取值范围.
的取值范围.(2)若点
 在函数
在函数 (
( 是常数,
是常数, )的图象上,求
)的图象上,求 的值.
的值.21.如图,在 中,
中, 的平分线
的平分线 交
交 边于点
边于点 ,
, 于点
于点 .已知
.已知 ,
, .
.

(1)求证: .
.
(2)若 ,求
,求 的面积
的面积
 中,
中, 的平分线
的平分线 交
交 边于点
边于点 ,
, 于点
于点 .已知
.已知 ,
, .
.
(1)求证:
 .
.(2)若
 ,求
,求 的面积
的面积22.在直角坐标系中,设函数 (
( ,
, 是常数,
是常数,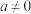 ).
).
(1)若该函数的图象经过 和
和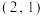 两点,求函数的表达式,并写出函数图象的顶点坐标.
两点,求函数的表达式,并写出函数图象的顶点坐标.
(2)写出一组 ,
, 的值,使函数
的值,使函数 的图象与
的图象与 轴有两个不同的交点,并说明理由.
轴有两个不同的交点,并说明理由.
(3)已知 ,当
,当 (
(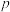 ,
, 是实数,
是实数, )时,该函数对应的函数值分别为
)时,该函数对应的函数值分别为 ,
, .若
.若 ,求证
,求证 .
.
 (
( ,
, 是常数,
是常数,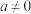 ).
).(1)若该函数的图象经过
 和
和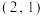 两点,求函数的表达式,并写出函数图象的顶点坐标.
两点,求函数的表达式,并写出函数图象的顶点坐标.(2)写出一组
 ,
, 的值,使函数
的值,使函数 的图象与
的图象与 轴有两个不同的交点,并说明理由.
轴有两个不同的交点,并说明理由.(3)已知
 ,当
,当 (
(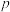 ,
, 是实数,
是实数, )时,该函数对应的函数值分别为
)时,该函数对应的函数值分别为 ,
, .若
.若 ,求证
,求证 .
.23.如图,锐角三角形 内接于
内接于 ,
,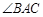 的平分线
的平分线 交
交 于点
于点 ,交
,交 边于点
边于点 ,连接
,连接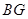 .
.

(1)求证:
 .
.
(2)已知 ,
, ,求线段
,求线段 的长(用含
的长(用含 ,
, 的代数式表示).
的代数式表示).
(3)已知点 在线段
在线段 上(不与点
上(不与点 ,点
,点 重合),点
重合),点 在线段
在线段 上(不与点
上(不与点 ,点
,点 重合),
重合), ,求证:
,求证: .
.
 内接于
内接于 ,
,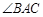 的平分线
的平分线 交
交 于点
于点 ,交
,交 边于点
边于点 ,连接
,连接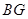 .
.
(1)求证:

 .
.(2)已知
 ,
, ,求线段
,求线段 的长(用含
的长(用含 ,
, 的代数式表示).
的代数式表示).(3)已知点
 在线段
在线段 上(不与点
上(不与点 ,点
,点 重合),点
重合),点 在线段
在线段 上(不与点
上(不与点 ,点
,点 重合),
重合), ,求证:
,求证: .
. 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
