全一卷
1.-2021的绝对值等于( )
| A.2021 | B.-2021 | C. | D. |
2.我国是世界上免费为国民接种新冠疫苗最多的国家,截至2021年6月5日,免费接种数量已超过700000000剂次,将700000000用科学记数法表示为( )
A. | B. | C. | D. |
3.如图所示的几何体,其俯视图是( )


A. | B. |
C. | D. |
4.下列运算正确的是( )
A. | B. |
C. | D. |
5.某校有4000名学生,随机抽取了400名学生进行体重调查,下列说法错误的是( )
| A.总体是该校4000名学生的体重 | B.个体是每一个学生 |
| C.样本是抽取的400名学生的体重 | D.样本容量是400 |
6.如图,正方形 内的图形来自中国古代的太极图,正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称,设正方形
内的图形来自中国古代的太极图,正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称,设正方形 的面积为
的面积为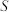 ,黑色部分面积为
,黑色部分面积为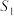 ,则
,则 的比值为( )
的比值为( )

 内的图形来自中国古代的太极图,正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称,设正方形
内的图形来自中国古代的太极图,正方形内切圆中的黑色部分和白色部分关于正方形的中心成中心对称,设正方形 的面积为
的面积为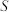 ,黑色部分面积为
,黑色部分面积为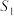 ,则
,则 的比值为( )
的比值为( )
A. | B. | C.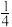 | D. |
7.对于实数 定义运算“☆”如下:
定义运算“☆”如下: ,例如
,例如 ,则方程
,则方程 的根的情况为( )
的根的情况为( )
 定义运算“☆”如下:
定义运算“☆”如下: ,例如
,例如 ,则方程
,则方程 的根的情况为( )
的根的情况为( )| A.没有实数根 | B.只有一个实数根 | C.有两个相等的实数根 | D.有两个不相等的实数根 |
8.若二次函数 的图象如图所示,则一次函数
的图象如图所示,则一次函数 与反比例函数
与反比例函数 在同一个坐标系内的大致图象为( )
在同一个坐标系内的大致图象为( )

 的图象如图所示,则一次函数
的图象如图所示,则一次函数 与反比例函数
与反比例函数 在同一个坐标系内的大致图象为( )
在同一个坐标系内的大致图象为( )
A. | B. |
C. | D. |
9.已知方程 ,则
,则
______ .
 ,则
,则
10.如图是张家界市某周每天最高气温的折线统计图,则这7天的最高气温的中位数是______  .
.

 .
.
11.如图,已知 ,
, 是
是 的平分线,若
的平分线,若 ,则
,则
________ .

 ,
, 是
是 的平分线,若
的平分线,若 ,则
,则

12.不等式 的正整数解为
的正整数解为______ .
 的正整数解为
的正整数解为13.如图, 内接于
内接于 ,
, ,点
,点 是
是 的中点,连接
的中点,连接 ,
, ,
, ,则
,则
_________ .

 内接于
内接于 ,
, ,点
,点 是
是 的中点,连接
的中点,连接 ,
, ,
, ,则
,则

14.如图,在正方形 外取一点
外取一点 ,连接
,连接 ,
, ,
, ,过点
,过点 作
作 的垂线交
的垂线交 于点
于点 ,若
,若 ,
, .下列结论:①
.下列结论:① ;②
;② ;③点
;③点 到直线
到直线 的距离为
的距离为 ;④
;④ ,其中正确结论的序号为
,其中正确结论的序号为______ .

 外取一点
外取一点 ,连接
,连接 ,
, ,
, ,过点
,过点 作
作 的垂线交
的垂线交 于点
于点 ,若
,若 ,
, .下列结论:①
.下列结论:① ;②
;② ;③点
;③点 到直线
到直线 的距离为
的距离为 ;④
;④ ,其中正确结论的序号为
,其中正确结论的序号为
15.计算:

16.先化简 ,然后从0,1,2,3中选一个合适的
,然后从0,1,2,3中选一个合适的 值代入求解.
值代入求解.
 ,然后从0,1,2,3中选一个合适的
,然后从0,1,2,3中选一个合适的 值代入求解.
值代入求解.17.2021年是中国共产党建党100周年,全国各地积极开展“弘扬红色文化,重走长征路”主题教育学习活动,我市“红二方面军长征出发地纪念馆”成为重要的活动基地.据了解,今年3月份该基地接待参观人数10万人,5月份接待参观人数增加到12.1万人.
(1)求这两个月参观人数的月平均增长率;
(2)按照这个增长率,预计6月份的参观人数是多少?
(1)求这两个月参观人数的月平均增长率;
(2)按照这个增长率,预计6月份的参观人数是多少?
18.如图,在矩形 中,对角线
中,对角线 与
与 相交于点
相交于点 ,
, ,对角线
,对角线 所在的直线绕点
所在的直线绕点 顺时针旋转角
顺时针旋转角 ,所得的直线
,所得的直线 分别交
分别交 ,
, 于点
于点 .
.

(1)求证: ;
;
(2)当旋转角 为多少度时,四边形
为多少度时,四边形 为菱形?试说明理由.
为菱形?试说明理由.
 中,对角线
中,对角线 与
与 相交于点
相交于点 ,
, ,对角线
,对角线 所在的直线绕点
所在的直线绕点 顺时针旋转角
顺时针旋转角 ,所得的直线
,所得的直线 分别交
分别交 ,
, 于点
于点 .
.
(1)求证:
 ;
;(2)当旋转角
 为多少度时,四边形
为多少度时,四边形 为菱形?试说明理由.
为菱形?试说明理由.19.为了积极响应中共中央文明办关于“文明用餐”的倡议,某校开展了“你的家庭使用公筷了吗?”的调查活动,并随机抽取了部分学生,对他们家庭用餐使用公筷情况进行统计,统计分类为以下四种:A(完全使用)、B(多数时间使用)、C(偶尔使用)、D(完全不使用),将数据进行整理后,绘制了两幅不完整的统计图.

根据以上信息,解答下列问题:
(1)本次抽取的学生总人数共有_________.
(2)补全条形统计图;
(3)扇形统计图中A对应的扇形的圆心角度数是__________.
(4)为了了解少数学生完全不使用公筷的原因,学校决定从D组的学生中随机抽取两位进行回访,若D组中有3名男生,其余均为女生,请用列表法或画树状图的方法,求抽取的两位学生恰好是一男一女的概率.

根据以上信息,解答下列问题:
(1)本次抽取的学生总人数共有_________.
(2)补全条形统计图;
(3)扇形统计图中A对应的扇形的圆心角度数是__________.
(4)为了了解少数学生完全不使用公筷的原因,学校决定从D组的学生中随机抽取两位进行回访,若D组中有3名男生,其余均为女生,请用列表法或画树状图的方法,求抽取的两位学生恰好是一男一女的概率.
20.如图,在 中,
中, ,
, ,以点
,以点 为圆心,
为圆心, 为半径的圆交
为半径的圆交 的延长线于点
的延长线于点 ,过点
,过点 作
作 的平行线,交
的平行线,交 于点
于点 ,连接
,连接 .
.

(1)求证: 为
为 的切线;
的切线;
(2)若 ,求弧
,求弧 的长.
的长.
 中,
中, ,
, ,以点
,以点 为圆心,
为圆心, 为半径的圆交
为半径的圆交 的延长线于点
的延长线于点 ,过点
,过点 作
作 的平行线,交
的平行线,交 于点
于点 ,连接
,连接 .
.
(1)求证:
 为
为 的切线;
的切线;(2)若
 ,求弧
,求弧 的长.
的长.21.张家界大峡谷玻璃桥是我市又一闻名中外的五星景点.某校初三年级在一次研学活动中,数学研学小组设计以下方案测量桥的高度.如图,在桥面正下方的谷底选一观测点 ,观测到桥面
,观测到桥面 ,
, 的仰角分别为
的仰角分别为 ,测得
,测得 长为320米,求观测点
长为320米,求观测点 到桥面
到桥面 的距离.(结果保留整数,参考数据:
的距离.(结果保留整数,参考数据: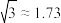 )
)


 ,观测到桥面
,观测到桥面 ,
, 的仰角分别为
的仰角分别为 ,测得
,测得 长为320米,求观测点
长为320米,求观测点 到桥面
到桥面 的距离.(结果保留整数,参考数据:
的距离.(结果保留整数,参考数据: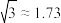 )
)

22.阅读下面的材料:
如果函数 满足:对于自变量
满足:对于自变量 取值范围内的任意
取值范围内的任意 ,
, ,
,
(1)若 ,都有
,都有 ,则称
,则称 是增函数;
是增函数;
(2)若 ,都有
,都有 ,则称
,则称 是减函数.
是减函数.
例题:证明函数 是增函数.
是增函数.
证明:任取 ,且
,且 ,
,
则
∵ 且
且 ,
,
∴ ,
,
∴ ,即
,即 ,
,
∴函数 是增函数.
是增函数.
根据以上材料解答下列问题:
(1)函数 ,
, ,
, ,
, _______,
_______, _______;
_______;
(2)猜想 是函数_________(填“增”或“减”),并证明你的猜想.
是函数_________(填“增”或“减”),并证明你的猜想.
如果函数
 满足:对于自变量
满足:对于自变量 取值范围内的任意
取值范围内的任意 ,
, ,
,(1)若
 ,都有
,都有 ,则称
,则称 是增函数;
是增函数;(2)若
 ,都有
,都有 ,则称
,则称 是减函数.
是减函数.例题:证明函数
 是增函数.
是增函数.证明:任取
 ,且
,且 ,
,
则

∵
 且
且 ,
,
∴
 ,
,
∴
 ,即
,即 ,
,
∴函数
 是增函数.
是增函数.根据以上材料解答下列问题:
(1)函数
 ,
, ,
, ,
, _______,
_______, _______;
_______;(2)猜想
 是函数_________(填“增”或“减”),并证明你的猜想.
是函数_________(填“增”或“减”),并证明你的猜想.23.如图,已知二次函数 的图象经过点
的图象经过点 且与
且与 轴交于原点及点
轴交于原点及点 .
.

(1)求二次函数的表达式;
(2)求顶点 的坐标及直线
的坐标及直线 的表达式;
的表达式;
(3)判断 的形状,试说明理由;
的形状,试说明理由;
(4)若点 为
为 上的动点,且
上的动点,且 的半径为
的半径为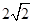 ,一动点
,一动点 从点
从点 出发,以每秒2个单位长度的速度沿线段
出发,以每秒2个单位长度的速度沿线段 匀速运动到点
匀速运动到点 ,再以每秒1个单位长度的速度沿线段
,再以每秒1个单位长度的速度沿线段 匀速运动到点
匀速运动到点 后停止运动,求点
后停止运动,求点 的运动时间
的运动时间 的最小值.
的最小值.
 的图象经过点
的图象经过点 且与
且与 轴交于原点及点
轴交于原点及点 .
.
(1)求二次函数的表达式;
(2)求顶点
 的坐标及直线
的坐标及直线 的表达式;
的表达式;(3)判断
 的形状,试说明理由;
的形状,试说明理由;(4)若点
 为
为 上的动点,且
上的动点,且 的半径为
的半径为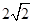 ,一动点
,一动点 从点
从点 出发,以每秒2个单位长度的速度沿线段
出发,以每秒2个单位长度的速度沿线段 匀速运动到点
匀速运动到点 ,再以每秒1个单位长度的速度沿线段
,再以每秒1个单位长度的速度沿线段 匀速运动到点
匀速运动到点 后停止运动,求点
后停止运动,求点 的运动时间
的运动时间 的最小值.
的最小值. 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
