全一卷
1. 的相反数是( )
的相反数是( )
 的相反数是( )
的相反数是( )A. | B.0 | C.3 | D. |
2.下列四个图形中,是中心对称图形的是( )
A. | B. | C. | D. |
3.2021年我国首次发射探测器对火星进行探测.北京时间2月10日晚,“天问一号”探测器在距离地球约192000000km处成功实施制动捕获,随后进入火星轨道.用科学记数法将192000000表示为 的形式,则
的形式,则 的值是( )
的值是( )

 的形式,则
的形式,则 的值是( )
的值是( )
| A.0.192 | B.1.92 | C.19.2 | D.192 |
4.如图,若数轴上两点 ,
, 所对应的实数分别为
所对应的实数分别为 ,
, ,则
,则 的值可能是( )
的值可能是( )

 ,
, 所对应的实数分别为
所对应的实数分别为 ,
, ,则
,则 的值可能是( )
的值可能是( )
| A.2 | B.1 | C. | D.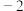 |
5.如图,在 中,
中, ,
, .将
.将 绕点
绕点 逆时针方向旋转
逆时针方向旋转 ,得到
,得到 ,连接
,连接 .则线段
.则线段 的长为( )
的长为( )

 中,
中, ,
, .将
.将 绕点
绕点 逆时针方向旋转
逆时针方向旋转 ,得到
,得到 ,连接
,连接 .则线段
.则线段 的长为( )
的长为( )
| A.1 | B. | C. | D. |
6.其社区针对5月30日前该社区居民接种新冠疫苗的情况开展了问卷调查,共收回6000份有效问卷.经统计,制成如下数据表格.
小杰同学选择扇形统计图分析接种不同针数的居民人数所占总人数的百分比.下面是制作扇形统计图的步骤(顺序打乱):
①计算各部分扇形的圆心角分别为 ,
, ,
, ,
, .
.
②计算出接种不同针数的居民人数占总人数的百分比分别为35%,38%,22%,5%.
③在同一个圆中,根据所得的圆心角度数画出各个扇形,并注明各部分的名称及相应的百分比.
制作扇形统计图的步骤排序正确的是( )

| 接种疫苗针数 | 0 | 1 | 2 | 3 |
| 人数 | 2100 | 2280 | 1320 | 300 |
小杰同学选择扇形统计图分析接种不同针数的居民人数所占总人数的百分比.下面是制作扇形统计图的步骤(顺序打乱):
①计算各部分扇形的圆心角分别为
 ,
, ,
, ,
, .
.②计算出接种不同针数的居民人数占总人数的百分比分别为35%,38%,22%,5%.
③在同一个圆中,根据所得的圆心角度数画出各个扇形,并注明各部分的名称及相应的百分比.
制作扇形统计图的步骤排序正确的是( )

| A.②①③ | B.①③② | C.①②③ | D.③①② |
7.不等式组 的整数解的和为( )
的整数解的和为( )
 的整数解的和为( )
的整数解的和为( )| A.1 | B.0 | C.-1 | D.-2 |
8.某天早晨7:00,小明从家骑自行车去上学,途中因自行车发生故障,就地修车耽误了一段时间,修好车后继续骑行,7:30赶到了学校.图所示的函数图象反映了他骑车上学的整个过程.结合图象,判断下列结论正确的是( )


| A.小明修车花了15min |
| B.小明家距离学校1100m |
| C.小明修好车后花了30min到达学校 |
| D.小明修好车后骑行到学校的平均速度是3m/s |
9.如图,点 ,
, ,
, 是
是 上的三点.若
上的三点.若 ,
, ,则
,则 的大小为( )
的大小为( )

 ,
, ,
, 是
是 上的三点.若
上的三点.若 ,
, ,则
,则 的大小为( )
的大小为( )
A. | B. | C. | D. |
10.在平面直角坐标系中,若直线 不经过第一象限,则关于
不经过第一象限,则关于 的方程
的方程 的实数根的个数为( )
的实数根的个数为( )
 不经过第一象限,则关于
不经过第一象限,则关于 的方程
的方程 的实数根的个数为( )
的实数根的个数为( )| A.0个 | B.1个 | C.2个 | D.1或2个 |
11.16的算术平方根是___________ .
12.因式分解:
______ .

13.如图,点D、E、F分别是△ABC各边的中点,连接DE、EF、DF,若△ABC的周长为10,则△DEF的周长为_______________ .


14.已知点 ,
, 为反比例函数
为反比例函数 图象上的两点,则
图象上的两点,则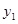 与
与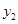 的大小关系是
的大小关系是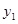
______ 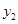 .(填“>”“=”或“<”)
.(填“>”“=”或“<”)
 ,
, 为反比例函数
为反比例函数 图象上的两点,则
图象上的两点,则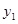 与
与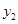 的大小关系是
的大小关系是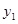
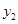 .(填“>”“=”或“<”)
.(填“>”“=”或“<”)15.如图,已知线段 长为4.现按照以下步骤作图:①分别以点
长为4.现按照以下步骤作图:①分别以点 ,
, 为圆心,大于
为圆心,大于 长为半径画弧,两弧分别相交于点
长为半径画弧,两弧分别相交于点 ,
, ;②过
;②过 ,
, 两点作直线,与线段
两点作直线,与线段 相交于点
相交于点 .则
.则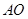 的长为
的长为______ .

 长为4.现按照以下步骤作图:①分别以点
长为4.现按照以下步骤作图:①分别以点 ,
, 为圆心,大于
为圆心,大于 长为半径画弧,两弧分别相交于点
长为半径画弧,两弧分别相交于点 ,
, ;②过
;②过 ,
, 两点作直线,与线段
两点作直线,与线段 相交于点
相交于点 .则
.则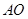 的长为
的长为
16.一只昆虫在如图所示的树枝上寻觅食物,假定昆虫在每个岔路口都会随机选择一条路径,则它获取食物的概率是___ .


17.《九章算术》中有一道阐述“盈不足术”的问题,原文如下:今有共买物,人出八,盈三;人出七,不足四.问人数、物价各几何?意思是:几个人一起去购买某物品,如果每人出8钱,则多了3钱;如果每人出7钱,则少了4钱.问有多少人,物品的价值是多少?该问题中物品的价值是______ 钱.
18.如图,在矩形 中,
中, ,垂足为点
,垂足为点 .若
.若 ,
, ,则
,则 的长为
的长为______ .

 中,
中, ,垂足为点
,垂足为点 .若
.若 ,
, ,则
,则 的长为
的长为
19.计算: .
.
 .
.20.先化简,再从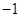 ,0,1,2,
,0,1,2, 中选择一个合适的
中选择一个合适的 的值代入求值.
的值代入求值.
 .
.
 ,0,1,2,
,0,1,2, 中选择一个合适的
中选择一个合适的 的值代入求值.
的值代入求值. .
.21.如图,在正方形 中,对角线
中,对角线 ,
, 相交于点
相交于点 ,点
,点 ,
, 是对角线
是对角线 上的两点,且
上的两点,且 .连接
.连接 ,
,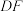 ,
, ,
,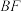 .
.
(1)证明: .
.
(2)若 ,
, ,求四边形
,求四边形 的周长.
的周长.

 中,对角线
中,对角线 ,
, 相交于点
相交于点 ,点
,点 ,
, 是对角线
是对角线 上的两点,且
上的两点,且 .连接
.连接 ,
,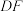 ,
, ,
,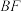 .
.(1)证明:
 .
.(2)若
 ,
, ,求四边形
,求四边形 的周长.
的周长.
22.为庆祝中国共产党成立100周年,某校计划举行“学党史·感党恩”知识竞答活动,并计划购置篮球、钢笔、笔记本作为奖品.采购员刘老师在某文体用品购买了做为奖品的三种物品,回到学校后发现发票被弄花了,有几个数据变得不清楚,如图.

请根据图所示的发票中的信息,帮助刘老师复原弄花的数据,即分别求出购置钢笔、笔记本的数量及对应的金额.

请根据图所示的发票中的信息,帮助刘老师复原弄花的数据,即分别求出购置钢笔、笔记本的数量及对应的金额.
23.为落实湖南省共青团“青年大学习”的号召,某校团委针对该校学生每周参加“青年大学习”的时间(单位:h)进行了随机抽样调查,并将获得的数据绘制成如下统计表和如图所示的统计图,请根据图表中的信息回答下列问题.

(1)求统计表中 ,
, 的值.
的值.
(2)甲同学说“我的周学习时间是此次抽样调查所得数据的中位数”.求甲同学的周学习时间在哪个范围内.
(3)已知该校学生约有20000人,试估计该校学生每周参加“青年大学习”的时间不少于3h的人数.
| 周学习时间 | 频数 | 频率 |
 | 5 | 0.05 |
 | 20 | 0.20 |
 |  | 0.35 |
 | 25 |  |
 | 15 | 0.15 |

(1)求统计表中
 ,
, 的值.
的值.(2)甲同学说“我的周学习时间是此次抽样调查所得数据的中位数”.求甲同学的周学习时间在哪个范围内.
(3)已知该校学生约有20000人,试估计该校学生每周参加“青年大学习”的时间不少于3h的人数.
24.某种冰激凌的外包装可以视为圆锥,它的底面圆直径 与母线
与母线 长之比为
长之比为 .制作这种外包装需要用如图所示的等腰三角形材料,其中
.制作这种外包装需要用如图所示的等腰三角形材料,其中 ,
, .将扇形
.将扇形 围成圆锥时,
围成圆锥时, ,
, 恰好重合.
恰好重合.
(1)求这种加工材料的顶角 的大小
的大小
(2)若圆锥底面圆的直径 为5cm,求加工材料剩余部分(图中阴影部分)的面积.(结果保留
为5cm,求加工材料剩余部分(图中阴影部分)的面积.(结果保留 )
)

 与母线
与母线 长之比为
长之比为 .制作这种外包装需要用如图所示的等腰三角形材料,其中
.制作这种外包装需要用如图所示的等腰三角形材料,其中 ,
, .将扇形
.将扇形 围成圆锥时,
围成圆锥时, ,
, 恰好重合.
恰好重合.(1)求这种加工材料的顶角
 的大小
的大小(2)若圆锥底面圆的直径
 为5cm,求加工材料剩余部分(图中阴影部分)的面积.(结果保留
为5cm,求加工材料剩余部分(图中阴影部分)的面积.(结果保留 )
)
25.如图,在平面直角坐标系中,抛物线 :
: 经过点
经过点 和
和 .
.
(1)求抛物线 的对称轴.
的对称轴.
(2)当 时,将抛物线
时,将抛物线 向左平移2个单位,再向下平移1个单位,得到抛物线
向左平移2个单位,再向下平移1个单位,得到抛物线 .
.
①求抛物线 的解析式.
的解析式.
②设抛物线 与
与 轴交于
轴交于 ,
, 两点(点
两点(点 在点
在点 的右侧),与
的右侧),与 轴交于点
轴交于点 ,连接
,连接 .点
.点 为第一象限内抛物线
为第一象限内抛物线 上一动点,过点
上一动点,过点 作
作 于点
于点 .设点
.设点 的横坐标为
的横坐标为 .是否存在点
.是否存在点 ,使得以点
,使得以点 ,
, ,
, 为顶点的三角形与
为顶点的三角形与 相似,若存在,求出
相似,若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

 :
: 经过点
经过点 和
和 .
.(1)求抛物线
 的对称轴.
的对称轴.(2)当
 时,将抛物线
时,将抛物线 向左平移2个单位,再向下平移1个单位,得到抛物线
向左平移2个单位,再向下平移1个单位,得到抛物线 .
.①求抛物线
 的解析式.
的解析式.②设抛物线
 与
与 轴交于
轴交于 ,
, 两点(点
两点(点 在点
在点 的右侧),与
的右侧),与 轴交于点
轴交于点 ,连接
,连接 .点
.点 为第一象限内抛物线
为第一象限内抛物线 上一动点,过点
上一动点,过点 作
作 于点
于点 .设点
.设点 的横坐标为
的横坐标为 .是否存在点
.是否存在点 ,使得以点
,使得以点 ,
, ,
, 为顶点的三角形与
为顶点的三角形与 相似,若存在,求出
相似,若存在,求出 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
26.如图,在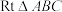 中,点
中,点 为斜边
为斜边 上一动点,将
上一动点,将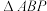 沿直线
沿直线 折叠,使得点
折叠,使得点 的对应点为
的对应点为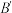 ,连接
,连接 ,
, ,
,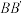 ,
, .
.
(1)如图①,若 ,证明:
,证明: .
.
(2)如图②,若 ,
, ,求
,求 的值.
的值.
(3)如图③,若 ,是否存在点
,是否存在点 ,使得
,使得 .若存在,求此时
.若存在,求此时 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.

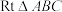 中,点
中,点 为斜边
为斜边 上一动点,将
上一动点,将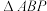 沿直线
沿直线 折叠,使得点
折叠,使得点 的对应点为
的对应点为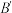 ,连接
,连接 ,
, ,
,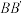 ,
, .
.(1)如图①,若
 ,证明:
,证明: .
.(2)如图②,若
 ,
, ,求
,求 的值.
的值.(3)如图③,若
 ,是否存在点
,是否存在点 ,使得
,使得 .若存在,求此时
.若存在,求此时 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
