全一卷
1.在 ,
, ,
, ,
,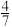 这四个数中,整数是( )
这四个数中,整数是( )
 ,
, ,
, ,
,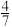 这四个数中,整数是( )
这四个数中,整数是( )A. | B. | C. | D.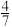 |
2.下列图形中,是中心对称图形,但不是轴对称图形的是( )
A. | B. |
C. | D. |
3.北京故宫的占地面积约为720 000m2,将720 000用科学记数法表示为( ).
| A.72×104 | B.7.2×105 | C.7.2×106 | D.0.72×106 |
4.下列说法正确的是( )
A. | B.若 取最小值,则 取最小值,则 |
C.若 ,则 ,则 | D.若 ,则 ,则 |
5.已知 ,则分式
,则分式 与
与 的大小关系是( )
的大小关系是( )
 ,则分式
,则分式 与
与 的大小关系是( )
的大小关系是( )A. | B. | C. | D.不能确定 |
6.已知反比例函数 ,当
,当 时,
时, 随
随 的增大而减小,那么一次的数
的增大而减小,那么一次的数 的图像经过第( )
的图像经过第( )
 ,当
,当 时,
时, 随
随 的增大而减小,那么一次的数
的增大而减小,那么一次的数 的图像经过第( )
的图像经过第( )| A.一,二,三象限 | B.一,二,四象限 |
| C.一,三,四象限 | D.二,三,四象限 |
7.一个儿何体由大小相同的小立方块搭成,从上面看到的几何体的形状图如图所示,其中小正方形中的数字表示在该位置的小正方块的个数,能正确表示该几何体的主视图的是( )


A. | B. | C. | D. |
8.如图, 是线段
是线段 上除端点外的一点,将
上除端点外的一点,将 绕正方形
绕正方形 的顶点
的顶点 顺时针旋转
顺时针旋转 ,得到
,得到 .连接
.连接 交
交 于点
于点 .下列结论正确的是( )
.下列结论正确的是( )

 是线段
是线段 上除端点外的一点,将
上除端点外的一点,将 绕正方形
绕正方形 的顶点
的顶点 顺时针旋转
顺时针旋转 ,得到
,得到 .连接
.连接 交
交 于点
于点 .下列结论正确的是( )
.下列结论正确的是( )
A. | B. | C. | D. |
9.小刚家2019年和2020年的家庭支出如下,已知2020年的总支出比2019年的总支出增加了2成,则下列说法正确的是( )


| A.2020年教育方面的支出是2019年教育方面的支出的1.4倍; |
| B.2020年衣食方面的支出比2019年衣食方面的支出增加了10%; |
| C.2020年总支出比2019年总支出增加了2%; |
| D.2020年其他方面的支出与2019年娱乐方面的支出相同. |
10.已知函数 ,则下列说法不正确的个数是( )
,则下列说法不正确的个数是( )
①若该函数图像与 轴只有一个交点,则
轴只有一个交点,则
②方程 至少有一个整数根
至少有一个整数根
③若 ,则
,则 的函数值都是负数
的函数值都是负数
④不存在实数 ,使得
,使得 对任意实数
对任意实数 都成立
都成立
 ,则下列说法不正确的个数是( )
,则下列说法不正确的个数是( )①若该函数图像与
 轴只有一个交点,则
轴只有一个交点,则
②方程
 至少有一个整数根
至少有一个整数根③若
 ,则
,则 的函数值都是负数
的函数值都是负数④不存在实数
 ,使得
,使得 对任意实数
对任意实数 都成立
都成立| A.0 | B.1 | C.2 | D.3 |
11.
________

12.已知 ,则
,则
________
 ,则
,则
13.一个圆柱形橡皮泥,底面积是 .高是
.高是 .如果用这个橡皮泥的一半,把它捏成高为
.如果用这个橡皮泥的一半,把它捏成高为 的圆锥,则这个圆锥的底面积是
的圆锥,则这个圆锥的底面积是______ 
 .高是
.高是 .如果用这个橡皮泥的一半,把它捏成高为
.如果用这个橡皮泥的一半,把它捏成高为 的圆锥,则这个圆锥的底面积是
的圆锥,则这个圆锥的底面积是
14.如图,3条直线两两相交最多有3个交点,4条直线两两相交最多有6个交点,按照这样的规律,则20条直线两两相交最多有______ 个交点


15.三个数3, 在数轴上从左到右依次排列,且以这三个数为边长能构成三角形,则
在数轴上从左到右依次排列,且以这三个数为边长能构成三角形,则 的取值范围为
的取值范围为______
 在数轴上从左到右依次排列,且以这三个数为边长能构成三角形,则
在数轴上从左到右依次排列,且以这三个数为边长能构成三角形,则 的取值范围为
的取值范围为16.如图,作 的任意一条直经
的任意一条直经 ,分别以
,分别以 为圆心,以
为圆心,以 的长为半径作弧,与
的长为半径作弧,与 相交于点
相交于点 和
和 ,顺次连接
,顺次连接 ,得到六边形
,得到六边形 ,则
,则 的面积与阴影区域的面积的比值为
的面积与阴影区域的面积的比值为______ ;

 的任意一条直经
的任意一条直经 ,分别以
,分别以 为圆心,以
为圆心,以 的长为半径作弧,与
的长为半径作弧,与 相交于点
相交于点 和
和 ,顺次连接
,顺次连接 ,得到六边形
,得到六边形 ,则
,则 的面积与阴影区域的面积的比值为
的面积与阴影区域的面积的比值为
17.某酒店客房都有三人间普通客房,双人间普通客房,收费标准为:三人间150元/间,双人间140元/间.为吸引游客,酒店实行团体入住五折优惠措施,一个46人的旅游团,优惠期间到该酒店入住,住了一些三人间普通客房和双人间普通客房,若每间客房正好住满,且一天共花去住宿费1310元,则该旅游团住了三人间普通客房和双人间普通客房共________ 间;
18.已知,如图1,若 是
是 中
中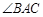 的内角平分线,通过证明可得
的内角平分线,通过证明可得 ,同理,若
,同理,若 是
是 中
中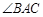 的外角平分线,通过探究也有类似的性质.请你根据上述信息,求解如下问题:如图2,在
的外角平分线,通过探究也有类似的性质.请你根据上述信息,求解如下问题:如图2,在 中,
中, 是
是 的内角平分线,则
的内角平分线,则 的
的 边上的中线长
边上的中线长 的取值范围是
的取值范围是________

 是
是 中
中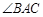 的内角平分线,通过证明可得
的内角平分线,通过证明可得 ,同理,若
,同理,若 是
是 中
中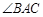 的外角平分线,通过探究也有类似的性质.请你根据上述信息,求解如下问题:如图2,在
的外角平分线,通过探究也有类似的性质.请你根据上述信息,求解如下问题:如图2,在 中,
中, 是
是 的内角平分线,则
的内角平分线,则 的
的 边上的中线长
边上的中线长 的取值范围是
的取值范围是
19.计算

20.先因式分解,再计算求值: ,其中
,其中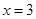 .
.
 ,其中
,其中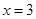 .
.21.解方程:

22.小明在 点测得
点测得 点在
点在 点的北偏西
点的北偏西 方向,并由
方向,并由 点向南偏西
点向南偏西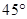 方向行走到达
方向行走到达 点测得
点测得 点在
点在 点的北偏西
点的北偏西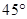 方向,继续向正西方向行走
方向,继续向正西方向行走 后到达
后到达 点,测得
点,测得 点在
点在 点的北偏东
点的北偏东 方向,求
方向,求 两点之间的距离.(结果保留
两点之间的距离.(结果保留 ,参数数据
,参数数据 )
)

 点测得
点测得 点在
点在 点的北偏西
点的北偏西 方向,并由
方向,并由 点向南偏西
点向南偏西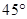 方向行走到达
方向行走到达 点测得
点测得 点在
点在 点的北偏西
点的北偏西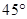 方向,继续向正西方向行走
方向,继续向正西方向行走 后到达
后到达 点,测得
点,测得 点在
点在 点的北偏东
点的北偏东 方向,求
方向,求 两点之间的距离.(结果保留
两点之间的距离.(结果保留 ,参数数据
,参数数据 )
)
23.如图①是甲,乙两个圆柱形水槽的轴截面示意图,乙槽中有一圆柱形实心铁块立放其中(圆柱形实心铁块的下底面完全落在乙槽底面上),现将甲槽中的水匀速注入乙槽,甲,乙两个水槽中水的深度 与注水时间
与注水时间 之间的关系如图②所示,根据图像解答下列问题:
之间的关系如图②所示,根据图像解答下列问题:

(1)图②中折线 表示_____________槽中水的深度与注入时间之间的关系;线段
表示_____________槽中水的深度与注入时间之间的关系;线段 表示_____________槽中水的深度与注入时间之间的关系;铁块的高度为_____________
表示_____________槽中水的深度与注入时间之间的关系;铁块的高度为_____________ .
.
(2)注入多长时间,甲、乙两个水槽中水的深度相同?(请写出必要的计算过程)
 与注水时间
与注水时间 之间的关系如图②所示,根据图像解答下列问题:
之间的关系如图②所示,根据图像解答下列问题:
(1)图②中折线
 表示_____________槽中水的深度与注入时间之间的关系;线段
表示_____________槽中水的深度与注入时间之间的关系;线段 表示_____________槽中水的深度与注入时间之间的关系;铁块的高度为_____________
表示_____________槽中水的深度与注入时间之间的关系;铁块的高度为_____________ .
.(2)注入多长时间,甲、乙两个水槽中水的深度相同?(请写出必要的计算过程)
24.如图,在平行四边形 中,
中, ,点
,点 为线段
为线段 的三等分点(靠近点
的三等分点(靠近点 ),点
),点 为线段
为线段 的三等分点(靠近点
的三等分点(靠近点 ,且
,且 .将
.将 沿
沿 对折,
对折, 边与
边与 边交于点
边交于点 ,且
,且 .
.

(1)证明:四边形 为矩形;
为矩形;
(2)求四边形 的面积.
的面积.
 中,
中, ,点
,点 为线段
为线段 的三等分点(靠近点
的三等分点(靠近点 ),点
),点 为线段
为线段 的三等分点(靠近点
的三等分点(靠近点 ,且
,且 .将
.将 沿
沿 对折,
对折, 边与
边与 边交于点
边交于点 ,且
,且 .
.
(1)证明:四边形
 为矩形;
为矩形;(2)求四边形
 的面积.
的面积.25.某校要从甲,乙两名学生中挑选一名学生参加数学竞赛,在最近的8次选拔赛中,他们的成绩(成绩均为整数,单位:分)如下:
甲:92,95,96,88,92,98,99,100
乙:100,87,92,93,9▆,95,97,98
由于保存不当,学生乙有一次成绩的个位数字模糊不清,
(1)求甲成绩的平均数和中位数;
(2)求事件“甲成绩的平均数大于乙成绩的平均数”的概率;
(3)当甲成绩的平均数与乙成绩的平均数相等时,请用方差大小说明应选哪个学生参加数学竞赛.
甲:92,95,96,88,92,98,99,100
乙:100,87,92,93,9▆,95,97,98
由于保存不当,学生乙有一次成绩的个位数字模糊不清,
(1)求甲成绩的平均数和中位数;
(2)求事件“甲成绩的平均数大于乙成绩的平均数”的概率;
(3)当甲成绩的平均数与乙成绩的平均数相等时,请用方差大小说明应选哪个学生参加数学竞赛.
26.如图,一次函数 的图象与
的图象与 轴的正半轴交于点
轴的正半轴交于点 ,与反比例函数
,与反比例函数 的图像交于
的图像交于 两点.以
两点.以 为边作正方形
为边作正方形 ,点
,点 落在
落在 轴的负半轴上,已知
轴的负半轴上,已知 的面积与
的面积与 的面积之比为
的面积之比为 .
.

(1)求一次函数 的表达式:
的表达式:
(2)求点 的坐标及
的坐标及 外接圆半径的长.
外接圆半径的长.
 的图象与
的图象与 轴的正半轴交于点
轴的正半轴交于点 ,与反比例函数
,与反比例函数 的图像交于
的图像交于 两点.以
两点.以 为边作正方形
为边作正方形 ,点
,点 落在
落在 轴的负半轴上,已知
轴的负半轴上,已知 的面积与
的面积与 的面积之比为
的面积之比为 .
.
(1)求一次函数
 的表达式:
的表达式:(2)求点
 的坐标及
的坐标及 外接圆半径的长.
外接圆半径的长.27.如图,已知 是
是 的直径.
的直径. 是
是 的弦,弦
的弦,弦 垂直
垂直 于点
于点 ,交
,交 于点
于点 .过点
.过点 作
作 的切线交
的切线交 的延长线于点
的延长线于点

(1)求证: ;
;
(2)判断 是否成立?若成立,请证明该结论;
是否成立?若成立,请证明该结论;
(3)若 为
为 中点,
中点, ,
, ,求
,求 的长.
的长.
 是
是 的直径.
的直径. 是
是 的弦,弦
的弦,弦 垂直
垂直 于点
于点 ,交
,交 于点
于点 .过点
.过点 作
作 的切线交
的切线交 的延长线于点
的延长线于点

(1)求证:
 ;
;(2)判断
 是否成立?若成立,请证明该结论;
是否成立?若成立,请证明该结论;(3)若
 为
为 中点,
中点, ,
, ,求
,求 的长.
的长.28.如图,抛物线 与
与 轴交于除原点
轴交于除原点 和点
和点 ,且其顶点
,且其顶点 关于
关于 轴的对称点坐标为
轴的对称点坐标为 .
.

(1)求抛物线的函数表达式;
(2)抛物线的对称轴上存在定点 ,使得抛物线
,使得抛物线 上的任意一点
上的任意一点 到定点
到定点 的距离与点
的距离与点 到直线
到直线 的距离总相等.
的距离总相等.
①证明上述结论并求出点 的坐标;
的坐标;
②过点 的直线
的直线 与抛物线
与抛物线 交于
交于 两点.证明:当直线
两点.证明:当直线 绕点
绕点 旋转时,
旋转时, 是定值,并求出该定值;
是定值,并求出该定值;
(3)点 是该抛物线上的一点,在
是该抛物线上的一点,在 轴,
轴, 轴上分别找点
轴上分别找点 ,使四边形
,使四边形 周长最小,直接写出
周长最小,直接写出 的坐标.
的坐标.
 与
与 轴交于除原点
轴交于除原点 和点
和点 ,且其顶点
,且其顶点 关于
关于 轴的对称点坐标为
轴的对称点坐标为 .
.
(1)求抛物线的函数表达式;
(2)抛物线的对称轴上存在定点
 ,使得抛物线
,使得抛物线 上的任意一点
上的任意一点 到定点
到定点 的距离与点
的距离与点 到直线
到直线 的距离总相等.
的距离总相等.①证明上述结论并求出点
 的坐标;
的坐标;②过点
 的直线
的直线 与抛物线
与抛物线 交于
交于 两点.证明:当直线
两点.证明:当直线 绕点
绕点 旋转时,
旋转时, 是定值,并求出该定值;
是定值,并求出该定值;(3)点
 是该抛物线上的一点,在
是该抛物线上的一点,在 轴,
轴, 轴上分别找点
轴上分别找点 ,使四边形
,使四边形 周长最小,直接写出
周长最小,直接写出 的坐标.
的坐标. 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
