全一卷
1. 的倒数是( )
的倒数是( )
 的倒数是( )
的倒数是( )A. | B. | C.2 | D.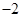 |
2.下列计算正确的是( )
A. | B. |
C. | D. |
3.为迎接中国共产党建党一百周年,某班50名同学进行了党史知识竞赛,测试成绩统计如下表,其中有两个数据被遮盖.
下列关于成绩的统计量中,与被遮盖的数据无关的是( )
成绩/分 | 91 | 92 | 93 | 94 | 95 | 96 | 97 | 98 | 99 | 100 |
人数 | ■ | ■ | 1 | 2 | 3 | 5 | 6 | 8 | 10 | 12 |
下列关于成绩的统计量中,与被遮盖的数据无关的是( )
| A.平均数,方差 | B.中位数,方差 |
| C.中位数,众数 | D.平均数,众数 |
4.关于x的一元二次方程 的根的情况,下列说法正确的是( )
的根的情况,下列说法正确的是( )
 的根的情况,下列说法正确的是( )
的根的情况,下列说法正确的是( )| A.有两个不相等的实数根 | B.有两个相等的实数根 |
| C.无实数根 | D.无法确定 |
5.如图,是由若干个相同的小正方形搭成的一个几何体的主视图和左视图,则组成这个几何体的小正方形的个数不可能是( )


| A.3 | B.4 | C.5 | D.6 |
6.随着互联网技术的发展,我国快递业务量逐年增加,据统计从2018年到2020年,我国快递业务量由507亿件增加到833.6亿件,设我国从2018年到2020年快递业务量的年平均增长率为x,则可列方程为( )
A. | B. |
C. | D. |
7.如图,在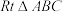 中,
中,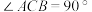 ,根据尺规作图的痕迹,判断以下结论错误的是( )
,根据尺规作图的痕迹,判断以下结论错误的是( )

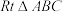 中,
中,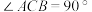 ,根据尺规作图的痕迹,判断以下结论错误的是( )
,根据尺规作图的痕迹,判断以下结论错误的是( )
A. | B. |
C. | D. |
8.定义:一次函数 的特征数为
的特征数为 ,若一次函数
,若一次函数 的图象向上平移3个单位长度后与反比例函数
的图象向上平移3个单位长度后与反比例函数 的图象交于A,B两点,且点A,B关于原点对称,则一次函数
的图象交于A,B两点,且点A,B关于原点对称,则一次函数 的特征数是( )
的特征数是( )
 的特征数为
的特征数为 ,若一次函数
,若一次函数 的图象向上平移3个单位长度后与反比例函数
的图象向上平移3个单位长度后与反比例函数 的图象交于A,B两点,且点A,B关于原点对称,则一次函数
的图象交于A,B两点,且点A,B关于原点对称,则一次函数 的特征数是( )
的特征数是( )A. | B. | C. | D. |
9.如图,已知 ,
, ,
, ,点E为射线
,点E为射线 上一个动点,连接
上一个动点,连接 ,将
,将 沿
沿 折叠,点B落在点
折叠,点B落在点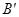 处,过点
处,过点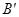 作
作 的垂线,分别交
的垂线,分别交 ,
, 于M,N两点,当
于M,N两点,当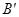 为线段
为线段 的三等分点时,
的三等分点时,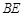 的长为( )
的长为( )

 ,
, ,
, ,点E为射线
,点E为射线 上一个动点,连接
上一个动点,连接 ,将
,将 沿
沿 折叠,点B落在点
折叠,点B落在点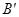 处,过点
处,过点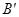 作
作 的垂线,分别交
的垂线,分别交 ,
, 于M,N两点,当
于M,N两点,当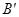 为线段
为线段 的三等分点时,
的三等分点时,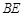 的长为( )
的长为( )
A. | B. | C. 或 或 | D. 或 或 |
10.如图,在矩形 中,
中, ,
, ,动点P,Q同时从点A出发,点P沿A→B→C的路径运动,点Q沿A→D→C的路径运动,点P,Q的运动速度相同,当点P到达点C时,点Q也随之停止运动,连接
,动点P,Q同时从点A出发,点P沿A→B→C的路径运动,点Q沿A→D→C的路径运动,点P,Q的运动速度相同,当点P到达点C时,点Q也随之停止运动,连接 .设点P的运动路程为x,
.设点P的运动路程为x, 为y,则y关于x的函数图象大致是( )
为y,则y关于x的函数图象大致是( )

 中,
中, ,
, ,动点P,Q同时从点A出发,点P沿A→B→C的路径运动,点Q沿A→D→C的路径运动,点P,Q的运动速度相同,当点P到达点C时,点Q也随之停止运动,连接
,动点P,Q同时从点A出发,点P沿A→B→C的路径运动,点Q沿A→D→C的路径运动,点P,Q的运动速度相同,当点P到达点C时,点Q也随之停止运动,连接 .设点P的运动路程为x,
.设点P的运动路程为x, 为y,则y关于x的函数图象大致是( )
为y,则y关于x的函数图象大致是( )
A. | B. | C. | D. |
11.冠状病毒是一类病毒的总称,其最大直径约为0.00000012米,数据0.00000012科学记数法表示为__________ .
12.如图所示,电路连接完好,且各元件工作正常随机闭合开关 ,
, ,
, 中的两个,能让两个小灯泡同时发光的概率是
中的两个,能让两个小灯泡同时发光的概率是__________ .

 ,
, ,
, 中的两个,能让两个小灯泡同时发光的概率是
中的两个,能让两个小灯泡同时发光的概率是
13.一副三角板如图所示摆放,且 ,则
,则 的度数为
的度数为__________ .

 ,则
,则 的度数为
的度数为
14.我国古代数学著作《增删算法统宗》记载“绳索量竿”问题:“一条竿子一条索,索比竿子长一托.折回索子却量竿,却比竿子短一托.”其大意为:现有一根竿和一条绳索,用绳索去量竿,绳索比竿长5尺;如果将绳索对半折后再去量竿,就比竿短5尺.设绳索长 尺,竿长
尺,竿长 尺,则符合题意的方程组是
尺,则符合题意的方程组是________________________
 尺,竿长
尺,竿长 尺,则符合题意的方程组是
尺,则符合题意的方程组是15.若关于x的不等式组 ,有且只有2个整数解,则a的取值范围是
,有且只有2个整数解,则a的取值范围是__________ .
 ,有且只有2个整数解,则a的取值范围是
,有且只有2个整数解,则a的取值范围是16.如图, 是⊙O的弦,
是⊙O的弦, ,点C是⊙O上的一个动点,且
,点C是⊙O上的一个动点,且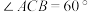 ,若点M,N分别是
,若点M,N分别是 ,
, 的中点,则图中阴影部分面积的最大值是
的中点,则图中阴影部分面积的最大值是__________ .

 是⊙O的弦,
是⊙O的弦, ,点C是⊙O上的一个动点,且
,点C是⊙O上的一个动点,且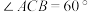 ,若点M,N分别是
,若点M,N分别是 ,
, 的中点,则图中阴影部分面积的最大值是
的中点,则图中阴影部分面积的最大值是
17.如图, ,
, ,
, …,
…, 都是斜边在x轴上的等腰直角三角形,点
都是斜边在x轴上的等腰直角三角形,点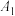 ,
, ,
, ,…,
,…, 都在x轴上,点
都在x轴上,点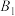 ,
,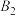 ,
, ,…,
,…, 都在反比例函数
都在反比例函数 的图象上,则点
的图象上,则点 的坐标为
的坐标为__________ .(用含有正整数n的式子表示)

 ,
, ,
, …,
…, 都是斜边在x轴上的等腰直角三角形,点
都是斜边在x轴上的等腰直角三角形,点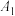 ,
, ,
, ,…,
,…, 都在x轴上,点
都在x轴上,点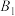 ,
,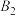 ,
, ,…,
,…, 都在反比例函数
都在反比例函数 的图象上,则点
的图象上,则点 的坐标为
的坐标为
18.计算;


19.先化简,再求值:
 ,其中x满足
,其中x满足 .
.
 ,其中x满足
,其中x满足 .
.20.如图,甲、乙两个转盘均被分成3个面积相等的扇形,每个扇形中都标有相应的数字,同时转动两个转盘(当指针指在边界线上时视为无效,需重新转动转盘),当转盘停止后,把甲、乙两个转盘中指针所指数字分别记为x,y.请用树状图或列表法求点 落在平面直角坐标系第一象限内的概率.
落在平面直角坐标系第一象限内的概率.

 落在平面直角坐标系第一象限内的概率.
落在平面直角坐标系第一象限内的概率.
21.如图,一段河流自西向东,河岸笔直,且两岸平行,为测量其宽度,小明在南岸边B处测得对岸边A处一棵大树位于北偏东60°方向,他以 的速度沿着河岸向东步行
的速度沿着河岸向东步行 后到达C处,此时测得大树位于北偏东45°方向,试计算此段河面的宽度(结果取整数,参考数据:
后到达C处,此时测得大树位于北偏东45°方向,试计算此段河面的宽度(结果取整数,参考数据: )
)

 的速度沿着河岸向东步行
的速度沿着河岸向东步行 后到达C处,此时测得大树位于北偏东45°方向,试计算此段河面的宽度(结果取整数,参考数据:
后到达C处,此时测得大树位于北偏东45°方向,试计算此段河面的宽度(结果取整数,参考数据: )
)
22.暑期将至,某校组织学生进行“防漏水”安全知识竞赛,老师从中随机抽取了部分学生的成绩(得分取整数,满分为100分),整理后绘制成如图所示的不完整的扇形统计图和频数分布直方图.
测试成绩扇形统计图.

测试成绩频数分布直方图

其中A组的频数a比B组的频数b小15.请根据以上信息,解答下列问题:
(1)本次共抽取__________名学生,a的值为__________;
(2)在扇形统计图中,n=__________,E组所占比例为__________%;
(3)补全频数分布直方图;
(4)若全校共有1500名学生,请根据抽样调查的结果,估计成绩在80分以上的学生人数.
测试成绩扇形统计图.

测试成绩频数分布直方图

其中A组的频数a比B组的频数b小15.请根据以上信息,解答下列问题:
(1)本次共抽取__________名学生,a的值为__________;
(2)在扇形统计图中,n=__________,E组所占比例为__________%;
(3)补全频数分布直方图;
(4)若全校共有1500名学生,请根据抽样调查的结果,估计成绩在80分以上的学生人数.
23.为做好新冠疫情的防控工作,某单位需购买甲、乙两种消毒液经了解每桶甲种消毒液的零售价比乙种消毒液的零售价多6元,该单位以零售价分别用900元和720元采购了相同桶数的甲、乙两种消毒液.
(1)求甲、乙两种消毒液的零售价分别是每桶多少元?
(2)由于疫情防控进入常态化,该单位需再次购买两种消毒液共300桶,且甲种消毒液的桶数不少于乙种消毒液桶数的 ,由于购买量大,甲、乙两种消毒液分别获得了20元/桶,15元/桶的批发价.求甲种消毒液购买多少桶时,所需资金总额最少?最少总金额是多少元?
,由于购买量大,甲、乙两种消毒液分别获得了20元/桶,15元/桶的批发价.求甲种消毒液购买多少桶时,所需资金总额最少?最少总金额是多少元?
(1)求甲、乙两种消毒液的零售价分别是每桶多少元?
(2)由于疫情防控进入常态化,该单位需再次购买两种消毒液共300桶,且甲种消毒液的桶数不少于乙种消毒液桶数的
 ,由于购买量大,甲、乙两种消毒液分别获得了20元/桶,15元/桶的批发价.求甲种消毒液购买多少桶时,所需资金总额最少?最少总金额是多少元?
,由于购买量大,甲、乙两种消毒液分别获得了20元/桶,15元/桶的批发价.求甲种消毒液购买多少桶时,所需资金总额最少?最少总金额是多少元?24.如图, 是⊙O的直径,过点A作⊙O的切线
是⊙O的直径,过点A作⊙O的切线 ,点P是射线
,点P是射线 上的动点,连接
上的动点,连接 ,过点B作
,过点B作 ,交⊙O于点D,连接
,交⊙O于点D,连接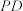 .
.

(1)求证: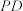 是⊙O的切线
是⊙O的切线
(2)当四边形 是平行四边形时,求
是平行四边形时,求 的度数.
的度数.
 是⊙O的直径,过点A作⊙O的切线
是⊙O的直径,过点A作⊙O的切线 ,点P是射线
,点P是射线 上的动点,连接
上的动点,连接 ,过点B作
,过点B作 ,交⊙O于点D,连接
,交⊙O于点D,连接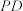 .
.
(1)求证:
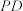 是⊙O的切线
是⊙O的切线(2)当四边形
 是平行四边形时,求
是平行四边形时,求 的度数.
的度数.25.已知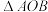 和
和 都是等腰直角三角形
都是等腰直角三角形 ,
, .
.
(1)如图1,连接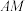 ,
, ,求证:
,求证: ;
;
(2)将 绕点O顺时针旋转.
绕点O顺时针旋转.
①如图2,当点M恰好在 边上时,求证:
边上时,求证: ;
;
②当点A,M,N在同一条直线上时,若 ,
, ,请直接写出线段
,请直接写出线段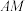 的长.
的长.


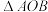 和
和 都是等腰直角三角形
都是等腰直角三角形 ,
, .
.(1)如图1,连接
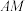 ,
, ,求证:
,求证: ;
;(2)将
 绕点O顺时针旋转.
绕点O顺时针旋转.①如图2,当点M恰好在
 边上时,求证:
边上时,求证: ;
;②当点A,M,N在同一条直线上时,若
 ,
, ,请直接写出线段
,请直接写出线段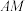 的长.
的长.

26.如图,抛物线 交x轴于
交x轴于 ,
, 两点,交y轴于点C,动点P在抛物线的对称轴上.
两点,交y轴于点C,动点P在抛物线的对称轴上.
(1)求抛物线的解析式;
(2)当以P,B,C为顶点的三角形周长最小时,求点P的坐标及 的周长;
的周长;
(3)若点Q是平面直角坐标系内的任意一点,是否存在点Q,使得以A,C,P,Q为顶点的四边形是菱形?若存在,请直接写出所有符合条件的点Q的坐标;若不存在,请说明理由.

 交x轴于
交x轴于 ,
, 两点,交y轴于点C,动点P在抛物线的对称轴上.
两点,交y轴于点C,动点P在抛物线的对称轴上.(1)求抛物线的解析式;
(2)当以P,B,C为顶点的三角形周长最小时,求点P的坐标及
 的周长;
的周长;(3)若点Q是平面直角坐标系内的任意一点,是否存在点Q,使得以A,C,P,Q为顶点的四边形是菱形?若存在,请直接写出所有符合条件的点Q的坐标;若不存在,请说明理由.

 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
