搜索
全一卷
难度系数：0.94 
答案解析
有奖纠错
1．四个数-3.14，0，1，2中为负数的是（ ）
| A．-3.14 | B．0 | C．1 | D．2 |
2．把一个正六棱柱如图摆放，光线由上向下照射此正六棱柱时的正投影是( )
A． | B． | C． | D． |
3．袋子中装有10个黑球、1个白球，它们除颜色外无其他差别，随机从袋子中摸出一个球，则（）
| A．这个球一定是黑球 | B．摸到黑球、白球的可能性的大小一样 |
| C．这个球可能是白球 | D．事先能确定摸到什么颜色的球 |
4．若代数式x＋2的值为1，则x等于( )
| A．1 | B．－1 | C．3 | D．－3 |
5．如图，在△ABC和△DEF中，∠B＝∠DEF，AB＝DE，若添加下列一个条件后，仍然不能证明△ABC≌△DEF，则这个条件是( )
| A．∠A＝∠D | B．BC＝EF | C．∠ACB＝∠F | D．AC＝DF |
6．如图，AB∥CD，∠B=68°，∠E=20°，则∠D的度数为（ ）
| A．28° | B．38° | C．48° | D．88° |
7．如图，点A的坐标（﹣1，2），点A关于y轴的对称点的坐标为（ ）
| A．（1，2） | B．（﹣1，﹣2） | C．（1，﹣2） | D．（2，﹣1） |
8．已知关于x的一元二次方程
有两个相等的实数根，则a的值是（ ）
有两个相等的实数根，则a的值是（ ）| A．4 | B．﹣4 | C．1 | D．﹣1 |
9．如图，在
中，BC=4，AC=3，
则
的值为（ ）
中，BC=4，AC=3，
则
的值为（ ）
A． | B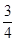． | C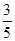． | D． |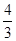
10．如图，正方形ABCD的边长为4，P为正方形边上一动点，运动路线是A→D→C→B→A,设P点经过的路程为x，以点A、P、D为顶点的三角形的面积是y.则下列图象能大致反映y与x的函数关系的是( )
A． | B． | C． | D． |
11．若二次根式
有意义，则x的取值范围是 ▲ ．
有意义，则x的取值范围是 ▲ ．12．不等式
的解集是________ ．
的解集是13．因式分解：m3n﹣9mn＝______ ．
14．如图，在四边形ABCD中，AB=BC=CD=DA，对角线AC与BD相交于点O．若不增加任何字母与辅助线，要使得四边形ABCD是正方形，则还需添加的一个条件是_______ ．
15．如图是李大妈跳舞用的扇子，这个扇形AOB的圆心角∠O=120°，半径OA=3，则弧AB的长度为 （结果保留π）．
16．二次函数y＝x2－2x＋3的图象向左平移一个单位，再向上平移两个单位后，所得二次函数的解析式为_______________．
17．如图，在平面直角坐标系中，将
绕点O逆时针旋转60°后得到
，依此方式，绕点O连接旋转20次得到
，如果点A的坐标为（1，
），那么点
的坐标为_______．
绕点O逆时针旋转60°后得到
，依此方式，绕点O连接旋转20次得到
，如果点A的坐标为（1，
），那么点
的坐标为_______．
18．计算：
．
．19．两个城镇A，B与一条公路CD，一条河流CE的位置如图所示，某人要修建一避暑山庄，要求该山庄到A，B的距离必须相等，到CD和CE的距离也必须相等，且在∠DCE的内部，请画出该山庄的位置P．（不要求写作法，保留作图痕迹．）
20．先化简，再求值：
，其中
，其中
21．某单位750名职工积极参加向贫困地区学校捐书活动，为了解职工的捐数量，采用随机抽样的方法抽取30名职工作为样本，对他们的捐书量进行统计，统计结果共有4本、5本、6本、7本、8本五类，分别用A、B、C、D、E表示，根据统计数据绘制成了如图所示的不完整的条形统计图，由图中给出的信息解答下列问题：
（1）补全条形统计图；
（2）求这30名职工捐书本数的平均数、众数和中位数；
（3）估计该单位750名职工共捐书多少本？
（1）补全条形统计图；
（2）求这30名职工捐书本数的平均数、众数和中位数；
（3）估计该单位750名职工共捐书多少本？
22．如图，在△ABC中，AD⊥BC，BE⊥AC，垂足分别为D，E，AD与BE相交于点F．
（1）求证：△ACD∽△BFD；
（2）当tan∠ABD=1，AC=3时，求BF的长．
（1）求证：△ACD∽△BFD；
（2）当tan∠ABD=1，AC=3时，求BF的长．
23．如图，某反比例函数图象的一支经过点A（2，3）和点B（点B在点A的右侧），作BC⊥y轴，垂足为点C，连结AB，AC．
（1）求该反比例函数的解析式；
（2）若△ABC的面积为6，求直线AB的表达式．
（1）求该反比例函数的解析式；
（2）若△ABC的面积为6，求直线AB的表达式．
24．如图，AB是⊙O的直径，弦CD⊥AB，垂足为H，连结AC，过
上一点E作EG∥AC交CD的延长线于点G，连结AE交CD于点F，且EG=FG，连结CE．
（1）求证：△ECF∽△GCE；
（2）求证：EG是⊙O的切线；
（3）延长AB交GE的延长线于点M，若tanG =
，AH=3
，求EM的值．
上一点E作EG∥AC交CD的延长线于点G，连结AE交CD于点F，且EG=FG，连结CE．（1）求证：△ECF∽△GCE；
（2）求证：EG是⊙O的切线；
（3）延长AB交GE的延长线于点M，若tanG =
，AH=3，求EM的值．25．已知：把Rt△ABC和Rt△DEF按如图（1）摆放（点C与点E重合），点B、C（E）、F在同一条直线上．∠ACB = ∠EDF = 90°，∠DEF = 45°，AC =" 8" cm，BC =" 6" cm，EF =" 9" cm．
如图（2），△DEF从图（1）的位置出发，以1 cm/s的速度沿CB向△ABC匀速移动，在△DEF移动的同时，点P从△ABC的顶点B出发，以2 cm/s的速度沿BA向点A匀速移动.当△DEF的顶点D移动到AC边上时，△DEF停止移动，点P也随之停止移动．DE与AC相交于点Q，连接PQ，设移动时间为t（s）（0＜t＜4.5）．
解答下列问题：
（1）当t为何值时，点A在线段PQ的垂直平分线上？
（2）连接PE，设四边形APEC的面积为y（cm2），求y与t之间的函数关系式；是否存在某一时刻t，使面积y最小？若存在，求出y的最小值；若不存在，说明理由．
（3）是否存在某一时刻t，使P、Q、F三点在同一条直线上？若存在，求出此时t的值；若不存在，说明理由．
如图（2），△DEF从图（1）的位置出发，以1 cm/s的速度沿CB向△ABC匀速移动，在△DEF移动的同时，点P从△ABC的顶点B出发，以2 cm/s的速度沿BA向点A匀速移动.当△DEF的顶点D移动到AC边上时，△DEF停止移动，点P也随之停止移动．DE与AC相交于点Q，连接PQ，设移动时间为t（s）（0＜t＜4.5）．
解答下列问题：
（1）当t为何值时，点A在线段PQ的垂直平分线上？
（2）连接PE，设四边形APEC的面积为y（cm2），求y与t之间的函数关系式；是否存在某一时刻t，使面积y最小？若存在，求出y的最小值；若不存在，说明理由．
（3）是否存在某一时刻t，使P、Q、F三点在同一条直线上？若存在，求出此时t的值；若不存在，说明理由．
