搜索
全一卷
难度系数：0.94 
答案解析
有奖纠错
1．2019的倒数是（ ）
| A．2019 | B． | C． | D． |
2．下列运算正确的是
| A．x•x2=x2 | B．（xy）2=xy2 | C．（x2）3=x6 | D．x2+x2=x4 |
3．一组数据1，1，4，3，6的平均数和众数分别是（）
| A．1，3 | B．3，1 | C．3，3 | D．3，4 |
4．一元二次方程x2+2x﹣4＝0的根的情况为（ ）
| A．没有实数根 | B．有两个相等的实数根 |
| C．有两个不相等的实数根 | D．无法确定 |
5．若两个相似多边形的面积之比为1：4，则它们的周长之比为（ ）
| A．1：4 | B．1：2 | C．2：1 | D．1：16 |
6．如图，点O在直线AB上且OC⊥OD，若∠COA=36°则∠DOB的大小为（ ）
| A．36° | B．54° | C．64° | D．72° |
7．在平面直角坐标系中，点P（2，3）关于x轴的对称点坐标为（）
| A．（﹣2，3） | B．（2，﹣3） | C．（3，﹣2） | D．（﹣2，﹣3） |
8．已知平行四边形ABCD中，∠B=4 ∠A，则∠C= （ ）
| A．18° | B．72° | C．36° | D．144° |
9．如图，在边长为1的小正方形组成的网格中，△ABC的三个顶点均在格点上，则tanA＝( )
A． | B． | C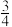． | D． |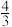
10．某人匀速跑步到公园，在公园里某处停留了一段时间，再沿原路匀速步行回家，此人离家的距离y与时间x的关系的大致图象是
A． | B． | C． | D． |
11．4的平方根是_______ ．
12．二次函数y＝2（x﹣5）2+3的顶点坐标是_____ ．
13．3x﹣1≤3﹣x的解集是_____．
14．菱形的两条对角线的长分别为6和8，则这个菱形的周长为_____ ．
15．已知圆柱体的底面半径为3cm，高为4cm，则圆柱体的侧面积为_____ ．
16．如图，在平面直角坐标系中，菱形OABC的一个顶点在原点O处，且∠AOC=60°，A点的坐标是（0，4），则直线AC的表达式是_____ ．
17．如图，把正方形纸片ABCD沿对边中点所在的直线对折后展开，折痕为MN，再过点B折叠纸片，使点A落在MN上的点F处，折痕为BE．若AB的长为2，则FM的长为___ ．
18．计算：
+（
）﹣1﹣20190．
+（
）﹣1﹣20190．19．先化简，再求值：
,其中
．
,其中
．20．如图，在△ABC中，AB＝AC，∠ABC＝72°．
（1）用直尺和圆规作∠ABC的平分线BD交AC于点D；（保留作图痕迹，不要求写作法）
（2）在（1）中作出∠ABC的平分线BD后，求∠ADB的度数．
（1）用直尺和圆规作∠ABC的平分线BD交AC于点D；（保留作图痕迹，不要求写作法）
（2）在（1）中作出∠ABC的平分线BD后，求∠ADB的度数．
21．（2014广州）从广州到某市，可乘坐普通列车或高铁，已知高铁的行驶路程是400千米，普通列车的行驶路程是高铁的行驶路程的1.3倍.
（1）求普通列车的行驶路程；
（2）若高铁的平均速度（千米/时）是普通列车平均速度（千米/时）的2.5倍，且乘坐高铁所需要时间比乘坐普通列车所需时间缩短3小时，求高铁的平均速度.
（1）求普通列车的行驶路程；
（2）若高铁的平均速度（千米/时）是普通列车平均速度（千米/时）的2.5倍，且乘坐高铁所需要时间比乘坐普通列车所需时间缩短3小时，求高铁的平均速度.
22．如图，在▱ABCD中，DE⊥AB，BF⊥CD，垂足分别为E，F，
（1）求证：△ADE≌△CBF；
（2）求证：四边形BFDE为矩形．
（1）求证：△ADE≌△CBF；
（2）求证：四边形BFDE为矩形．
23．某校为了解九年级学生2020年适应性考试数学成绩，现从九年级学生中随机抽取部分学生的适应性考试数学成绩，按A，B，C，D四个等级进行统计，并将统计结果绘制成如图所示不完整的统计图．请根据统计图中的信息解答下列问题：
（1）此次抽查的学生人数为 ；
（2）把条形统计图和扇形统计图补充完整；
（3）若该校九年级有学生1200人．请估计在这次适应性考试中达到B等级以上（含B等级）的人数．
（1）此次抽查的学生人数为 ；
（2）把条形统计图和扇形统计图补充完整；
（3）若该校九年级有学生1200人．请估计在这次适应性考试中达到B等级以上（含B等级）的人数．
24．如图，在△ABC中，AB＝AC，以AB为直径作圆O，分别交BC于点D，交CA的延长线于点E，过点D作DH⊥AC于点H，连接DE交线段OA于点F．
（1）求证：DH是圆O的切线；（2）若A为EH的中点，求
的值；（3）若EA＝EF＝1，求圆O的半径．
（1）求证：DH是圆O的切线；（2）若A为EH的中点，求
的值；（3）若EA＝EF＝1，求圆O的半径．25．如图：抛物线
与x轴交于A、B两点（点A在点B的左侧），与y轴交于点
与x轴交于A、B两点（点A在点B的左侧），与y轴交于点A．点P为线段BC上一点，过点P作直线ι⊥x轴于点F，交抛物线 于点 | B． （1）求A、B、C三点的坐标； （2）当点P在线段BC上运动时，求线段PE长的最大值； （3）当PE取最大值时，把抛物线 向右平移得到抛物线 ，抛物线与线段BE交于点M，若直线CM把△BCE的面积分为1：2两部分，则抛物线应向右平移几个单位长度可得到抛物线？ |
