全一卷
1. 的倒数是( )
的倒数是( )
 的倒数是( )
的倒数是( )| A.-2 | B.2 | C. | D. |
2.国家发改委2月7日紧急下达第二批中央预算内投资2亿元人民币,专项补助湖北多家医院的重症治疗病区建设,其中数据2亿元用科学记数法表示为( )
| A.2×107元 | B.2×108元 | C.2×109元 | D.0.2×109元 |
3.如图是由一个长方体和一个球组成的几何体,它的主视图是( ).


A. | B. | C. | D. |
4.如图,直线 //
//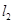 ,
, 于点
于点 ,
, .则
.则 的度数为( )
的度数为( )

 //
//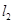 ,
, 于点
于点 ,
, .则
.则 的度数为( )
的度数为( )
A. | B.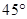 | C. | D. |
5.下列运算正确的是( )
A. | B.-(3ab)2=9a2b2 |
C. | D. |
6.如图, 是
是 的直径,
的直径, ,
, 是
是 上的两点,且
上的两点,且 平分
平分 ,
, 分别与
分别与 ,
, 相交于点
相交于点 ,
, ,则下列结论不一定成立的是( )
,则下列结论不一定成立的是( )

 是
是 的直径,
的直径, ,
, 是
是 上的两点,且
上的两点,且 平分
平分 ,
, 分别与
分别与 ,
, 相交于点
相交于点 ,
, ,则下列结论不一定成立的是( )
,则下列结论不一定成立的是( )
A. | B. | C. | D. |
7.小明同学10个周综合素质评价成绩统计如下:
这10个周的综合素质评价成绩的众数和方差分别是( )
| 成绩(分) | 94 | 95 | 97 | 98 | 100 |
| 周数(个) | 1 | 2 | 2 | 4 | 1 |
这10个周的综合素质评价成绩的众数和方差分别是( )
| A.97.5,2.8 | B.97,3 | C.98,2.8 | D.98,3 |
8.把不等式组 的解集表示在数轴上,正确的是( )
的解集表示在数轴上,正确的是( )
 的解集表示在数轴上,正确的是( )
的解集表示在数轴上,正确的是( )A. | B. |
C. | D. |
9.小明和同学做“抛掷质地均匀的硬币试验”获得的数据如下表
若抛掷硬币的次数为1000,则“正面朝上”的频数最接近( )
| 抛掷次数 | 100 | 200 | 300 | 400 | 500 |
| 正面朝上的频数 | 53 | 98 | 156 | 202 | 249 |
若抛掷硬币的次数为1000,则“正面朝上”的频数最接近( )
| A.200 | B.300 | C.400 | D.500 |
10.如图物体由两个圆锥组成.其主视图中, ,
, ,若上面圆锥的侧面积为
,若上面圆锥的侧面积为 ,则下面圆锥的侧面积为( )
,则下面圆锥的侧面积为( )

 ,
, ,若上面圆锥的侧面积为
,若上面圆锥的侧面积为 ,则下面圆锥的侧面积为( )
,则下面圆锥的侧面积为( )
| A.2 | B. | C.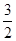 | D. |
11.世界文化遗产“三孔”景区已经完成5G幕站布设,“孔夫子家”自此有了5G网络.5G网络峰值速率为4G网络峰值速率的10倍,在峰值速率下传输600兆数据,5G网络比4G网络快50秒,求这两种网络的峰值速率.设5G网络的峰值速率为每秒传输 兆数据,依题意,可列方程是( )
兆数据,依题意,可列方程是( )
 兆数据,依题意,可列方程是( )
兆数据,依题意,可列方程是( )A. | B. |
C. | D. |
12.如图,把矩形 沿
沿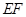 翻折,点
翻折,点 恰好落在
恰好落在 边的
边的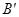 处,若
处,若 ,
, ,
, ,则矩形
,则矩形 的面积是( )
的面积是( )

 沿
沿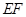 翻折,点
翻折,点 恰好落在
恰好落在 边的
边的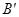 处,若
处,若 ,
, ,
, ,则矩形
,则矩形 的面积是( )
的面积是( )
A. | B. | C. | D.16 |
13.如图,在平行四边形 中,
中, ,
, 于
于 ,
, 于
于 ,
, ,
, 相交于
相交于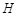 ,
, 与
与 的延长线相交于点
的延长线相交于点 ,下面给出四个结论:①
,下面给出四个结论:① ;②
;② ;③
;③ ;④
;④ ,其中正B确的结论是( )
,其中正B确的结论是( )

 中,
中, ,
, 于
于 ,
, 于
于 ,
, ,
, 相交于
相交于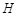 ,
, 与
与 的延长线相交于点
的延长线相交于点 ,下面给出四个结论:①
,下面给出四个结论:① ;②
;② ;③
;③ ;④
;④ ,其中正B确的结论是( )
,其中正B确的结论是( )
| A.①②③ | B.②④ | C.②③④ | D.①②③④ |
14.如图,若 内一点
内一点 满足
满足 ,则点
,则点 为
为 的布洛卡点,三角形的布洛卡点由法国数学家和数学教育家克洛尔于1816年首次发现,但他的发现并未被当时的人们所注意.1875年,布洛卡点被一个数学爱好者法国军官布洛卡重新发现,并用他的名字命名.问题:已知等腰直角三角形
的布洛卡点,三角形的布洛卡点由法国数学家和数学教育家克洛尔于1816年首次发现,但他的发现并未被当时的人们所注意.1875年,布洛卡点被一个数学爱好者法国军官布洛卡重新发现,并用他的名字命名.问题:已知等腰直角三角形 中,
中, .若
.若 为
为 的布洛卡点,
的布洛卡点, ,则
,则 的值为( )
的值为( )

 内一点
内一点 满足
满足 ,则点
,则点 为
为 的布洛卡点,三角形的布洛卡点由法国数学家和数学教育家克洛尔于1816年首次发现,但他的发现并未被当时的人们所注意.1875年,布洛卡点被一个数学爱好者法国军官布洛卡重新发现,并用他的名字命名.问题:已知等腰直角三角形
的布洛卡点,三角形的布洛卡点由法国数学家和数学教育家克洛尔于1816年首次发现,但他的发现并未被当时的人们所注意.1875年,布洛卡点被一个数学爱好者法国军官布洛卡重新发现,并用他的名字命名.问题:已知等腰直角三角形 中,
中, .若
.若 为
为 的布洛卡点,
的布洛卡点, ,则
,则 的值为( )
的值为( )
| A.10 | B. | C. | D. |
15.化简: _____.
_____.
 _____.
_____.16.如图,边长为3的正方形 中心与半径为3的
中心与半径为3的 的圆心重合,
的圆心重合, ,
, 分别是
分别是 ,
,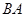 的延长线与
的延长线与 的交点,则图中阴影部分的面积是______(结果保留
的交点,则图中阴影部分的面积是______(结果保留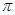 ).
).
 中心与半径为3的
中心与半径为3的 的圆心重合,
的圆心重合, ,
, 分别是
分别是 ,
,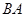 的延长线与
的延长线与 的交点,则图中阴影部分的面积是______(结果保留
的交点,则图中阴影部分的面积是______(结果保留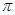 ).
).
17.若正六边形的内切圆半径为3,则其外接圆半径为______.
18.如图,双曲线 经过矩形
经过矩形 的顶点
的顶点 ,双曲线
,双曲线 交
交 ,
, 于点
于点 ,
, 且与矩形的对角线
且与矩形的对角线 交于点
交于点 ,连接
,连接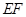 ,若
,若 ,则
,则 的面积为______.
的面积为______.
 经过矩形
经过矩形 的顶点
的顶点 ,双曲线
,双曲线 交
交 ,
, 于点
于点 ,
, 且与矩形的对角线
且与矩形的对角线 交于点
交于点 ,连接
,连接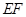 ,若
,若 ,则
,则 的面积为______.
的面积为______.
19.一般的,如果 (
( ,且
,且 ),那么
),那么 叫做以
叫做以 为底
为底 的对数,记作
的对数,记作 .例如:由于
.例如:由于 ,所以3是以2为底8的对数,记作
,所以3是以2为底8的对数,记作 ;由于
;由于 ,所以1是以
,所以1是以 为底
为底 的对数,记作
的对数,记作 .对数作为一种运算,有如下的运算性质如果
.对数作为一种运算,有如下的运算性质如果 ,且
,且 ,
, ,
, ,那么(1)
,那么(1) ;(2)
;(2) ;(3)
;(3) .根据上面的运算性质,计算
.根据上面的运算性质,计算 的结果是_____.
的结果是_____.
 (
( ,且
,且 ),那么
),那么 叫做以
叫做以 为底
为底 的对数,记作
的对数,记作 .例如:由于
.例如:由于 ,所以3是以2为底8的对数,记作
,所以3是以2为底8的对数,记作 ;由于
;由于 ,所以1是以
,所以1是以 为底
为底 的对数,记作
的对数,记作 .对数作为一种运算,有如下的运算性质如果
.对数作为一种运算,有如下的运算性质如果 ,且
,且 ,
, ,
, ,那么(1)
,那么(1) ;(2)
;(2) ;(3)
;(3) .根据上面的运算性质,计算
.根据上面的运算性质,计算 的结果是_____.
的结果是_____.20.计算: .
.
 .
.21.钟南山院士谈到防护新型冠状病毒肺炎时说:“我们需要重视防护,但也不必恐慌,尽量少去人员密集的场所,出门戴口罩,在室内注意通风,勤洗手,多运动,少熬夜.”某学校为了了解学生对新型冠状病毒肺炎防护知识的掌握情况,随机抽取若干名同学利用网络进行了“新冠状病毒肺炎防疫知识”问卷测试.根据测试成绩分布情况,他们将全部测试成绩分成 、
、 、
、 、
、 四组,绘制了如下统计图表:
四组,绘制了如下统计图表:
“新冠状病毒肺炎防疫知识”问卷测试成绩统计表

依据以上统计信息,解答下列问题:
(1)求得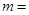 ,
,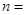 ;
;
(2)这次测试成绩的中位数落在 组;
(3)求本次全部测试成绩的平均数.
 、
、 、
、 、
、 四组,绘制了如下统计图表:
四组,绘制了如下统计图表:“新冠状病毒肺炎防疫知识”问卷测试成绩统计表
| 组别 | 分数/分 | 频数 | 各组总分/分 |
 |  | 38 | 2581 |
 |  |  | 5543 |
 |  | 60 | 5100 |
 |  | 30 | 2796 |

依据以上统计信息,解答下列问题:
(1)求得
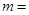 ,
,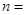 ;
;(2)这次测试成绩的中位数落在 组;
(3)求本次全部测试成绩的平均数.
22.放风筝是大家喜爱的一种运动,星期天的上午小明在市政府广场上放风筝.如图,他在A处不小心让风筝挂在了一棵树梢上,风筝固定在了D处,此时风筝AD与水平线的夹角为30°,为了便于观察,小明迅速向前边移动,收线到达了离A处10米的B处,此时风筝线BD与水平线的夹角为45°.已知点A,B,C在同一条水平直线上,请你求出小明此时所收回的风筝线的长度是多少米?(风筝线AD,BD均为线段,  ≈1.414,
≈1.414,  ≈1.732,最后结果精确到1米).
≈1.732,最后结果精确到1米). 
 ≈1.414,
≈1.414,  ≈1.732,最后结果精确到1米).
≈1.732,最后结果精确到1米). 
23.如图,四边形 内接于⊙O,
内接于⊙O, 为⊙O的直径,
为⊙O的直径, 为的
为的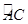 中点,过点
中点,过点 作
作 //
// ,交
,交 的延长线于点
的延长线于点 .
.

(1)判断 与⊙O的位置关系,并说明理由;
与⊙O的位置关系,并说明理由;
(2)若⊙O的半径为6, ,求
,求 的长.
的长.
 内接于⊙O,
内接于⊙O, 为⊙O的直径,
为⊙O的直径, 为的
为的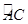 中点,过点
中点,过点 作
作 //
// ,交
,交 的延长线于点
的延长线于点 .
.
(1)判断
 与⊙O的位置关系,并说明理由;
与⊙O的位置关系,并说明理由;(2)若⊙O的半径为6,
 ,求
,求 的长.
的长.24.今年疫情防控期间,我市一家服装有限公司生产了一款服装,为对比分析以前实体商店和现在网上商店两种途径的销售情况,进行了为期30天的跟踪调查.其中实体商店的日销售量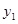 (百件)与时间
(百件)与时间 (
( 为整数,单位:天)的部分对应值如下表所示;网上商店的日销售量
为整数,单位:天)的部分对应值如下表所示;网上商店的日销售量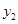 (百件)与时间
(百件)与时间 (
( 为整数,单位:天)的关系如图所示.
为整数,单位:天)的关系如图所示.

(1)请你在一次函数、二次函数和反比例函数中,选择合适的函数反映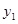 与
与 的变化规律,并求出
的变化规律,并求出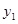 与
与 的函数关系式及自变量
的函数关系式及自变量 的取值范围;
的取值范围;
(2)求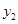 与
与 的函数关系式,并写出自变量
的函数关系式,并写出自变量 的取值范围;
的取值范围;
(3)在跟踪调查的30天中,设实体商店和网上商店的日销售总量为 (百件),求
(百件),求 与
与 的函数关系式;当
的函数关系式;当 为何值时,日销售量
为何值时,日销售量 达到最大,并求出此时的最大值.
达到最大,并求出此时的最大值.
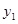 (百件)与时间
(百件)与时间 (
( 为整数,单位:天)的部分对应值如下表所示;网上商店的日销售量
为整数,单位:天)的部分对应值如下表所示;网上商店的日销售量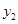 (百件)与时间
(百件)与时间 (
( 为整数,单位:天)的关系如图所示.
为整数,单位:天)的关系如图所示.时间 (天) (天) | 0 | 6 | 10 | 12 | 18 | 20 | 24 | 30 |
日销售量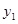 (百件) (百件) | 0 | 72 | 100 | 108 | 108 | 100 | 72 | 0 |

(1)请你在一次函数、二次函数和反比例函数中,选择合适的函数反映
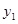 与
与 的变化规律,并求出
的变化规律,并求出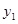 与
与 的函数关系式及自变量
的函数关系式及自变量 的取值范围;
的取值范围;(2)求
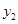 与
与 的函数关系式,并写出自变量
的函数关系式,并写出自变量 的取值范围;
的取值范围;(3)在跟踪调查的30天中,设实体商店和网上商店的日销售总量为
 (百件),求
(百件),求 与
与 的函数关系式;当
的函数关系式;当 为何值时,日销售量
为何值时,日销售量 达到最大,并求出此时的最大值.
达到最大,并求出此时的最大值.25.(1)如图1, 是正方形
是正方形 边
边 上的一点,连接
上的一点,连接 ,
, ,将
,将 绕点
绕点 逆时针旋转
逆时针旋转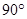 ,旋转后角的两边分别与射线
,旋转后角的两边分别与射线 交于点
交于点 和点
和点 .写出线段
.写出线段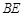 ,
, 和
和 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;



(2)当四边形 为菱形,
为菱形, ,点
,点 是菱形
是菱形 边
边 所在直线上的一点,连接
所在直线上的一点,连接 、
、 ,将
,将 绕点
绕点 逆时针旋转
逆时针旋转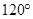 ,旋转后角的两边分别与射线
,旋转后角的两边分别与射线 交于点
交于点 和点
和点 .
.
①如图2,点 在线段
在线段 上时,请探究线段
上时,请探究线段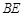 ,
, 和
和 之间的数量关系,写出结论并给出证明;
之间的数量关系,写出结论并给出证明;
②如图3,点 在线段
在线段 的延长线上时,
的延长线上时, 交射线
交射线 于点
于点 ,若
,若 ,
, ,直接写出线段
,直接写出线段 的长度.
的长度.
 是正方形
是正方形 边
边 上的一点,连接
上的一点,连接 ,
, ,将
,将 绕点
绕点 逆时针旋转
逆时针旋转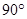 ,旋转后角的两边分别与射线
,旋转后角的两边分别与射线 交于点
交于点 和点
和点 .写出线段
.写出线段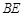 ,
, 和
和 之间的数量关系,并说明理由;
之间的数量关系,并说明理由;


(2)当四边形
 为菱形,
为菱形, ,点
,点 是菱形
是菱形 边
边 所在直线上的一点,连接
所在直线上的一点,连接 、
、 ,将
,将 绕点
绕点 逆时针旋转
逆时针旋转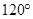 ,旋转后角的两边分别与射线
,旋转后角的两边分别与射线 交于点
交于点 和点
和点 .
.①如图2,点
 在线段
在线段 上时,请探究线段
上时,请探究线段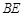 ,
, 和
和 之间的数量关系,写出结论并给出证明;
之间的数量关系,写出结论并给出证明;②如图3,点
 在线段
在线段 的延长线上时,
的延长线上时, 交射线
交射线 于点
于点 ,若
,若 ,
, ,直接写出线段
,直接写出线段 的长度.
的长度.26.如图,在平面直角坐标系xOy中,抛物线L1: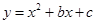 过点C(0,﹣3),与抛物线L2:
过点C(0,﹣3),与抛物线L2: 的一个交点为A,且点A的横坐标为2,点P、Q分别是抛物线L1、抛物线L2上的动点.
的一个交点为A,且点A的横坐标为2,点P、Q分别是抛物线L1、抛物线L2上的动点.
(1)求抛物线L1对应的函数表达式;
(2)若以点A、C、P、Q为顶点的四边形恰为平行四边形,求出点P的坐标;
(3)设点R为抛物线L1上另一个动点,且CA平分∠PCR,若OQ∥PR,求出点Q的坐标.

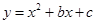 过点C(0,﹣3),与抛物线L2:
过点C(0,﹣3),与抛物线L2: 的一个交点为A,且点A的横坐标为2,点P、Q分别是抛物线L1、抛物线L2上的动点.
的一个交点为A,且点A的横坐标为2,点P、Q分别是抛物线L1、抛物线L2上的动点.(1)求抛物线L1对应的函数表达式;
(2)若以点A、C、P、Q为顶点的四边形恰为平行四边形,求出点P的坐标;
(3)设点R为抛物线L1上另一个动点,且CA平分∠PCR,若OQ∥PR,求出点Q的坐标.

 搜索
搜索
 难度系数:0.85
难度系数:0.85  答案解析
答案解析
 有奖纠错
有奖纠错
