搜索
全一卷
难度系数：0.85 
答案解析
有奖纠错
1．﹣
的绝对值为（ ）
的绝对值为（ ）| A．﹣2 | B．﹣ | C． | D．1 |
2．目前我国能制造芯片的最小工艺水平是16纳米，已知1纳米＝10－9米，用科学记数法将16纳米表示为（ ）
| A．1.6×10－9米 | B．1.6×10－8米 | C．1.6×10－7米 | D．16×10－9米 |
3．如图是由6个大小相同的小正方体组成的几何体，它的主视图是（ ）
A． | B． | C． | D． |
4．下列计算正确的是（ ）
A． | B． | C． | D． |
5．下列二次根式中属于最简二次根式的是( )
A． | B． | C． | D． |
6．如图，AB∥CD，以点A为圆心，小于AC长为半径作圆弧，分别交AB，AC于E，F两点，再分别以E，F为圆心，大于
EF长为半径作圆弧，两条圆弧交于点P，连接AP，交CD于点M，若∠ACD＝110°，则∠CMA的度数为（ ）
EF长为半径作圆弧，两条圆弧交于点P，连接AP，交CD于点M，若∠ACD＝110°，则∠CMA的度数为（ ）| A．30° | B．35° | C．70° | D．45° |
7．关于x的一元一次不等式
≤﹣2的解集为x≥4，则m的值为（ ）
≤﹣2的解集为x≥4，则m的值为（ ）| A．14 | B．7 | C．﹣2 | D．2 |
8．如图，已知⊙O上三点A，B，C，半径OC=1，∠ABC=30°，切线PA交OC延长线于点P，则PA的长为（ ）
| A．2 | B． | C． | D． |
9．如图，由四个直角边分别是6和8的全等直角三角形拼成的“赵爽弦图”，随机往大正方形区域内投针一次，则针扎在小正方形GHEF部分的概率是（ ）
A． | B． | C． | D． |
10．如图，正方形
的边长为4，点
是
的中点，点
从点出发，沿
移动至终点
，设点经过的路径长为
，
的面积为
，则下列图象能大致反映与函数关系的是（ ）
的边长为4，点是的中点，点从点出发，沿移动至终点，设点经过的路径长为，的面积为，则下列图象能大致反映与函数关系的是（ ）A． | B． | C． | D． |
11．分解因式：x3y﹣2x2y+xy=______ ．
12．若关于x的分式方程
有增根，则m的值为_______ ．
有增根，则m的值为13．在平面直角坐标系中，Rt△OAB的顶点A的坐标为（
，1），若将△OAB绕O点，逆时针旋转60°后，B点到达B′点，则点B′的坐标是_______ ．
，1），若将△OAB绕O点，逆时针旋转60°后，B点到达B′点，则点B′的坐标是14．如图，将矩形ABCD绕点A旋转至矩形AEFG的位置，此时点D恰好与AF的中点重合，AE交CD于点H，若BC＝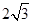
，则HC的长为________ ．
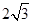，则HC的长为________ ．
15．如图，在平面直角坐标系中，
，
，
，．．．都是等腰直角三角形，其直角顶点
，
，
，．．．均在直线
上，设，，，．．．的面积分别为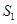
，
，
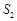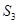，．．．，依据图形所反映的规律，S2020＝__________．
，
，
，．．．都是等腰直角三角形，其直角顶点
，
，
，．．．均在直线
上，设，，，．．．的面积分别为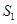
，
，
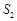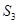，．．．，依据图形所反映的规律，S2020＝__________．
16．先化简，再求值：
，其中
.
，其中.17．某市明年的初中毕业升学考试，拟将“引体向上”作为男生体育考试的一个必考项目，满分为10分．有关部门为提前了解明年参加初中毕业升学考试的男生的“引体向上”水平，在全市八年级男生中随机抽取了部分男生，对他们的“引体向上”水平进行测试，并将测试结果绘制成如下统计图表（部分信息未给出）：
请你根据统计图表中的信息，解答下列问题：
抽取的男生“引体向上”成绩统计表
（1）填空：m＝ ，n＝ ．
（2）求扇形统计图中D组的扇形圆心角的度数；
（3）目前该市八年级有男生3600名，请估计其中“引体向上”得零分的人数．
请你根据统计图表中的信息，解答下列问题：
抽取的男生“引体向上”成绩统计表
| 成绩 | 人数 |
| 0分 | 32 |
| 1分 | 30 |
| 2分 | 24 |
| 3分 | 11 |
| 4分 | 15 |
| 5分及以上 | m |
（1）填空：m＝ ，n＝ ．
（2）求扇形统计图中D组的扇形圆心角的度数；
（3）目前该市八年级有男生3600名，请估计其中“引体向上”得零分的人数．
18．如图，在足够大的空地上有一段长为a（a≥50）米的旧墙MN，某人利用旧墙和木栏围成一个矩形菜园ABCD，其中AD≤MN，已知矩形菜园的一边靠墙，另三边一共用了100米木栏．
（1）若围成的矩形菜园的面积为450平方米，求所利用旧墙AD的长；
（2）求矩形菜园ABCD面积的最大值．
（1）若围成的矩形菜园的面积为450平方米，求所利用旧墙AD的长；
（2）求矩形菜园ABCD面积的最大值．
19．如图，在平面直角坐标系
中，一次函数
的图像与反比例函数
的图像在第二象限交于点
，与
轴交于点
，点
在
轴上，满足条件：
，且
，点的坐标为
，
。
（1）求反比例函数的表达式；
（2）直接写出当
时，
的解集。
中，一次函数
的图像与反比例函数
的图像在第二象限交于点
，与
轴交于点
，点
在
轴上，满足条件：
，且
，点的坐标为
，
。
（1）求反比例函数的表达式；
（2）直接写出当
时，
的解集。20．在平面直角坐标系中，⊙M过坐标原点O且分别交x轴、y轴于点A，B，点C为第一象限内⊙M上一点．若点A（6，0），∠BCO＝30°．
（1）求点B的坐标；
（2）若点D的坐标为（-2，0），试猜想直线DB与⊙M的位置关系，并说明理由．
（1）求点B的坐标；
（2）若点D的坐标为（-2，0），试猜想直线DB与⊙M的位置关系，并说明理由．
21．（1）某学校“智慧方园”数学社团遇到这样一个题目：
如图1，在△ABC中，点O在线段BC上，∠BAO=30°，∠OAC=75°，AO=
，BO：CO=1：3，求AB的长．
经过社团成员讨论发现，过点B作BD∥AC，交AO的延长线于点D，通过构造△ABD就可以解决问题（如图2）．
请回答：∠ADB= °，AB= ．
（2）请参考以上解决思路，解决问题：
如图3，在四边形ABCD中，对角线AC与BD相交于点O，AC⊥AD，AO=，∠ABC=∠ACB=75°，BO：OD=1：3，求DC的长．
如图1，在△ABC中，点O在线段BC上，∠BAO=30°，∠OAC=75°，AO=
，BO：CO=1：3，求AB的长．经过社团成员讨论发现，过点B作BD∥AC，交AO的延长线于点D，通过构造△ABD就可以解决问题（如图2）．
请回答：∠ADB= °，AB= ．
（2）请参考以上解决思路，解决问题：
如图3，在四边形ABCD中，对角线AC与BD相交于点O，AC⊥AD，AO=
，∠ABC=∠ACB=75°，BO：OD=1：3，求DC的长．
22．如图，抛物线y=ax2﹣5ax+c与坐标轴分别交于点A，C，E三点，其中A（﹣3，0），C（0，4），点B在x轴上，AC=BC，过点B作BD⊥x轴交抛物线于点D，点M，N分别是线段CO，BC上的动点，且CM=BN，连接MN，AM，AN．
（1）求抛物线的解析式及点D的坐标；
（2）当△CMN是直角三角形时，求点M的坐标；
（3）试求出AM+AN的最小值．
（1）求抛物线的解析式及点D的坐标；
（2）当△CMN是直角三角形时，求点M的坐标；
（3）试求出AM+AN的最小值．
