全一卷
1.如图,在平面内作已知直线 的垂线,可作垂线的条数有( )
的垂线,可作垂线的条数有( )

 的垂线,可作垂线的条数有( )
的垂线,可作垂线的条数有( )
| A.0条 | B.1条 | C.2条 | D.无数条 |
2.墨迹覆盖了等式“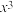
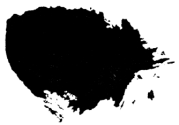
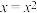 (
(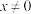 )”中的运算符号,则覆盖的是( )
)”中的运算符号,则覆盖的是( )
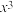

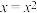 (
(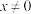 )”中的运算符号,则覆盖的是( )
)”中的运算符号,则覆盖的是( ) | A.+ | B.- | C.× | D.÷ |
3.对于① ,②
,② ,从左到右的变形,表述正确的是( )
,从左到右的变形,表述正确的是( )
 ,②
,② ,从左到右的变形,表述正确的是( )
,从左到右的变形,表述正确的是( )| A.都是因式分解 | B.都是乘法运算 |
| C.①是因式分解,②是乘法运算 | D.①是乘法运算,②是因式分解 |
4.如图的两个几何体分别由7个和6个相同的小正方体搭成,比较两个几何体的三视图,正确的是( )


| A.仅主视图不同 | B.仅俯视图不同 |
| C.仅左视图不同 | D.主视图、左视图和俯视图都相同 |
5.如图是小颖前三次购买苹果单价的统计图,第四次又买的苹果单价是 元/千克,发现这四个单价的中位数恰好也是众数,则
元/千克,发现这四个单价的中位数恰好也是众数,则 ( )
( )

 元/千克,发现这四个单价的中位数恰好也是众数,则
元/千克,发现这四个单价的中位数恰好也是众数,则 ( )
( )
| A.9 | B.8 | C.7 | D.6 |
6.如图1,已知 ,用尺规作它的角平分线.
,用尺规作它的角平分线.
如图2,步骤如下,
第一步:以 为圆心,以
为圆心,以 为半径画弧,分别交射线
为半径画弧,分别交射线 ,
, 于点
于点 ,
, ;
;
第二步:分别以 ,
, 为圆心,以
为圆心,以 为半径画弧,两弧在
为半径画弧,两弧在 内部交于点
内部交于点 ;
;
第三步:画射线 .射线
.射线 即为所求.
即为所求.
下列正确的是( )

 ,用尺规作它的角平分线.
,用尺规作它的角平分线.如图2,步骤如下,
第一步:以
 为圆心,以
为圆心,以 为半径画弧,分别交射线
为半径画弧,分别交射线 ,
, 于点
于点 ,
, ;
;第二步:分别以
 ,
, 为圆心,以
为圆心,以 为半径画弧,两弧在
为半径画弧,两弧在 内部交于点
内部交于点 ;
;第三步:画射线
 .射线
.射线 即为所求.
即为所求.下列正确的是( )

A. , , 均无限制 均无限制 | B. , , 的长 的长 |
C. 有最小限制, 有最小限制, 无限制 无限制 | D. , , 的长 的长 |
7.若 ,则下列分式化简正确的是( )
,则下列分式化简正确的是( )
 ,则下列分式化简正确的是( )
,则下列分式化简正确的是( )A. | B. | C. | D. |
8.在如图所示的网格中,以点 为位似中心,四边形
为位似中心,四边形 的位似图形是( )
的位似图形是( )

 为位似中心,四边形
为位似中心,四边形 的位似图形是( )
的位似图形是( )
A.四边形 | B.四边形 | C.四边形 | D.四边形 |
9.若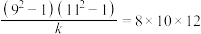 ,则
,则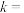 ( )
( )
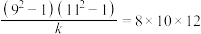 ,则
,则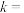 ( )
( )| A.12 | B.10 | C.8 | D.6 |
10.如图,将 绕边
绕边 的中点
的中点 顺时针旋转180°.嘉淇发现,旋转后的
顺时针旋转180°.嘉淇发现,旋转后的 与
与 构成平行四边形,并推理如下:
构成平行四边形,并推理如下:

小明为保证嘉淇的推理更严谨,想在方框中“∵ ,”和“∴四边形……”之间作补充.下列正确的是( )
,”和“∴四边形……”之间作补充.下列正确的是( )
 绕边
绕边 的中点
的中点 顺时针旋转180°.嘉淇发现,旋转后的
顺时针旋转180°.嘉淇发现,旋转后的 与
与 构成平行四边形,并推理如下:
构成平行四边形,并推理如下:点 , , 分别转到了点 分别转到了点 , , 处, 处,而点  转到了点 转到了点 处. 处.∵  , ,∴四边形  是平行四边形. 是平行四边形. |

小明为保证嘉淇的推理更严谨,想在方框中“∵
 ,”和“∴四边形……”之间作补充.下列正确的是( )
,”和“∴四边形……”之间作补充.下列正确的是( )| A.嘉淇推理严谨,不必补充 | B.应补充:且 , , |
C.应补充:且 | D.应补充:且 , , |
11.若 为正整数,则
为正整数,则 ( )
( )
 为正整数,则
为正整数,则 ( )
( )A. | B. | C. | D. |
12.如图,从笔直的公路 旁一点
旁一点 出发,向西走
出发,向西走 到达
到达 ;从
;从 出发向北走
出发向北走 也到达
也到达 .下列说法
.下列说法错误 的是( )

 旁一点
旁一点 出发,向西走
出发,向西走 到达
到达 ;从
;从 出发向北走
出发向北走 也到达
也到达 .下列说法
.下列说法
A.从点 向北偏西45°走 向北偏西45°走 到达 到达 |
B.公路 的走向是南偏西45° 的走向是南偏西45° |
C.公路 的走向是北偏东45° 的走向是北偏东45° |
D.从点 向北走 向北走 后,再向西走 后,再向西走 到达 到达 |
13.已知光速为300000千米秒,光经过 秒(
秒( )传播的距离用科学记数法表示为
)传播的距离用科学记数法表示为 千米,则
千米,则 可能为( )
可能为( )
 秒(
秒( )传播的距离用科学记数法表示为
)传播的距离用科学记数法表示为 千米,则
千米,则 可能为( )
可能为( )| A.5 | B.6 | C.5或6 | D.5或6或7 |
14.有一题目:“已知;点 为
为 的外心,
的外心, ,求
,求 .”嘉嘉的解答为:画
.”嘉嘉的解答为:画 以及它的外接圆
以及它的外接圆 ,连接
,连接 ,
, ,如图.由
,如图.由 ,得
,得 .而淇淇说:“嘉嘉考虑的不周全,
.而淇淇说:“嘉嘉考虑的不周全, 还应有另一个不同的值.”,下列判断正确的是( )
还应有另一个不同的值.”,下列判断正确的是( )

 为
为 的外心,
的外心, ,求
,求 .”嘉嘉的解答为:画
.”嘉嘉的解答为:画 以及它的外接圆
以及它的外接圆 ,连接
,连接 ,
, ,如图.由
,如图.由 ,得
,得 .而淇淇说:“嘉嘉考虑的不周全,
.而淇淇说:“嘉嘉考虑的不周全, 还应有另一个不同的值.”,下列判断正确的是( )
还应有另一个不同的值.”,下列判断正确的是( )
A.淇淇说的对,且 的另一个值是115° 的另一个值是115° |
B.淇淇说的不对, 就得65° 就得65° |
C.嘉嘉求的结果不对, 应得50° 应得50° |
D.两人都不对, 应有3个不同值 应有3个不同值 |
15.如图,现要在抛物线 上找点
上找点 ,针对
,针对 的不同取值,所找点
的不同取值,所找点 的个数,三人的说法如下,
的个数,三人的说法如下,
甲:若 ,则点
,则点 的个数为0;
的个数为0;
乙:若 ,则点
,则点 的个数为1;
的个数为1;
丙:若 ,则点
,则点 的个数为1.
的个数为1.
下列判断正确的是( )

 上找点
上找点 ,针对
,针对 的不同取值,所找点
的不同取值,所找点 的个数,三人的说法如下,
的个数,三人的说法如下,甲:若
 ,则点
,则点 的个数为0;
的个数为0;乙:若
 ,则点
,则点 的个数为1;
的个数为1;丙:若
 ,则点
,则点 的个数为1.
的个数为1.下列判断正确的是( )

| A.乙错,丙对 | B.甲和乙都错 |
| C.乙对,丙错 | D.甲错,丙对 |
16.如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是1,2,3,4,5,选取其中三块(可重复选取)按图的方式组成图案,使所围成的三角形是面积最大 的直角三角形,则选取的三块纸片的面积分别是( )


| A.1,4,5 | B.2,3,5 | C.3,4,5 | D.2,2,4 |
17.已知: ,则
,则
_________ .
 ,则
,则
18.正六边形的一个内角是正 边形一个外角的4倍,则
边形一个外角的4倍,则
_________ .
 边形一个外角的4倍,则
边形一个外角的4倍,则
19.如图是8个台阶的示意图,每个台阶的高和宽分别是1和2,每个台阶凸出的角的顶点记作 (
( 为1~8的整数).函数
为1~8的整数).函数 (
( )的图象为曲线
)的图象为曲线 .
.

(1)若 过点
过点 ,则
,则
_________ ;
(2)若 过点
过点 ,则它必定还过另一点
,则它必定还过另一点 ,则
,则
_________ ;
(3)若曲线 使得
使得 这些点分布在它的两侧,每侧各4个点,则
这些点分布在它的两侧,每侧各4个点,则 的整数值有
的整数值有_________ 个.
 (
( 为1~8的整数).函数
为1~8的整数).函数 (
( )的图象为曲线
)的图象为曲线 .
.
(1)若
 过点
过点 ,则
,则
(2)若
 过点
过点 ,则它必定还过另一点
,则它必定还过另一点 ,则
,则
(3)若曲线
 使得
使得 这些点分布在它的两侧,每侧各4个点,则
这些点分布在它的两侧,每侧各4个点,则 的整数值有
的整数值有20.已知两个有理数:-9和5.
(1)计算: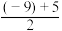 ;
;
(2)若再添一个负整数 ,且-9,5与
,且-9,5与 这三个数的平均数仍小于
这三个数的平均数仍小于 ,求
,求 的值.
的值.
(1)计算:
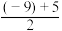 ;
;(2)若再添一个负整数
 ,且-9,5与
,且-9,5与 这三个数的平均数仍小于
这三个数的平均数仍小于 ,求
,求 的值.
的值.21.有一电脑程序:每按一次按键,屏幕的 区就会自动加上
区就会自动加上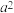 ,同时
,同时 区就会自动减去
区就会自动减去 ,且均显示化简后的结果.已知
,且均显示化简后的结果.已知 ,
, 两区初始显示的分别是25和-16,如图.
两区初始显示的分别是25和-16,如图.
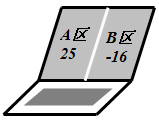
如,第一次按键后, ,
, 两区分别显示:
两区分别显示:
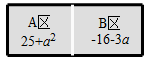
(1)从初始状态按2次后,分别求 ,
, 两区显示的结果;
两区显示的结果;
(2)从初始状态按4次后,计算 ,
, 两区代数式的和,请判断这个和能为负数吗?说明理由.
两区代数式的和,请判断这个和能为负数吗?说明理由.
 区就会自动加上
区就会自动加上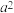 ,同时
,同时 区就会自动减去
区就会自动减去 ,且均显示化简后的结果.已知
,且均显示化简后的结果.已知 ,
, 两区初始显示的分别是25和-16,如图.
两区初始显示的分别是25和-16,如图.
如,第一次按键后,
 ,
, 两区分别显示:
两区分别显示: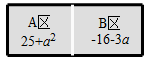
(1)从初始状态按2次后,分别求
 ,
, 两区显示的结果;
两区显示的结果;(2)从初始状态按4次后,计算
 ,
, 两区代数式的和,请判断这个和能为负数吗?说明理由.
两区代数式的和,请判断这个和能为负数吗?说明理由.22.如图,点 为
为 中点,分别延长
中点,分别延长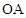 到点
到点 ,
, 到点
到点 ,使
,使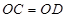 .以点
.以点 为圆心,分别以
为圆心,分别以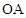 ,
, 为半径在
为半径在 上方作两个半圆.点
上方作两个半圆.点 为小半圆上任一点(不与点
为小半圆上任一点(不与点 ,
, 重合),连接
重合),连接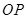 并延长交大半圆于点
并延长交大半圆于点 ,连接
,连接 ,
, .
.


(1)①求证: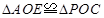 ;
;
②写出∠1,∠2和 三者间的数量关系,并说明理由.
三者间的数量关系,并说明理由.
(2)若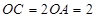 ,当
,当 最大时,直接指出
最大时,直接指出 与小半圆的位置关系,并求此时
与小半圆的位置关系,并求此时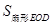 (答案保留
(答案保留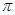 ).
).
 为
为 中点,分别延长
中点,分别延长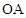 到点
到点 ,
, 到点
到点 ,使
,使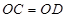 .以点
.以点 为圆心,分别以
为圆心,分别以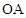 ,
, 为半径在
为半径在 上方作两个半圆.点
上方作两个半圆.点 为小半圆上任一点(不与点
为小半圆上任一点(不与点 ,
, 重合),连接
重合),连接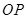 并延长交大半圆于点
并延长交大半圆于点 ,连接
,连接 ,
, .
.

(1)①求证:
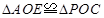 ;
;②写出∠1,∠2和
 三者间的数量关系,并说明理由.
三者间的数量关系,并说明理由.(2)若
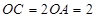 ,当
,当 最大时,直接指出
最大时,直接指出 与小半圆的位置关系,并求此时
与小半圆的位置关系,并求此时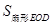 (答案保留
(答案保留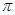 ).
).23.用承重指数 衡量水平放置的长方体木板的最大承重量.实验室有一些同材质同长同宽而厚度不一的木板,实验发现:木板承重指数
衡量水平放置的长方体木板的最大承重量.实验室有一些同材质同长同宽而厚度不一的木板,实验发现:木板承重指数 与木板厚度
与木板厚度 (厘米)的平方成正比,当
(厘米)的平方成正比,当 时,
时, .
.
(1)求 与
与 的函数关系式.
的函数关系式.
(2)如图,选一块厚度为6厘米的木板,把它分割成与原来同长同宽但薄厚不同的两块板(不计分割损耗).设薄板的厚度为 (厘米),
(厘米), .
.

①求 与
与 的函数关系式;
的函数关系式;
② 为何值时,
为何值时, 是
是 的3倍?
的3倍?
【注:(1)及(2)中的①不必写 的取值范围】
的取值范围】
 衡量水平放置的长方体木板的最大承重量.实验室有一些同材质同长同宽而厚度不一的木板,实验发现:木板承重指数
衡量水平放置的长方体木板的最大承重量.实验室有一些同材质同长同宽而厚度不一的木板,实验发现:木板承重指数 与木板厚度
与木板厚度 (厘米)的平方成正比,当
(厘米)的平方成正比,当 时,
时, .
.(1)求
 与
与 的函数关系式.
的函数关系式.(2)如图,选一块厚度为6厘米的木板,把它分割成与原来同长同宽但薄厚不同的两块板(不计分割损耗).设薄板的厚度为
 (厘米),
(厘米), .
.
①求
 与
与 的函数关系式;
的函数关系式;②
 为何值时,
为何值时, 是
是 的3倍?
的3倍?【注:(1)及(2)中的①不必写
 的取值范围】
的取值范围】24.表格中的两组对应值满足一次函数 ,现画出了它的图象为直线
,现画出了它的图象为直线 ,如图.而某同学为观察
,如图.而某同学为观察 ,
, 对图象的影响,将上面函数中的
对图象的影响,将上面函数中的 与
与 交换位置后得另一个一次函数,设其图象为直线
交换位置后得另一个一次函数,设其图象为直线 .
.

(1)求直线 的解析式;
的解析式;
(2)请在图上画出 直线 (不要求列表计算),并求直线
(不要求列表计算),并求直线 被直线
被直线 和
和 轴所截线段的长;
轴所截线段的长;
(3)设直线 与直线
与直线 ,
, 及
及 轴有三个不同的交点,且其中两点关于第三点对称,
轴有三个不同的交点,且其中两点关于第三点对称,直接 写出 的值.
的值.
 ,现画出了它的图象为直线
,现画出了它的图象为直线 ,如图.而某同学为观察
,如图.而某同学为观察 ,
, 对图象的影响,将上面函数中的
对图象的影响,将上面函数中的 与
与 交换位置后得另一个一次函数,设其图象为直线
交换位置后得另一个一次函数,设其图象为直线 .
. | -1 | 0 |
 | -2 | 1 |

(1)求直线
 的解析式;
的解析式;(2)请在图上
 (不要求列表计算),并求直线
(不要求列表计算),并求直线 被直线
被直线 和
和 轴所截线段的长;
轴所截线段的长;(3)设直线
 与直线
与直线 ,
, 及
及 轴有三个不同的交点,且其中两点关于第三点对称,
轴有三个不同的交点,且其中两点关于第三点对称, 的值.
的值.25.如图,甲、乙两人(看成点)分别在数轴-3和5的位置上,沿数轴做移动游戏.每次移动游戏规则:裁判先捂住一枚硬币,再让两人猜向上一面是正是反,而后根据所猜结果进行移动.
①若都对或都错,则甲向东移动1个单位,同时乙向西移动1个单位;
②若甲对乙错,则甲向东移动4个单位,同时乙向东移动2个单位;
③若甲错乙对,则甲向西移动2个单位,同时乙向西移动4个单位.

(1)经过第一次移动游戏,求甲的位置停留在正半轴上的概率 ;
;
(2)从图的位置开始,若完成了10次移动游戏,发现甲、乙每次所猜结果均为一对一错.设乙猜对 次,且他最终停留的位置对应的数为
次,且他最终停留的位置对应的数为 ,试用含
,试用含 的代数式表示
的代数式表示 ,并求该位置距离原点
,并求该位置距离原点 最近时
最近时 的值;
的值;
(3)从图的位置开始,若进行了 次移动游戏后,甲与乙的位置相距2个单位,直接写出
次移动游戏后,甲与乙的位置相距2个单位,直接写出 的值.
的值.
①若都对或都错,则甲向东移动1个单位,同时乙向西移动1个单位;
②若甲对乙错,则甲向东移动4个单位,同时乙向东移动2个单位;
③若甲错乙对,则甲向西移动2个单位,同时乙向西移动4个单位.

(1)经过第一次移动游戏,求甲的位置停留在正半轴上的概率
 ;
;(2)从图的位置开始,若完成了10次移动游戏,发现甲、乙每次所猜结果均为一对一错.设乙猜对
 次,且他最终停留的位置对应的数为
次,且他最终停留的位置对应的数为 ,试用含
,试用含 的代数式表示
的代数式表示 ,并求该位置距离原点
,并求该位置距离原点 最近时
最近时 的值;
的值;(3)从图的位置开始,若进行了
 次移动游戏后,甲与乙的位置相距2个单位,直接写出
次移动游戏后,甲与乙的位置相距2个单位,直接写出 的值.
的值.26.如图1和图2,在 中,
中, ,
, ,
, .点
.点 在
在 边上,点
边上,点 ,
, 分别在
分别在 ,
, 上,且
上,且 .点
.点 从点
从点 出发沿折线
出发沿折线 匀速移动,到达点
匀速移动,到达点 时停止;而点
时停止;而点 在
在 边上随
边上随 移动,且始终保持
移动,且始终保持 .
.

(1)当点 在
在 上时,求点
上时,求点 与点
与点 的最短距离;
的最短距离;
(2)若点 在
在 上,且
上,且 将
将 的面积分成上下4:5两部分时,求
的面积分成上下4:5两部分时,求 的长;
的长;
(3)设点 移动的路程为
移动的路程为 ,当
,当 及
及 时,分别求点
时,分别求点 到直线
到直线 的距离(用含
的距离(用含 的式子表示);
的式子表示);
(4)在点 处设计并安装一扫描器,按定角
处设计并安装一扫描器,按定角 扫描
扫描 区域(含边界),扫描器随点
区域(含边界),扫描器随点 从
从 到
到 再到
再到 共用时36秒.若
共用时36秒.若 ,请
,请直接 写出点 被扫描到的总时长.
被扫描到的总时长.
 中,
中, ,
, ,
, .点
.点 在
在 边上,点
边上,点 ,
, 分别在
分别在 ,
, 上,且
上,且 .点
.点 从点
从点 出发沿折线
出发沿折线 匀速移动,到达点
匀速移动,到达点 时停止;而点
时停止;而点 在
在 边上随
边上随 移动,且始终保持
移动,且始终保持 .
.
(1)当点
 在
在 上时,求点
上时,求点 与点
与点 的最短距离;
的最短距离;(2)若点
 在
在 上,且
上,且 将
将 的面积分成上下4:5两部分时,求
的面积分成上下4:5两部分时,求 的长;
的长;(3)设点
 移动的路程为
移动的路程为 ,当
,当 及
及 时,分别求点
时,分别求点 到直线
到直线 的距离(用含
的距离(用含 的式子表示);
的式子表示);(4)在点
 处设计并安装一扫描器,按定角
处设计并安装一扫描器,按定角 扫描
扫描 区域(含边界),扫描器随点
区域(含边界),扫描器随点 从
从 到
到 再到
再到 共用时36秒.若
共用时36秒.若 ,请
,请 被扫描到的总时长.
被扫描到的总时长. 搜索
搜索
 难度系数:0.85
难度系数:0.85  答案解析
答案解析
 有奖纠错
有奖纠错
