搜索
全一卷
难度系数：0.94 
答案解析
有奖纠错
1．﹣3的相反数是（ ）
A． | B． | C． | D． |
2．下列运算正确的是( )
A． | B． | C． | D． |
3．2014年连云港高票当选全国“十大幸福城市”，在江苏十三个省辖市中居第一位，居民人均可支配收入约18 000元．其中“18 000”用科学记数法表示为
A． | B． | C． | D． |
4．某校要从四名学生中选拔一名参加市“风华小主播”大赛，选拔赛中每名学生的平均成绩
及其方差
如表所示．如果要选择一名成绩高且发挥稳定的学生参赛，则应选择的学生是（ ）
及其方差
如表所示．如果要选择一名成绩高且发挥稳定的学生参赛，则应选择的学生是（ ）| 甲 | 乙 | 丙 | 丁 | |
| 8 | 9 | 9 | 8 |
| 1 | 1 | 1.2 | 1.3 |
| A．甲 | B．乙 | C．丙 | D．丁 |
5．已知四边形ABCD，下列说法正确的是（ ）
| A．当AD=BC，AB//DC时，四边形ABCD是平行四边形 |
| B．当AD=BC，AB＝DC时，四边形ABCD是平行四边形 |
| C．当AC=BD，AC平分BD时，四边形ABCD是矩形 |
| D．当AC=BD，AC⊥BD时，四边形ABCD是正方形 |
6．已知关于x的方程x2﹣2x+3k=0有两个不相等的实数根，则k的取值范围是（ ）
A．k＜ | B．k＞- | C．k＜且k≠0 | D．k＞-且k≠0 |
7．如图，O为坐标原点，菱形OABC的顶点A的坐标为
，顶点C在
轴的负半轴上，函数
的图象经过顶点B，则
的值为（ ）
，顶点C在轴的负半轴上，函数的图象经过顶点B，则的值为（ ）A． | B． | C． | D． |
8．如图是本地区一种产品30天的销售图象，产品日销售量y（单位：件）与时间t（单位：天）的大致函数关系如图①，图②是一件产品的销售利润z（单位：元）与时间t（单位：天）的函数关系，已知日销售利润=日销售量×一件产品的销售利润，下列结论错误 的是（ ）
| A．日销售量为150件的是第12天与第30天 |
| B．第10天销售一件产品的利润是15元 |
| C．从第1天到第20天这段时间内日销售利润将先增加再减少 |
| D．第18天的日销售利润是1225元 |
9．数轴上表示－2的点与原点的距离是_________ ．
10．代数式
在实数范围内有意义，则
的取值范围是_______ ．
在实数范围内有意义，则
的取值范围是11．已知m+n=mn,则(m-1)(n-1)=_______ .
12．如图，一个零件的横截面是六边形，这个六边形的内角和为______ 
．
．
13．已知一个函数，当
时，函数值
随着的增大而减小，请写出这个函数关系式________ （写出一个即可）．
时，函数值
随着的增大而减小，请写出这个函数关系式14．如图是一个几何体的三视图，其中主视图与左视图都是边长为4的等边三角形，则这个几何体的侧面展开图的面积为___ .
15．在△ABC中，AB=4，AC=3，AD是△ABC的角平分线，则△ABD与△ACD的面积之比是_____ ．
16．如图，在△ABC中，
，
，直线
//
//
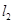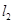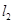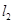，与之间距离是1，与之间距离是2．且，，分别经过点A， B，C，则边AC的长为_____ ．
，
，直线
//
//
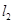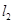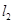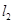，与之间距离是1，与之间距离是2．且，，分别经过点A， B，C，则边AC的长为
17．计算：
．
．18．化简：
．
．19．解不等式组
20．随着我市社会经济的发展和交通状况的改善，我市的旅游业得到了高速发展，某旅游公司对我市一企业个人旅游年消费情况进行问卷调查，随机抽查部分员工，记录每个人年消费金额，并将调查数据适当整理，绘制成尚不完整的表和图(如图)．
| 组别 | 个人年消费金额x/元 | 频数(人数) | 频率 |
| A | x≤2 000 | 18 | 0.15 |
| B | 2 000＜x≤4 000 | a | b |
| C | 4 000＜x≤6 000 | | |
| D | 6 000＜x≤8 000 | 24 | 0.20 |
| E | x＞8 000 | 12 | 0.10 |
| | 合计 | c | 1.00 |
根据以上信息回答下列问题：
(1)a＝________，b＝________，c＝________，并将条形统计图补充完整；
(2)在这次调查中，个人年消费金额的中位数出现在________组；
(3)若这个企业有3 000名员工，请你估计个人旅游年消费金额在6 000元以上的人数．
21．九（1）班组织班级联欢会，最后进入抽奖环节，每名同学都有一次抽奖机会，抽奖方案如下：将一副扑克牌中点数为“2”，“3”，“3”，“5”，“6”的五张牌背面朝上洗匀，先从中抽出1张牌，再从余下的4张牌中抽出1张牌，记录两张牌点数后放回，完成一次抽奖，记每次抽出两张牌点数之差为
，按表格要求确定奖项．
（1）用列表或画树状图的方法求出甲同学获得一等奖的概率；
（2）是否每次抽奖都会获奖，为什么？
，按表格要求确定奖项．
（1）用列表或画树状图的方法求出甲同学获得一等奖的概率；
（2）是否每次抽奖都会获奖，为什么？
22．如图，将平行四边形ABCD沿对角线BD进行折叠，折叠后点C落在点F处，DF交AB于点E．
（1）求证：
；
（2）判断AF与BD是否平行，并说明理由．
（1）求证：
；（2）判断AF与BD是否平行，并说明理由．
23．在某市组织的大型商业演出活动中，对团体购买门票实行优惠，决定在原定票价基础上每张降价80元，这样按原定票价需花费6000元购买的门票张数，现在只花费了4800元．
（1）求每张门票原定的票价；
（2）根据实际情况，活动组织单位决定对于个人购票也采取优惠措施，原定票价经过连续二次降价后降为324元，求平均每次降价的百分率．
（1）求每张门票原定的票价；
（2）根据实际情况，活动组织单位决定对于个人购票也采取优惠措施，原定票价经过连续二次降价后降为324元，求平均每次降价的百分率．
24．（本题满分10分）已知如图，在平面直角坐标系
中，直线
与
轴、
轴分别交于A，B两点，P是直线AB上一动点，⊙
的半径为1．
（1）判断原点O与⊙的位置关系，并说明理由；
（2）当⊙过点B时，求⊙被轴所截得的劣弧的长；
（3）当⊙与轴相切时，求出切点的坐标．
中，直线
与
轴、
轴分别交于A，B两点，P是直线AB上一动点，⊙
的半径为1．
（1）判断原点O与⊙
的位置关系，并说明理由；（2）当⊙
过点B时，求⊙被轴所截得的劣弧的长；（3）当⊙
与轴相切时，求出切点的坐标．25．如图，在△ABC中，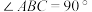
，
，D为AC延长线上一点，
．过点D作
//
，交
的延长线于点H．
（1）求
的值；
（2）若
，求AB的长．
，
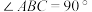，D为AC延长线上一点，
．过点D作
//
，交
的延长线于点H．
（1）求
的值；（2）若
，求AB的长．26．在数学兴趣小组活动中，小明进行数学探究活动．将边长为2的正方形ABCD与边长为
的正方形AEFG按图1位置放置，AD与AE在同一条直线上，AB与AG在同一条直线上．
（1）小明发现
，请你帮他说明理由．
（2）如图2，小明将正方形ABCD绕点A逆时针旋转，当点B恰好落在线段DG上时，请你帮他求出此时BE的长．
（3）如图3，若小明将正方形ABCD绕点A继续逆时针旋转，线段DG与线段BE将相交，交点为H，写出△
与△面积之和的最大值，并简要说明理由．
的正方形AEFG按图1位置放置，AD与AE在同一条直线上，AB与AG在同一条直线上．（1）小明发现
，请你帮他说明理由．（2）如图2，小明将正方形ABCD绕点A逆时针旋转，当点B恰好落在线段DG上时，请你帮他求出此时BE的长．
（3）如图3，若小明将正方形ABCD绕点A继续逆时针旋转，线段DG与线段BE将相交，交点为H，写出△
与△面积之和的最大值，并简要说明理由．27．如图，已知直线AB经过点（0，4），与抛物线y=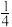
x2交于A，B两点，其中点A的横坐标是
．
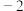(1）求这条直线的函数关系式及点B的坐标．
(2）在x轴上是否存在点C，使得△ABC是直角三角形？若存在，求出点C的坐标，若不存在请说明理由．
(3）过线段AB上一点P，作PM∥x轴，交抛物线于点M，点M在第一象限，点N（0，1），当点M的横坐标为何值时，MN+3MP的长度最大？最大值是多少？
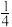x2交于A，B两点，其中点A的横坐标是
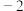．(1）求这条直线的函数关系式及点B的坐标．
(2）在x轴上是否存在点C，使得△ABC是直角三角形？若存在，求出点C的坐标，若不存在请说明理由．
(3）过线段AB上一点P，作PM∥x轴，交抛物线于点M，点M在第一象限，点N（0，1），当点M的横坐标为何值时，MN+3MP的长度最大？最大值是多少？
