全一卷
1.3的相反数是()
| A.﹣3 | B.3 | C. | D.﹣ |
2.右图是由四个小正方体叠成的一个立体图形,那么它的俯视图是( )


A. | B. | C. | D. |
3.据统计,2008年第一季度台州市国民生产总值约为41300000000元.数据41300000000用科学记数法可表示为()
A. | B. | C. | D. |
4.一组数据9.5,9,8.5,8,7.5的极差是()
| A.0.5 | B.8.5 | C.2.5 | D.2 |
5.不等式组 的解集在数轴上可表示为( )
的解集在数轴上可表示为( )
 的解集在数轴上可表示为( )
的解集在数轴上可表示为( )
6.如图,在菱形 中,对角线
中,对角线  相交于点
相交于点 为
为  的中点,且
的中点,且 ,则菱形
,则菱形  的周长为( )
的周长为( )

 中,对角线
中,对角线  相交于点
相交于点 为
为  的中点,且
的中点,且 ,则菱形
,则菱形  的周长为( )
的周长为( )
A. | B. | C. | D. |
7.四川5 12大地震后,灾区急需帐篷.某企业急灾区所急,准备捐助甲、乙两种型号的帐篷共2000顶,其中甲种帐篷每顶安置6人,乙种帐篷每顶安置4人,共安置9000人,设该企业捐助甲种帐篷
12大地震后,灾区急需帐篷.某企业急灾区所急,准备捐助甲、乙两种型号的帐篷共2000顶,其中甲种帐篷每顶安置6人,乙种帐篷每顶安置4人,共安置9000人,设该企业捐助甲种帐篷 顶、乙种帐篷
顶、乙种帐篷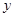 顶,那么下面列出的方程组中正确的是( )
顶,那么下面列出的方程组中正确的是( )
 12大地震后,灾区急需帐篷.某企业急灾区所急,准备捐助甲、乙两种型号的帐篷共2000顶,其中甲种帐篷每顶安置6人,乙种帐篷每顶安置4人,共安置9000人,设该企业捐助甲种帐篷
12大地震后,灾区急需帐篷.某企业急灾区所急,准备捐助甲、乙两种型号的帐篷共2000顶,其中甲种帐篷每顶安置6人,乙种帐篷每顶安置4人,共安置9000人,设该企业捐助甲种帐篷 顶、乙种帐篷
顶、乙种帐篷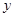 顶,那么下面列出的方程组中正确的是( )
顶,那么下面列出的方程组中正确的是( )A. | B. |
C. | D. |
8.下列命题中,正确的是( )
①顶点在圆周上的角是圆周角;②圆周角的度数等于圆心角度数的一半;③ 的圆周角所对的弦是直径;④不在同一条直线上的三个点确定一个圆;⑤同弧所对的圆周角相等
的圆周角所对的弦是直径;④不在同一条直线上的三个点确定一个圆;⑤同弧所对的圆周角相等
①顶点在圆周上的角是圆周角;②圆周角的度数等于圆心角度数的一半;③
 的圆周角所对的弦是直径;④不在同一条直线上的三个点确定一个圆;⑤同弧所对的圆周角相等
的圆周角所对的弦是直径;④不在同一条直线上的三个点确定一个圆;⑤同弧所对的圆周角相等| A.①②③ | B.③④⑤ | C.①②⑤ | D.②④⑤ |
9.课题研究小组对附着在物体表面的三个微生物(课题小组成员把他们分别标号为1,2,3)的生长情况进行观察记录.这三个微生物第一天各自一分为二,产生新的微生物(分别被标号为4,5,6,7,8,9),接下去每天都按照这样的规律变化,即每个微生物一分为二,形成新的微生物(课题组成员用如图所示的图形进行形象的记录).那么标号为100的微生物会出现在( )


| A.第3天 | B.第4天 | C.第5天 | D.第6天 |
10.把一个图形先沿着一条直线进行轴对称变换,再沿着与这条直线平行的方向平移,我们把这样的图形变换叫做滑动对称变换.在自然界和日常生活中,大量地存在这种图形变换(如图1).结合轴对称变换和平移变换的有关性质,你认为在滑动对称变换过程中,两个对应三角形(如图2)的对应点所具有的性质是( )


| A.对应点连线与对称轴垂直 |
| B.对应点连线被对称轴平分 |
| C.对应点连线被对称轴垂直平分 |
| D.对应点连线互相平行 |
11.化简:
_________ .

12.因式分解: .
.
 .
.13.台州市某中学随机调查了部分九年级学生的年龄,并画出了这些学生的年龄分布统计图(如图),那么,从该校九年级中任抽一名学生,抽到学生的年龄是16岁的概率是______ .


14.如图,从地面垂直向上抛出一小球,小球的高度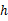 (单位:米)与小球运动时间
(单位:米)与小球运动时间 (单位:秒)的函数关系式是
(单位:秒)的函数关系式是 ,那么小球运动中的最大高度
,那么小球运动中的最大高度 .
.
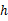 (单位:米)与小球运动时间
(单位:米)与小球运动时间 (单位:秒)的函数关系式是
(单位:秒)的函数关系式是 ,那么小球运动中的最大高度
,那么小球运动中的最大高度 .
.
15.如图,四边形 ,
,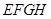 ,
, 都是正方形,边长分别为
都是正方形,边长分别为 ;
; 五点在同一直线上,则
五点在同一直线上,则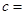
__________ (用含有 的代数式表示).
的代数式表示).

 ,
,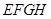 ,
, 都是正方形,边长分别为
都是正方形,边长分别为 ;
; 五点在同一直线上,则
五点在同一直线上,则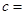
 的代数式表示).
的代数式表示).
16.善于归纳和总结的小明发现,“数形结合”是初中数学的基本思想方法,被广泛地应用在数学学习和解决问题中.用数量关系描述图形性质和用图形描述数量关系,往往会有新的发现.小明在研究垂直于直径的弦的性质过程中(如图,直径 弦
弦 于
于 ),设
),设 ,
, ,他用含
,他用含 的式子表示图中的弦
的式子表示图中的弦 的长度,通过比较运动的弦
的长度,通过比较运动的弦 和与之垂直的直径
和与之垂直的直径 的大小关系,发现了一个关于正数
的大小关系,发现了一个关于正数 的不等式,你也能发现这个不等式吗?写出你发现的不等式
的不等式,你也能发现这个不等式吗?写出你发现的不等式__________ .

 弦
弦 于
于 ),设
),设 ,
, ,他用含
,他用含 的式子表示图中的弦
的式子表示图中的弦 的长度,通过比较运动的弦
的长度,通过比较运动的弦 和与之垂直的直径
和与之垂直的直径 的大小关系,发现了一个关于正数
的大小关系,发现了一个关于正数 的不等式,你也能发现这个不等式吗?写出你发现的不等式
的不等式,你也能发现这个不等式吗?写出你发现的不等式
17.(1)计算: (2)解方程:
(2)解方程:
 (2)解方程:
(2)解方程:
18.如图,正方形网格中的每个小正方形的边长都是1,每个小正方形的顶点叫做格点. 的三个顶点
的三个顶点 都在格点上.
都在格点上.

(1)画出 绕点
绕点 逆时针旋转
逆时针旋转 后得到的三角形;
后得到的三角形;
(2)求 在上述旋转过程中所扫过的面积.
在上述旋转过程中所扫过的面积.
 的三个顶点
的三个顶点 都在格点上.
都在格点上.
(1)画出
 绕点
绕点 逆时针旋转
逆时针旋转 后得到的三角形;
后得到的三角形;(2)求
 在上述旋转过程中所扫过的面积.
在上述旋转过程中所扫过的面积.19.如图,一次函数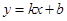 的图象与反比例函数
的图象与反比例函数 的图象交于
的图象交于 两点,直线
两点,直线 分别交
分别交 轴、
轴、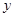 轴于
轴于 两点.
两点.

(1)求上述反比例函数和一次函数的解析式;
(2)求 的值.
的值.
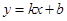 的图象与反比例函数
的图象与反比例函数 的图象交于
的图象交于 两点,直线
两点,直线 分别交
分别交 轴、
轴、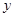 轴于
轴于 两点.
两点.
(1)求上述反比例函数和一次函数的解析式;
(2)求
 的值.
的值.20.在数学学习中,及时对知识进行归纳和整理是改善学习的重要方法.善于学习的小明在学习了一次方程(组)、一元一次不等式和一次函数后,把相关知识归纳整理如下:

(1)请你根据以上方框中的内容在下面数字序号后写出相应的结论:
① ;② ;③ ;④ ;
(2)如果点 的坐标为
的坐标为 ,那么不等式
,那么不等式 的解集是 .
的解集是 .

(1)请你根据以上方框中的内容在下面数字序号后写出相应的结论:
① ;② ;③ ;④ ;
(2)如果点
 的坐标为
的坐标为 ,那么不等式
,那么不等式 的解集是 .
的解集是 .
21.如图是某宾馆大厅到二楼的楼梯设计图,已知 米,
米, 米,中间平台宽度
米,中间平台宽度 为2米,
为2米, 为平台的两根支柱,
为平台的两根支柱, 垂直于
垂直于 ,垂足分别为
,垂足分别为 ,
, ,
, .求
.求 和
和 的水平距离
的水平距离 .(精确到0.1米,参考数据:
.(精确到0.1米,参考数据: ,
, )
)
 米,
米, 米,中间平台宽度
米,中间平台宽度 为2米,
为2米, 为平台的两根支柱,
为平台的两根支柱, 垂直于
垂直于 ,垂足分别为
,垂足分别为 ,
, ,
, .求
.求 和
和 的水平距离
的水平距离 .(精确到0.1米,参考数据:
.(精确到0.1米,参考数据: ,
, )
)
22.八年级(1)班开展了为期一周的“孝敬父母,帮做家务”社会活动,并根据学生帮家长做家务的时间来评价学生在活动中的表现,把结果划分成 五个等级.老师通过家长调查了全班50名学生在这次活动中帮父母做家务的时间,制作成如下的频数分布表和扇形统计图.
五个等级.老师通过家长调查了全班50名学生在这次活动中帮父母做家务的时间,制作成如下的频数分布表和扇形统计图.
学生帮父母做家务活动时间频数分布表

(1)求 的值;
的值;
(2)根据频数分布表估计该班学生在这次社会活动中帮父母做家务的平均时间;
(3)该班的小明同学这一周帮父母做家务2小时,他认为自己帮父母做家务的时间比班级里一半以上的同学多,你认为小明的判断符合实际吗?请用适当的统计量说明理由.
 五个等级.老师通过家长调查了全班50名学生在这次活动中帮父母做家务的时间,制作成如下的频数分布表和扇形统计图.
五个等级.老师通过家长调查了全班50名学生在这次活动中帮父母做家务的时间,制作成如下的频数分布表和扇形统计图.学生帮父母做家务活动时间频数分布表
| 等级 | 帮助父母做家务时间 (小时) | 频数 |
| A |  |  |
| B |  | 10 |
| C |  |  |
| D |  |  |
| E |  |  |

(1)求
 的值;
的值;(2)根据频数分布表估计该班学生在这次社会活动中帮父母做家务的平均时间;
(3)该班的小明同学这一周帮父母做家务2小时,他认为自己帮父母做家务的时间比班级里一半以上的同学多,你认为小明的判断符合实际吗?请用适当的统计量说明理由.
23. 经过
经过 顶点
顶点 的一条直线,
的一条直线, .
. 分别是直线
分别是直线 上两点,且
上两点,且 .
.
(1)若直线 经过
经过 的内部,且
的内部,且 在射线
在射线 上,请解决下面两个问题:
上,请解决下面两个问题:
①如图1,若 ,
, ,
,
则
 ;
;
 (填“
(填“ ”,“
”,“ ”或“
”或“ ”);
”);
②如图2,若 ,请添加一个关于
,请添加一个关于 与
与 关系的条件 ,使①中的两个结论仍然成立,并证明两个结论成立.
关系的条件 ,使①中的两个结论仍然成立,并证明两个结论成立.
(2)如图3,若直线 经过
经过 的外部,
的外部, ,请提出
,请提出 三条线段数量关系的合理猜想(不要求证明).
三条线段数量关系的合理猜想(不要求证明).

 经过
经过 顶点
顶点 的一条直线,
的一条直线, .
. 分别是直线
分别是直线 上两点,且
上两点,且 .
.(1)若直线
 经过
经过 的内部,且
的内部,且 在射线
在射线 上,请解决下面两个问题:
上,请解决下面两个问题:①如图1,若
 ,
, ,
,则

 ;
;
 (填“
(填“ ”,“
”,“ ”或“
”或“ ”);
”);②如图2,若
 ,请添加一个关于
,请添加一个关于 与
与 关系的条件 ,使①中的两个结论仍然成立,并证明两个结论成立.
关系的条件 ,使①中的两个结论仍然成立,并证明两个结论成立.(2)如图3,若直线
 经过
经过 的外部,
的外部, ,请提出
,请提出 三条线段数量关系的合理猜想(不要求证明).
三条线段数量关系的合理猜想(不要求证明).
24.如图,在矩形 中,
中, ,
, ,点
,点 是边
是边 上的动点(点
上的动点(点 不与点
不与点 ,点
,点 重合),过点
重合),过点 作直线
作直线 ,交
,交 边于
边于 点,再把
点,再把 沿着动直线
沿着动直线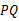 对折,点
对折,点 的对应点是
的对应点是 点,设
点,设 的长度为
的长度为 ,
, 与矩形
与矩形 重叠部分的面积为
重叠部分的面积为 .
.
(1)求 的度数;
的度数;
(2)当 取何值时,点
取何值时,点 落在矩形
落在矩形 的
的 边上?
边上?
(3)①求 与
与 之间的函数关系式;
之间的函数关系式;
②当 取何值时,重叠部分的面积等于矩形面积的
取何值时,重叠部分的面积等于矩形面积的 ?
?
 中,
中, ,
, ,点
,点 是边
是边 上的动点(点
上的动点(点 不与点
不与点 ,点
,点 重合),过点
重合),过点 作直线
作直线 ,交
,交 边于
边于 点,再把
点,再把 沿着动直线
沿着动直线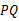 对折,点
对折,点 的对应点是
的对应点是 点,设
点,设 的长度为
的长度为 ,
, 与矩形
与矩形 重叠部分的面积为
重叠部分的面积为 .
.(1)求
 的度数;
的度数;(2)当
 取何值时,点
取何值时,点 落在矩形
落在矩形 的
的 边上?
边上?(3)①求
 与
与 之间的函数关系式;
之间的函数关系式;②当
 取何值时,重叠部分的面积等于矩形面积的
取何值时,重叠部分的面积等于矩形面积的 ?
?
 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
