全一卷
1.抛掷一枚硬币,正面向上的概率为( )
| A.1 | B. | C. | D. |
2.下图几何体的主视图是( )


A. | B. | C. | D. |
3.数据10,10,10,11,12,12,15,15的众数是()
| A.10 | B.11 | C.12 | D.15 |
4.不等式组 的解集为( )
的解集为( )
 的解集为( )
的解集为( )A. | B. | C. | D.无解 |
5.如图,若正六边形 绕着中心
绕着中心 旋转角
旋转角 得到的图形与原来的图形重合,则
得到的图形与原来的图形重合,则 最小值为( )
最小值为( )


 绕着中心
绕着中心 旋转角
旋转角 得到的图形与原来的图形重合,则
得到的图形与原来的图形重合,则 最小值为( )
最小值为( )

6.一个几何体的展开图如图所示,则该几何体的顶点有()


| A.10个 | B.8个 | C.6个 | D.4个 |
7.据2007年5月8日《台州晚报》报导,今年“五一”黄金周我市各旅游景点共接待游客约334万人,旅游总收入约9亿元.已知我市2005年“五一”黄金周旅游总收入约6.25亿元,那么这两年同期旅游总收入的年平均增长率约为( )
| A.12% | B.16% | C.20% | D.25% |
8.在同一坐标平面内,图象不可能由函数 的图象通过平移变换、轴对称变换得到的函数是( )
的图象通过平移变换、轴对称变换得到的函数是( )
 的图象通过平移变换、轴对称变换得到的函数是( )
的图象通过平移变换、轴对称变换得到的函数是( )A. | B. | C. | D. |
9.为确保信息安全,信息需要加密传输,发送方由明文 密文(加密),接收方由密文
密文(加密),接收方由密文  明文(解密).已知加密规则为:明文
明文(解密).已知加密规则为:明文 对应的密文a+1,b+4,3c+9.例如明文1,2,3对应的密文2,8,18.如果接收方收到密文7,18,15,则解密得到的明文为( )
对应的密文a+1,b+4,3c+9.例如明文1,2,3对应的密文2,8,18.如果接收方收到密文7,18,15,则解密得到的明文为( )
 密文(加密),接收方由密文
密文(加密),接收方由密文  明文(解密).已知加密规则为:明文
明文(解密).已知加密规则为:明文 对应的密文a+1,b+4,3c+9.例如明文1,2,3对应的密文2,8,18.如果接收方收到密文7,18,15,则解密得到的明文为( )
对应的密文a+1,b+4,3c+9.例如明文1,2,3对应的密文2,8,18.如果接收方收到密文7,18,15,则解密得到的明文为( )| A.4,5,6 | B.6,7,2 | C.2,6,7 | D.7,2,6 |
10.一次数学活动中,小迪利用自己制作的测角器测量小山的高度 .已知她的眼睛与地面的距离为1.6米,小迪在
.已知她的眼睛与地面的距离为1.6米,小迪在 处测量时,测角器中的
处测量时,测角器中的 (量角器零度线
(量角器零度线 和铅垂线
和铅垂线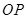 的夹角,如图);然后她向小山走50米到达点
的夹角,如图);然后她向小山走50米到达点 处(点
处(点 在同一直线上),这时测角器中的
在同一直线上),这时测角器中的 ,那么小山的高度
,那么小山的高度 约为()(注:数据
约为()(注:数据 ,供计算时选用)
,供计算时选用)

 .已知她的眼睛与地面的距离为1.6米,小迪在
.已知她的眼睛与地面的距离为1.6米,小迪在 处测量时,测角器中的
处测量时,测角器中的 (量角器零度线
(量角器零度线 和铅垂线
和铅垂线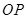 的夹角,如图);然后她向小山走50米到达点
的夹角,如图);然后她向小山走50米到达点 处(点
处(点 在同一直线上),这时测角器中的
在同一直线上),这时测角器中的 ,那么小山的高度
,那么小山的高度 约为()(注:数据
约为()(注:数据 ,供计算时选用)
,供计算时选用)
| A.68米 | B.70米 | C.121米 | D.123米 |
11.计算:(-2a)2=________ .
12.反比例函数 图象上一个点的坐标是
图象上一个点的坐标是______ .
 图象上一个点的坐标是
图象上一个点的坐标是13.如图,点 分别是
分别是 三边上的中点.若
三边上的中点.若 的面积为12,则
的面积为12,则 的面积为
的面积为_____ .

 分别是
分别是 三边上的中点.若
三边上的中点.若 的面积为12,则
的面积为12,则 的面积为
的面积为
14.两个装有乒乓球的盒子,其中一个装有2个白球1个黄球,另一个装有1个白球2个黄球.现从这两个盒中随机各取出一个球,则取出的两个球一个是白球一个是黄球的概率为___ .
15.(1)学习和研究《反比例函数的图象与性质》《一次函数的图象与性质》时,用到的数学思想方法有____ 、_____ (填2个即可).
(2)学数学不仅仅是听课和解题,三年初中数学学习期间,教材中给你留下深刻印象的选学内容、数学活动、课题学习有_____ 、_____ 、______ (填3个即可).
(2)学数学不仅仅是听课和解题,三年初中数学学习期间,教材中给你留下深刻印象的选学内容、数学活动、课题学习有
16.(1)善于思考的小迪发现:半径为 ,圆心在原点的圆(如图1),如果固定直径
,圆心在原点的圆(如图1),如果固定直径 ,把圆内的所有与
,把圆内的所有与 轴平行的弦都压缩到原来的
轴平行的弦都压缩到原来的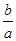 倍,就得到一种新的图形
倍,就得到一种新的图形 椭圆(如图2),她受祖冲之“割圆术”的启发,采用“化整为零,积零为整”“化曲为直,以直代曲”的方法.正确地求出了椭圆的面积,她求得的结果为
椭圆(如图2),她受祖冲之“割圆术”的启发,采用“化整为零,积零为整”“化曲为直,以直代曲”的方法.正确地求出了椭圆的面积,她求得的结果为_____ .
(2)小迪把图2的椭圆绕 轴旋转一周得到一个“鸡蛋型”的椭球.已知半径为
轴旋转一周得到一个“鸡蛋型”的椭球.已知半径为 的球的体积为
的球的体积为 ,则此椭球的体积为
,则此椭球的体积为______ .

 ,圆心在原点的圆(如图1),如果固定直径
,圆心在原点的圆(如图1),如果固定直径 ,把圆内的所有与
,把圆内的所有与 轴平行的弦都压缩到原来的
轴平行的弦都压缩到原来的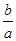 倍,就得到一种新的图形
倍,就得到一种新的图形 椭圆(如图2),她受祖冲之“割圆术”的启发,采用“化整为零,积零为整”“化曲为直,以直代曲”的方法.正确地求出了椭圆的面积,她求得的结果为
椭圆(如图2),她受祖冲之“割圆术”的启发,采用“化整为零,积零为整”“化曲为直,以直代曲”的方法.正确地求出了椭圆的面积,她求得的结果为(2)小迪把图2的椭圆绕
 轴旋转一周得到一个“鸡蛋型”的椭球.已知半径为
轴旋转一周得到一个“鸡蛋型”的椭球.已知半径为 的球的体积为
的球的体积为 ,则此椭球的体积为
,则此椭球的体积为
17.(1)解不等式: ;
;
(2).计算:
 ;
;(2).计算:

18.如图是建有平面直角坐标系的正方形网格,请按下列要求操作:

(1)画 ,使
,使 三点的坐标分别为
三点的坐标分别为 ;
;
(2) 种特殊的四边形?
种特殊的四边形?

(1)画
 ,使
,使 三点的坐标分别为
三点的坐标分别为 ;
;(2)
 种特殊的四边形?
种特殊的四边形?19.先化简,再求值: ,其中
,其中 .
.
 ,其中
,其中 .
.20.把正方形ABCD绕着点A,按顺时针方向旋转得到正方形AEFG,边FG与BC交于点H(如图).试问线段HG与线段HB相等吗?请先观察猜想,然后再证明你的猜想.


21.如图, 内接于
内接于 ,点
,点 在半径
在半径 的延长线上,
的延长线上, .
.
(1)试判断直线 与
与 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若 的半径长为1,求由弧
的半径长为1,求由弧 、线段
、线段 和
和 所围成的阴影部分面积(结果保留
所围成的阴影部分面积(结果保留 和根号).
和根号).
 内接于
内接于 ,点
,点 在半径
在半径 的延长线上,
的延长线上, .
.(1)试判断直线
 与
与 的位置关系,并说明理由;
的位置关系,并说明理由;(2)若
 的半径长为1,求由弧
的半径长为1,求由弧 、线段
、线段 和
和 所围成的阴影部分面积(结果保留
所围成的阴影部分面积(结果保留 和根号).
和根号).
22.台州某校七(1)班同学分三组进行数学活动,对七年级400名同学最喜欢喝的饮料情况、八年级300名同学零花钱的最主要用途情况、九年级300名同学完成家庭作业时间情况进行了全面调查,并分别用扇形图、频数分布直方图、表格来描述整理得到的数据.
根据以上信息,请回答下列问题:
(1)七年级400名同学中最喜欢喝“冰红茶”的人数是多少?
(2)补全八年级300名同学中零花钱的最主要用途情况频数分布直方图;
(3)九年级300名同学中完成家庭作业的平均时间大约是多少小时(结果保留一位小数)?


根据以上信息,请回答下列问题:
(1)七年级400名同学中最喜欢喝“冰红茶”的人数是多少?
(2)补全八年级300名同学中零花钱的最主要用途情况频数分布直方图;
(3)九年级300名同学中完成家庭作业的平均时间大约是多少小时(结果保留一位小数)?


23.善于不断改进学习方法的小迪发现,对解题进行回顾反思,学习效果更好.某一天小迪有20分钟时间可用于学习.假设小迪用于解题的时间 (单位:分钟)与学习收益量
(单位:分钟)与学习收益量 的关系如图1所示,用于回顾反思的时间
的关系如图1所示,用于回顾反思的时间 (单位:分钟)与学习收益
(单位:分钟)与学习收益 的关系如图2所示(其中
的关系如图2所示(其中 是抛物线的一部分,
是抛物线的一部分, 为抛物线的顶点),且用于回顾反思的时间不超过用于解题的时间.
为抛物线的顶点),且用于回顾反思的时间不超过用于解题的时间.

(1)求小迪解题的学习收益量 与用于解题的时间
与用于解题的时间 之间的函数关系式;
之间的函数关系式;
(2)求小迪回顾反思的学习收益量 与用于回顾反思的时间
与用于回顾反思的时间 的函数关系式;
的函数关系式;
(3)问小迪如何分配解题和回顾反思的时间,才能使这20分钟的学习收益总量最大?
 (单位:分钟)与学习收益量
(单位:分钟)与学习收益量 的关系如图1所示,用于回顾反思的时间
的关系如图1所示,用于回顾反思的时间 (单位:分钟)与学习收益
(单位:分钟)与学习收益 的关系如图2所示(其中
的关系如图2所示(其中 是抛物线的一部分,
是抛物线的一部分, 为抛物线的顶点),且用于回顾反思的时间不超过用于解题的时间.
为抛物线的顶点),且用于回顾反思的时间不超过用于解题的时间.
(1)求小迪解题的学习收益量
 与用于解题的时间
与用于解题的时间 之间的函数关系式;
之间的函数关系式;(2)求小迪回顾反思的学习收益量
 与用于回顾反思的时间
与用于回顾反思的时间 的函数关系式;
的函数关系式;(3)问小迪如何分配解题和回顾反思的时间,才能使这20分钟的学习收益总量最大?
24.如图,四边形 是一张放在平面直角坐标系中的矩形纸片,点
是一张放在平面直角坐标系中的矩形纸片,点 在
在 轴上,点
轴上,点 在
在 轴上,将边
轴上,将边 折叠,使点
折叠,使点 落在边
落在边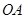 的点
的点 处.已知折叠
处.已知折叠 ,且
,且 .
.
(1)判断 与
与 是否相似?请说明理由;
是否相似?请说明理由;
(2)求直线 与
与 轴交点
轴交点 的坐标;
的坐标;
(3)是否存在过点 的直线
的直线 ,使直线
,使直线 、直线
、直线 与
与 轴所围成的三角形和直线
轴所围成的三角形和直线 、直线
、直线 与
与 轴所围成的三角形相似?如果存在,请直接写出其解析式并画出相应的直线;如果不存在,请说明理由.
轴所围成的三角形相似?如果存在,请直接写出其解析式并画出相应的直线;如果不存在,请说明理由.
 是一张放在平面直角坐标系中的矩形纸片,点
是一张放在平面直角坐标系中的矩形纸片,点 在
在 轴上,点
轴上,点 在
在 轴上,将边
轴上,将边 折叠,使点
折叠,使点 落在边
落在边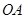 的点
的点 处.已知折叠
处.已知折叠 ,且
,且 .
.(1)判断
 与
与 是否相似?请说明理由;
是否相似?请说明理由;(2)求直线
 与
与 轴交点
轴交点 的坐标;
的坐标;(3)是否存在过点
 的直线
的直线 ,使直线
,使直线 、直线
、直线 与
与 轴所围成的三角形和直线
轴所围成的三角形和直线 、直线
、直线 与
与 轴所围成的三角形相似?如果存在,请直接写出其解析式并画出相应的直线;如果不存在,请说明理由.
轴所围成的三角形相似?如果存在,请直接写出其解析式并画出相应的直线;如果不存在,请说明理由.
 搜索
搜索
 难度系数:0.85
难度系数:0.85  答案解析
答案解析
 有奖纠错
有奖纠错
