全一卷
1.下列计算正确的是( )
| A.-1+2=1 | B.-1-1=0 | C.(-1)2=-1 | D.-12=1 |
2.∠A=60°,则∠A的补角是
| A.160° | B.120° | C.60° | D.30° |
3.如图是下列一个立体图形的三视图,则这个立体图形是()


| A.圆锥 | B.球 | C.圆柱 | D.正方体 |
4.掷一个质地均匀的正方体骰子,当骰子停止后,朝上一面的点数为5的概率是( )
| A.1 | B. | C. | D.0 |
5.如图所示,在⊙O中, =
= ,∠A=30°,则∠B=( )
,∠A=30°,则∠B=( )

 =
= ,∠A=30°,则∠B=( )
,∠A=30°,则∠B=( )
| A.150° | B.75° | C.60° | D.15° |
6.方程 的解是
的解是
 的解是
的解是| A.3 | B.2 | C.1 | D.0 |
7.在平面直角坐标系中,将线段OA向左平移2个单位,平移后,点O、A的对应点分别为点O1、A1.若点O(0,0),A(1,4),则点O1、A1的坐标分别是()
| A.(0,0),(1,4) | B.(0,0),(3,4) |
| C.(﹣2,0),(1,4) | D.(﹣2,0),(﹣1,4) |
8.计算:m2•m3=___ .
9.若式子 在实数范围内有意义,则x的取值范围是
在实数范围内有意义,则x的取值范围是_________ .
 在实数范围内有意义,则x的取值范围是
在实数范围内有意义,则x的取值范围是10.如图,在△ABC中,DE∥BC,AD=1,AB=3,DE=2,则BC=_____ .

11.在一次中学生田径运动会上,参加男子跳高的15名运动员成绩如下表
则这些运动员成绩的中位数是___ 米.
| 成绩(米) | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 |
| 人数(个) | 2 | 3 | 3 | 2 | 4 | 1 |
则这些运动员成绩的中位数是
12.x2﹣4x+4=(_______ )2.
13.已知反比例函数 的图象的一支位于第一象限,则常数m的取值范围是
的图象的一支位于第一象限,则常数m的取值范围是___ .
 的图象的一支位于第一象限,则常数m的取值范围是
的图象的一支位于第一象限,则常数m的取值范围是14.如图, ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=24厘米,△OAB的周长是18厘米,则EF=
ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=24厘米,△OAB的周长是18厘米,则EF=___ 厘米.
 ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=24厘米,△OAB的周长是18厘米,则EF=
ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点,若AC+BD=24厘米,△OAB的周长是18厘米,则EF=
15.某采石场爆破时,点燃导火线的甲工人要在爆破前转移到400米以外的安全区域.甲工人在转移过程中,前40米只能步行,之后骑自行车.已知导火线燃烧的速度为0.01米/秒,甲工人步行的速度为1米/秒,骑车的速度为4米/秒.为了确保甲工人的安全,则导火线的长要大于_____ 米.
16.如图,在平面直角坐标系中,点O是原点,点B(0, ),点A在第一象限且AB⊥BO,点E是线段AO的中点,点M在线段AB上.若点B和点E关于直线OM对称,则点M的坐标是(
),点A在第一象限且AB⊥BO,点E是线段AO的中点,点M在线段AB上.若点B和点E关于直线OM对称,则点M的坐标是(______ ).

 ),点A在第一象限且AB⊥BO,点E是线段AO的中点,点M在线段AB上.若点B和点E关于直线OM对称,则点M的坐标是(
),点A在第一象限且AB⊥BO,点E是线段AO的中点,点M在线段AB上.若点B和点E关于直线OM对称,则点M的坐标是(
17.(1)计算:5a+2b+(3a﹣2b);
(2)在平面直角坐标系中,已知点A(﹣4,1),B(﹣2,0),C(﹣3,﹣1).请在图1上画出△ABC,并画出与△ABC关于原点O对称的图形;

(3)如图所示,已知∠ACD=70°,∠ACB=60°,∠ABC=50°.求证:AB∥CD.
(2)在平面直角坐标系中,已知点A(﹣4,1),B(﹣2,0),C(﹣3,﹣1).请在图1上画出△ABC,并画出与△ABC关于原点O对称的图形;

(3)如图所示,已知∠ACD=70°,∠ACB=60°,∠ABC=50°.求证:AB∥CD.

18.(1)甲市共有三个郊县,各郊县的人数及人均耕地面积如表所示:
求甲市郊县所有人口的人均耕地面积(精确到0.01公顷);
(2)先化简下式,再求值: ,其中
,其中 ;
;
(3)如图,已知A,B,C,D是⊙O上的四点,延长DC,AB相交于点E,若BC=B

| 郊县 | 人数/万 | 人均耕地面积/公顷 |
| A | 20 | 0.15 |
| B | 5 | 0.20 |
| C | 10 | 0.18 |
求甲市郊县所有人口的人均耕地面积(精确到0.01公顷);
(2)先化简下式,再求值:
 ,其中
,其中 ;
;(3)如图,已知A,B,C,D是⊙O上的四点,延长DC,AB相交于点E,若BC=B
| A.求证:△ADE是等腰三角形. |

19.有一个质地均匀的正12面体,12个面上分别写有1~12这12个整数(每个面只有一个整数且互不相同).投掷这个正12面体一次,记事件A为“向上一面的数字是2或3的整数倍”,记事件B为“向上一面的数字是3的整数倍”,请你判断等式P(A)= +P(B)是否成立,并说明理由.
+P(B)是否成立,并说明理由.
 +P(B)是否成立,并说明理由.
+P(B)是否成立,并说明理由.20.如图,在梯形ABCD中,AD∥BC,对角线AC,BD相交于点E.若AE=4,CE=8,DE=3,梯形ABCD的高是 ,面积是54.求证:AC⊥BD.
,面积是54.求证:AC⊥BD.

 ,面积是54.求证:AC⊥BD.
,面积是54.求证:AC⊥BD.
21.一个有进水管与出水管的容器,从某时刻开始的3分内只进水不出水,在随后的9分内既进水又出水,每分的进水量和出水量都是常数,容器内的水量y(单位:升)与时间x(单位:分)之间的关系如图所示.当容器内的水量大于5升时,求时间x的取值范围.


22.如图所示,在正方形ABCD中,点G是边BC上任意一点,DE⊥AG,垂足为E,延长DE交AB于点F.在线段AG上取点H,使得AG=DE+HG,连接BH.求证:∠ABH=∠CDE.


23.已知点O是平面直角坐标系的原点,直线y=﹣x+m+n与双曲线 交于两个不同的点A(m,n)(m≥2)和B(p,q).直线y=﹣x+m+n与y轴交于点C,求△OBC的面积S的取值范围.
交于两个不同的点A(m,n)(m≥2)和B(p,q).直线y=﹣x+m+n与y轴交于点C,求△OBC的面积S的取值范围.
 交于两个不同的点A(m,n)(m≥2)和B(p,q).直线y=﹣x+m+n与y轴交于点C,求△OBC的面积S的取值范围.
交于两个不同的点A(m,n)(m≥2)和B(p,q).直线y=﹣x+m+n与y轴交于点C,求△OBC的面积S的取值范围.24.如图所示,已知四边形OABC是菱形,∠O=60°,点M是边OA的中点,以点O为圆心,r为半径作⊙O分别交OA,OC于点D,E,连接BM.若BM=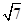 ,
, 的长是
的长是 .求证:直线BC与⊙O相切.
.求证:直线BC与⊙O相切.
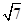 ,
, 的长是
的长是 .求证:直线BC与⊙O相切.
.求证:直线BC与⊙O相切.
25.若x1,x2是关于x的方程x2+bx+c=0的两个实数根,且|x1|+|x2|=2|k|(k是整数),则称方程x2+bx+c=0为“偶系二次方程”.如方程x2﹣6x﹣27=0,x2﹣2x﹣8=0, ,x2+6x﹣27=0,x2+4x+4=0,都是“偶系二次方程”.
,x2+6x﹣27=0,x2+4x+4=0,都是“偶系二次方程”.
(1)判断方程x2+x﹣12=0是否是“偶系二次方程”,并说明理由;
(2)对于任意一个整数b,是否存在实数c,使得关于x的方程x2+bx+c=0是“偶系二次方程”,并说明理由.
 ,x2+6x﹣27=0,x2+4x+4=0,都是“偶系二次方程”.
,x2+6x﹣27=0,x2+4x+4=0,都是“偶系二次方程”.(1)判断方程x2+x﹣12=0是否是“偶系二次方程”,并说明理由;
(2)对于任意一个整数b,是否存在实数c,使得关于x的方程x2+bx+c=0是“偶系二次方程”,并说明理由.
 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
