全一卷
1.-7的相反数是( )
| A.7 | B.-7 | C. | D. |
2.以下给出的几何体中,主视图是矩形,俯视图是圆的是( )
A. | B. | C. | D. |
3.2019年1月3日,“嫦娥四号”探测器成功着陆在月球背面东经177.6度、南纬45.5度附近,实现了人类首次在月球背面软着陆.数字177.6用科学记数法表示为( )
| A.0.1776×103 | B.1.776×102 | C.1.776×103 | D.17.76×102 |
4.如图, ,
, 平分
平分 ,若
,若 ,则
,则 的度数为( )
的度数为( )

 ,
, 平分
平分 ,若
,若 ,则
,则 的度数为( )
的度数为( )
A. | B. | C. | D. |
5.实数 在数轴上的对应点的位置如图所示,下列关系式不成立的是( )
在数轴上的对应点的位置如图所示,下列关系式不成立的是( )

 在数轴上的对应点的位置如图所示,下列关系式不成立的是( )
在数轴上的对应点的位置如图所示,下列关系式不成立的是( )
A. | B. | C. | D. |
6.下面的图形是用数学家名字命名的,其中既是轴对称图形又是中心对称图形的是( )
A. 赵爽弦图 赵爽弦图 | B. 笛卡尔心形线 笛卡尔心形线 |
C. 科克曲线 科克曲线 | D. 斐波那契螺旋线 斐波那契螺旋线 |
7.化简 的结果是( )
的结果是( )
 的结果是( )
的结果是( )A. | B. | C. | D. |
8.在学校的体育训练中,小杰投掷实心球的7次成绩如统计图所示,则这7次成绩的中位数和平均数分别是( )


A.9.7 ,9.9 ,9.9 | B.9.7 ,9.8 ,9.8 | C.9.8 ,9.7 ,9.7 | D.9.8 ,9.9 ,9.9 |
9.函数 与
与 (
( )在同一坐标系中的图象可能是( )
)在同一坐标系中的图象可能是( )
 与
与 (
( )在同一坐标系中的图象可能是( )
)在同一坐标系中的图象可能是( )A. | B. | C. | D. |
10.如图,在菱形 中,点
中,点 是
是 的中点,以
的中点,以 为圆心、
为圆心、 为半径作弧,交
为半径作弧,交 于点
于点 ,连接
,连接 .若
.若 ,
, ,则阴影部分的面积为( )
,则阴影部分的面积为( )

 中,点
中,点 是
是 的中点,以
的中点,以 为圆心、
为圆心、 为半径作弧,交
为半径作弧,交 于点
于点 ,连接
,连接 .若
.若 ,
, ,则阴影部分的面积为( )
,则阴影部分的面积为( )
A. | B. | C. | D. |
11.某数学社团开展实践性研究,在大明湖南门 测得历下亭
测得历下亭 在北偏东37°方向,继续向北走105m后到达游船码头
在北偏东37°方向,继续向北走105m后到达游船码头 ,测得历下亭
,测得历下亭 在游船码头
在游船码头 的北编东53°方向.请计算一下南门
的北编东53°方向.请计算一下南门 与历下亭
与历下亭 之间的距离约为( )(参考数据:
之间的距离约为( )(参考数据: ,
, )
)

 测得历下亭
测得历下亭 在北偏东37°方向,继续向北走105m后到达游船码头
在北偏东37°方向,继续向北走105m后到达游船码头 ,测得历下亭
,测得历下亭 在游船码头
在游船码头 的北编东53°方向.请计算一下南门
的北编东53°方向.请计算一下南门 与历下亭
与历下亭 之间的距离约为( )(参考数据:
之间的距离约为( )(参考数据: ,
, )
)
A.225 | B.275 | C.300 | D.315 |
12.关于 的一元二次方程
的一元二次方程 有一个根是﹣1,若二次函数
有一个根是﹣1,若二次函数 的图象的顶点在第一象限,设
的图象的顶点在第一象限,设 ,则
,则 的取值范围是( )
的取值范围是( )
 的一元二次方程
的一元二次方程 有一个根是﹣1,若二次函数
有一个根是﹣1,若二次函数 的图象的顶点在第一象限,设
的图象的顶点在第一象限,设 ,则
,则 的取值范围是( )
的取值范围是( )A. | B. | C. | D. |
13.分解因式:
_____ .

14.如图,一个可以自由转动的转盘,被分成了6个相同的扇形,转动转盘,转盘停止时,指针落在红色区域的概率等于_____ .


15.一个n边形的内角和是720°,则n=_____.
16.代数式 与代数式
与代数式 的和为4,则
的和为4,则
_____ .
 与代数式
与代数式 的和为4,则
的和为4,则
17.某市为提倡居民节约用水,自今年1月1日起调整居民用水价格.图中 、
、 分别表示去年、今年水费
分别表示去年、今年水费 (元)与用水量
(元)与用水量 (
( )之间的关系.小雨家去年用水量为150
)之间的关系.小雨家去年用水量为150 ,若今年用水量与去年相同,水费将比去年多
,若今年用水量与去年相同,水费将比去年多_____ 元.

 、
、 分别表示去年、今年水费
分别表示去年、今年水费 (元)与用水量
(元)与用水量 (
( )之间的关系.小雨家去年用水量为150
)之间的关系.小雨家去年用水量为150 ,若今年用水量与去年相同,水费将比去年多
,若今年用水量与去年相同,水费将比去年多
18.如图,在矩形纸片 中,将
中,将 沿
沿 翻折,使点
翻折,使点 落在
落在 上的点
上的点 处,
处, 为折痕,连接
为折痕,连接 ;再将
;再将 沿
沿 翻折,使点
翻折,使点 恰好落在
恰好落在 上的点
上的点 处,
处, 为折痕,连接
为折痕,连接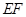 并延长交
并延长交 于点
于点 ,若
,若 ,
, ,则线段
,则线段 的长等于
的长等于_____ .

 中,将
中,将 沿
沿 翻折,使点
翻折,使点 落在
落在 上的点
上的点 处,
处, 为折痕,连接
为折痕,连接 ;再将
;再将 沿
沿 翻折,使点
翻折,使点 恰好落在
恰好落在 上的点
上的点 处,
处, 为折痕,连接
为折痕,连接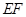 并延长交
并延长交 于点
于点 ,若
,若 ,
, ,则线段
,则线段 的长等于
的长等于
19.计算:

20.解不等式组 ,并写出它的所有整数解.
,并写出它的所有整数解.
 ,并写出它的所有整数解.
,并写出它的所有整数解.21.如图,在 中,
中, 分别是
分别是 和
和 上的点,
上的点, .求证:
.求证: .
.

 中,
中, 分别是
分别是 和
和 上的点,
上的点, .求证:
.求证: .
.
22.为提高学生的阅读兴趣,某学校建立了共享书架,并购买了一批书籍.其中购买 种图书花费了3000元,购买
种图书花费了3000元,购买 种图书花费了1600元,A种图书的单价是
种图书花费了1600元,A种图书的单价是 种图书的1.5倍,购买
种图书的1.5倍,购买 种图书的数量比
种图书的数量比 种图书多20本.
种图书多20本.
(1)求 和
和 两种图书的单价;
两种图书的单价;
(2)书店在“世界读书日”进行打折促销活动,所有图书都按8折销售学校当天购买了 种图书20本和
种图书20本和 种图书25本,共花费多少元?
种图书25本,共花费多少元?
 种图书花费了3000元,购买
种图书花费了3000元,购买 种图书花费了1600元,A种图书的单价是
种图书花费了1600元,A种图书的单价是 种图书的1.5倍,购买
种图书的1.5倍,购买 种图书的数量比
种图书的数量比 种图书多20本.
种图书多20本.(1)求
 和
和 两种图书的单价;
两种图书的单价;(2)书店在“世界读书日”进行打折促销活动,所有图书都按8折销售学校当天购买了
 种图书20本和
种图书20本和 种图书25本,共花费多少元?
种图书25本,共花费多少元?23.如图, 、
、 是
是 的两条直径,过点
的两条直径,过点 的
的 的切线交
的切线交 的延长线于点
的延长线于点 ,连接
,连接 、
、 .
.

(1)求证: ;
;
(2)若 是
是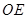 的中点,
的中点, ,求
,求 的半径.
的半径.
 、
、 是
是 的两条直径,过点
的两条直径,过点 的
的 的切线交
的切线交 的延长线于点
的延长线于点 ,连接
,连接 、
、 .
.
(1)求证:
 ;
;(2)若
 是
是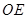 的中点,
的中点, ,求
,求 的半径.
的半径.24.某学校八年级共400名学生,为了解该年级学生的视力情况,从中随机抽取40名学生的视力数据作为样本,数据统计如下:
4.2 4.1 4.7 4.1 4.3 4.3 4.4 4.6 4.1 5.2
5.2 4.5 5.0 4.5 4.3 4.4 4.8 5.3 4.5 5.2
4.4 4.2 4.3 5.3 4.9 5.2 4.9 4.8 4.6 5.1
4.2 4.4 4.5 4.1 4.5 5.1 4.4 5.0 5.2 5.3
根据数据绘制了如下的表格和统计图:

根据上面提供的信息,回答下列问题:
(1)统计表中的 ,
, ;
;
(2)请补全条形统计图;
(3)根据抽样调查结果,请估计该校八年级学生视力为“ 级”的有多少人?
级”的有多少人?
(4)该年级学生会宣传部有2名男生和2名女生,现从中随机挑选2名同学参加“防控近视,爱眼护眼”宣传活动,请用树状图法或列表法求出恰好选中“1男1女”的概率.
4.2 4.1 4.7 4.1 4.3 4.3 4.4 4.6 4.1 5.2
5.2 4.5 5.0 4.5 4.3 4.4 4.8 5.3 4.5 5.2
4.4 4.2 4.3 5.3 4.9 5.2 4.9 4.8 4.6 5.1
4.2 4.4 4.5 4.1 4.5 5.1 4.4 5.0 5.2 5.3
根据数据绘制了如下的表格和统计图:
等级 | 视力(x) | 频数 | 频率 |
|
| 4 | 0.1 |
|
| 12 | 0.3 |
|
|
| |
|
|
| |
|
| 10 | 0.25 |
合计 | 40 | 1 | |

根据上面提供的信息,回答下列问题:
(1)统计表中的
 ,
, ;
;(2)请补全条形统计图;
(3)根据抽样调查结果,请估计该校八年级学生视力为“
 级”的有多少人?
级”的有多少人?(4)该年级学生会宣传部有2名男生和2名女生,现从中随机挑选2名同学参加“防控近视,爱眼护眼”宣传活动,请用树状图法或列表法求出恰好选中“1男1女”的概率.
25.如图1,点 、点
、点 在直线
在直线 上,反比例函数
上,反比例函数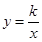 (
( )的图象经过点
)的图象经过点 .
.

(1)求 和
和 的值;
的值;
(2)将线段 向右平移
向右平移 个单位长度(
个单位长度( ),得到对应线段
),得到对应线段 ,连接
,连接 、
、 .
.
①如图2,当 时,过
时,过 作
作 轴于点
轴于点 ,交反比例函数图象于点
,交反比例函数图象于点 ,求
,求 的值;
的值;
②在线段 运动过程中,连接
运动过程中,连接 ,若
,若 是以
是以 为腰的等腰三形,求所有满足条件的
为腰的等腰三形,求所有满足条件的 的值.
的值.
 、点
、点 在直线
在直线 上,反比例函数
上,反比例函数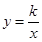 (
( )的图象经过点
)的图象经过点 .
.
(1)求
 和
和 的值;
的值;(2)将线段
 向右平移
向右平移 个单位长度(
个单位长度( ),得到对应线段
),得到对应线段 ,连接
,连接 、
、 .
.①如图2,当
 时,过
时,过 作
作 轴于点
轴于点 ,交反比例函数图象于点
,交反比例函数图象于点 ,求
,求 的值;
的值;②在线段
 运动过程中,连接
运动过程中,连接 ,若
,若 是以
是以 为腰的等腰三形,求所有满足条件的
为腰的等腰三形,求所有满足条件的 的值.
的值.26.小圆同学对图形旋转前后的线段之间、角之间的关系进行了拓展探究.

(一)猜测探究
在 中,
中, ,
, 是平面内任意一点,将线段
是平面内任意一点,将线段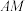 绕点
绕点 按顺时针方向旋转与
按顺时针方向旋转与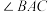 相等的角度,得到线段
相等的角度,得到线段 ,连接
,连接 .
.
(1)如图1,若 是线段
是线段 上的任意一点,请直接写出
上的任意一点,请直接写出 与
与 的数量关系是 ,
的数量关系是 , 与
与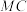 的数量关系是 ;
的数量关系是 ;
(2)如图2,点 是
是 延长线上点,若
延长线上点,若 是
是 内部射线
内部射线 上任意一点,连接
上任意一点,连接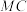 ,(1)中结论是否仍然成立?若成立,请给予证明,若不成立,请说明理由.
,(1)中结论是否仍然成立?若成立,请给予证明,若不成立,请说明理由.
(二)拓展应用
如图3,在 中,
中, ,
, ,
, ,
, 是
是 上的任意点,连接
上的任意点,连接 ,将
,将 绕点
绕点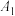 按顺时针方向旋转
按顺时针方向旋转 ,得到线段
,得到线段 ,连接
,连接 .求线段
.求线段 长度的最小值.
长度的最小值.

(一)猜测探究
在
 中,
中, ,
, 是平面内任意一点,将线段
是平面内任意一点,将线段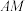 绕点
绕点 按顺时针方向旋转与
按顺时针方向旋转与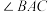 相等的角度,得到线段
相等的角度,得到线段 ,连接
,连接 .
.(1)如图1,若
 是线段
是线段 上的任意一点,请直接写出
上的任意一点,请直接写出 与
与 的数量关系是 ,
的数量关系是 , 与
与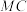 的数量关系是 ;
的数量关系是 ;(2)如图2,点
 是
是 延长线上点,若
延长线上点,若 是
是 内部射线
内部射线 上任意一点,连接
上任意一点,连接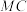 ,(1)中结论是否仍然成立?若成立,请给予证明,若不成立,请说明理由.
,(1)中结论是否仍然成立?若成立,请给予证明,若不成立,请说明理由.(二)拓展应用
如图3,在
 中,
中, ,
, ,
, ,
, 是
是 上的任意点,连接
上的任意点,连接 ,将
,将 绕点
绕点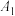 按顺时针方向旋转
按顺时针方向旋转 ,得到线段
,得到线段 ,连接
,连接 .求线段
.求线段 长度的最小值.
长度的最小值.27.如图1,抛物线 经过点
经过点 、
、 两点,
两点, 是其顶点,将抛物线
是其顶点,将抛物线 绕点
绕点 旋转
旋转 ,得到新的抛物线
,得到新的抛物线 .
.

(1)求抛物线 的函数解析式及顶点
的函数解析式及顶点 的坐标;
的坐标;
(2)如图2,直线 经过点
经过点 ,
, 是抛物线
是抛物线 上的一点,设
上的一点,设 点的横坐标为
点的横坐标为 (
( ),连接
),连接 并延长,交抛物线
并延长,交抛物线 于点
于点 ,交直线l于点
,交直线l于点 ,
, ,求
,求 的值;
的值;
(3)如图3,在(2)的条件下,连接 、
、 ,在直线
,在直线 下方的抛物线
下方的抛物线 上是否存在点
上是否存在点 ,使得
,使得 ?若存在,求出点
?若存在,求出点 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由.
 经过点
经过点 、
、 两点,
两点, 是其顶点,将抛物线
是其顶点,将抛物线 绕点
绕点 旋转
旋转 ,得到新的抛物线
,得到新的抛物线 .
.
(1)求抛物线
 的函数解析式及顶点
的函数解析式及顶点 的坐标;
的坐标;(2)如图2,直线
 经过点
经过点 ,
, 是抛物线
是抛物线 上的一点,设
上的一点,设 点的横坐标为
点的横坐标为 (
( ),连接
),连接 并延长,交抛物线
并延长,交抛物线 于点
于点 ,交直线l于点
,交直线l于点 ,
, ,求
,求 的值;
的值;(3)如图3,在(2)的条件下,连接
 、
、 ,在直线
,在直线 下方的抛物线
下方的抛物线 上是否存在点
上是否存在点 ,使得
,使得 ?若存在,求出点
?若存在,求出点 的横坐标;若不存在,请说明理由.
的横坐标;若不存在,请说明理由. 搜索
搜索
 难度系数:0.85
难度系数:0.85  答案解析
答案解析
 有奖纠错
有奖纠错








