搜索
全一卷
难度系数：0.94 
答案解析
有奖纠错
1．下列各数中，最小的是( )
| A．-2 | B．-0.1 | C．0 | D．|-1| |
2．如下是一种电子记分牌呈现的数字图形，其中既是轴对称图形又是中心对称图形的是( )
A． | B． | C． | D． |
3．一种花瓣的花粉颗粒直径约为0.0000065米，0.0000065用科学记数法表示为
A． | B． | C． | D． |
4．某校九年级8位同学一分钟跳绳的次数排序后如下：150,164,168,168,172,176,183,185，则有这组数据中得到的结论错误的是( )
| A．中位数为170 | B．众数为168 | C．极差为35 | D．平均数为170 |
5．在平面直角坐标系中，将抛物线
先向右平移2个单位，再向上平移2个单位，得到的抛物线解析式为
先向右平移2个单位，再向上平移2个单位，得到的抛物线解析式为A． | B． |
C． | D． |
6．如图所示的几何体的左视图是（ ）
A． | B． | C． | D． |
7．如图函数y=2x和y=ax+4的图象相交于A(m，3)，则不等式2x<ax+4的解集为
A． | B． | C． | D． |
8．如图，已知
为
的直径，
切于点A,
则下列结论不一定正确的是
为
的直径，
切于点A,
则下列结论不一定正确的是
A． | B． |
C． | D． |
9．计算：
________________
10．如图所示，在△ABC中，∠C=90°，∠CAB=50°，按以下步骤作图：①以点A为圆心，小于AC的长为半径画弧，分别交AB，AC于点E，F；②分别以点E，F为圆心，大于
EF的长为半径画弧，两弧相交于点G；③作射线AG交BC边于点D，则∠ADC的度数为____
EF的长为半径画弧，两弧相交于点G；③作射线AG交BC边于点D，则∠ADC的度数为11．母线长为3，底面圆的直径为2的圆锥的侧面积为
12．一个不透明的袋子中装有3个小球，它们除分别标有的数字1，3，5不同外，其他完全相同．任意从袋子中摸出一球后放回，在任意摸出一球，则两次摸出的球所标数字之和为6的概率是_______
13．如图，点A，B在反比例函数
的图像上，过点A，B作x轴的垂线，垂足分别为M，N，延长线段AB交x轴于点C，若OM=MN=NC，
的面积为6，则k值为____
的图像上，过点A，B作x轴的垂线，垂足分别为M，N，延长线段AB交x轴于点C，若OM=MN=NC，
的面积为6，则k值为
14．如图，在
中，
把△ABC绕AB边上的点D顺时针旋转90°得到△
，
交AB于点E，若AD=BE，则△
的面积为_______
中，
把△ABC绕AB边上的点D顺时针旋转90°得到△
，
交AB于点E，若AD=BE，则△
的面积为
15．如图，在
中，
．点D是BC边上一动点（不与点B、C重合），过点D作DE⊥BC交AB边于点E，将
沿直线DE翻折，点B落在射线BC上的点F处，当
AEF为直角三角形时，BD的长为________ ．
中，．点D是BC边上一动点（不与点B、C重合），过点D作DE⊥BC交AB边于点E，将沿直线DE翻折，点B落在射线BC上的点F处，当AEF为直角三角形时，BD的长为16．先化简
，然后从
的范围内选取一个合适的整数作为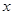
的值代入求值。
，然后从
的范围内选取一个合适的整数作为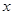
的值代入求值。17．5月31日是世界无烟日，某卫生机构为了了解“导致吸烟人比例高的最主要原因”，随机抽样调查了该市部分18~65岁的市,民，下图是根据调查结果绘制的统计图,根据图中信息解答下列问题：
（1）这次接受随机抽样调查的市民总人数为 ；
（2）图1中m 的值是 ；
（3）求图2中认为“烟民戒烟的毅力弱”所对应的圆心角的度数；
（4）若该市18~65岁的市民约有200万人，请你估算其中认为导致吸烟人口比例高的最主要原因是“对吸烟危害健康认识不足”的人数．
（1）这次接受随机抽样调查的市民总人数为 ；
（2）图1中m 的值是 ；
（3）求图2中认为“烟民戒烟的毅力弱”所对应的圆心角的度数；
（4）若该市18~65岁的市民约有200万人，请你估算其中认为导致吸烟人口比例高的最主要原因是“对吸烟危害健康认识不足”的人数．
18．如图，在菱形ABCD中，AB=2，∠DAB=60°，点E是AD边的中点，点M是AB边上一动点（不与点A重合），延长ME交射线CD于点N，连接MD，AN．
（1）求证：四边形AMDN是平行四边形；
（2）填空：①当AM的值为 时，四边形AMDN是矩形；②当AM的值为 时，四边形AMDN是菱形．
（1）求证：四边形AMDN是平行四边形；
（2）填空：①当AM的值为 时，四边形AMDN是矩形；②当AM的值为 时，四边形AMDN是菱形．
19．甲、乙两人同时从相距90千米的A地前往B地，甲乘汽车，乙骑摩托车，甲到达B地停留半个小时后返回A地，如图是他们离A地的距离
（千米）与
（时间）之间的函数关系图象．
(1)求甲从B地返回A地的过程中，与之间的函数关系式，并写出自变量的取值范围；
(2)若乙出发后2小时和甲相遇，求乙从A地到B地用了多长时间．
（千米）与（时间）之间的函数关系图象．(1)求甲从B地返回A地的过程中，
与之间的函数关系式，并写出自变量的取值范围；(2)若乙出发后2小时和甲相遇，求乙从A地到B地用了多长时间．
20．某宾馆为庆祝开业，在楼前悬挂了许多宣传条幅，如图所示，一条幅从楼顶A处放下，在楼前点C处拉直固定，小明为了测量此条幅的长度，他先在楼前D处测得楼顶A点的仰角为31°，再沿DB方向前进16米到达E处，测得点A的仰角为45°，已知点C到大厦的距离BC=7米，
,请根据以上数据求条幅的长度（结果保留整数.参考数据：
）
,请根据以上数据求条幅的长度（结果保留整数.参考数据：
）
21．某中学计划购买A型和B型课桌凳共200套，经招标，购买一套A型课桌凳比购买一套B型课桌凳少用40元，且购买4套A型和5套B型课桌凳共需1820元．
（1）求购买一套A型课桌凳和一套B型课桌凳各需多少元？
（2）学校根据实际情况，要求购买这两种课桌凳总费用不能超过40880元，并且购买A型课桌凳的数量不能超过B型课桌凳的
，求该校本次购买A型和B型课桌凳共有几种方案？哪种方案的总费用最低？
（1）求购买一套A型课桌凳和一套B型课桌凳各需多少元？
（2）学校根据实际情况，要求购买这两种课桌凳总费用不能超过40880元，并且购买A型课桌凳的数量不能超过B型课桌凳的
，求该校本次购买A型和B型课桌凳共有几种方案？哪种方案的总费用最低？22．类比、转化、从特殊到一般等思想方法，在数学学习和研究中经常用到，如下是一个案例，请补充完整.
原题：如图1，在
中，点E是BC边上的中点，点F是线段AE上一点，BF的延长线交射线CD于点G，若
，求
的值．
（1）尝试探究
在图1中，过点E作
交BG于点H，则AB和EH的数量关系是 ，CG和EH的数量关系是 ，的值是
（2）类比延伸
如图2，在原题的条件下，若
则的值是 （用含
的代数式表示），试写出解答过程．
（3）拓展迁移
如图3，梯形ABCD中，DC∥AB，点E是BC延长线上一点，AE和BD相交于点F，若
，则
的值是 （用含
的代数式表示）.
原题：如图1，在
中，点E是BC边上的中点，点F是线段AE上一点，BF的延长线交射线CD于点G，若
，求
的值．
（1）尝试探究
在图1中，过点E作
交BG于点H，则AB和EH的数量关系是 ，CG和EH的数量关系是 ，的值是 （2）类比延伸
如图2，在原题的条件下，若
则的值是 （用含
的代数式表示），试写出解答过程．
（3）拓展迁移
如图3，梯形ABCD中，DC∥AB，点E是BC延长线上一点，AE和BD相交于点F，若
，则
的值是 （用含
的代数式表示）.
23．如图，在平面直角坐标系中，直线
与抛物线
交于A，B两点，点A在x轴上，点B的纵坐标为3，点P是直线AB下方的抛物线上一动点（不与A，B重合），过点P作x轴的垂线交直线AB与点C，作PD⊥AB于点D
(1)求
及
的值
(2)设点P的横坐标为m
①用含
的代数式表示线段PD的长，并求出线段PD长的最大值；
②连接PB，线段PC把
分成两个三角形，是否存在适合的m值，使这两个三角形的面积之比为9：10？若存在，直接写出m值；若不存在，说明理由．
与抛物线
交于A，B两点，点A在x轴上，点B的纵坐标为3，点P是直线AB下方的抛物线上一动点（不与A，B重合），过点P作x轴的垂线交直线AB与点C，作PD⊥AB于点D
(1)求
及
的值(2)设点P的横坐标为m
①用含
的代数式表示线段PD的长，并求出线段PD长的最大值；②连接PB，线段PC把
分成两个三角形，是否存在适合的m值，使这两个三角形的面积之比为9：10？若存在，直接写出m值；若不存在，说明理由．