全一卷
1. 的倒数是()
的倒数是()
 的倒数是()
的倒数是()| A.2 | B. | C. | D. |
2.下列电视台的台标,是中心对称图形的是( )
A. | B. | C. | D. |
3.若 ,则下列式子中错误的是()
,则下列式子中错误的是()
 ,则下列式子中错误的是()
,则下列式子中错误的是()A. | B. | C. | D. |
4.在我国南海某海域探明可燃冰储量约有194亿立方米.数字19 400 000 000用科学记数法表示正确的是()
A. | B. | C. | D. |
5.下列各式计算正确的是()
A. | B. |
C. | D. |
6.如图,能判定 的条件是()
的条件是()

 的条件是()
的条件是()
A. | B. |
C. | D. |
7.在Rt 中,
中, ,若
,若 ,则
,则 的值是( )
的值是( )
 中,
中, ,若
,若 ,则
,则 的值是( )
的值是( )A. | B. | C. | D. |
8.汽车以60千米/时的速度在公路上匀速行驶,1小时后进入高速路,继续以100千米/时的速度匀速行驶,则汽车行驶的路程s(千米)与行驶的时间t(时)的函数关系的大致图象是( )
A. | B. | C. | D. |
9.如图是一个正方体展开图,把展开图折叠成正方体后,“你”字一面相对面上的字是( )


| A.我 | B.中 | C.国 | D.梦 |
10.已知直线 ,若
,若 ,
, ,那么该直线不经过( )
,那么该直线不经过( )
 ,若
,若 ,
, ,那么该直线不经过( )
,那么该直线不经过( )| A.第一象限 | B.第二象限 | C.第三象限 | D.第四象限 |
11.4的平方根是_______ .
12.已知 ,
, ,则
,则
______________
 ,
, ,则
,则
13.已知 为平面内三条不同直线,若
为平面内三条不同直线,若 ,
, ,则
,则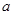 与
与 的位置关系是
的位置关系是
 为平面内三条不同直线,若
为平面内三条不同直线,若 ,
, ,则
,则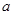 与
与 的位置关系是
的位置关系是 14.小明在射击训练中,五次命中的环数分别为5,7,6,6,6,则小明命中环数的众数为__________________ ,平均数为_____________________
15.写出一个在三视图中俯视图与主视图完全相同的几何体
16.如图,把 绕点C按顺时针方向旋转
绕点C按顺时针方向旋转 ,得到
,得到 ,
, 交
交 于点D,若
于点D,若 ,则
,则
___________________ °.

 绕点C按顺时针方向旋转
绕点C按顺时针方向旋转 ,得到
,得到 ,
, 交
交 于点D,若
于点D,若 ,则
,则

17.计算: .
.
 .
.18.已知反比例函数 的图象经过点M(2,1).
的图象经过点M(2,1).
(1)求该函数的表达式;
(2)当 时,求
时,求 的取值范围.(直接写出结果)
的取值范围.(直接写出结果)
 的图象经过点M(2,1).
的图象经过点M(2,1).(1)求该函数的表达式;
(2)当
 时,求
时,求 的取值范围.(直接写出结果)
的取值范围.(直接写出结果)19.如图,在Rt 中,
中, ,分别以点A、C为圆心,大于
,分别以点A、C为圆心,大于 长为半径画弧,两弧相交于点M、N,连结MN,与AC、BC分别交于点D、E,连结AE.
长为半径画弧,两弧相交于点M、N,连结MN,与AC、BC分别交于点D、E,连结AE.
(1)求 ;(直接写出结果)
;(直接写出结果)
(2)当AB=3,AC=5时,求 的周长.
的周长.
 中,
中, ,分别以点A、C为圆心,大于
,分别以点A、C为圆心,大于 长为半径画弧,两弧相交于点M、N,连结MN,与AC、BC分别交于点D、E,连结AE.
长为半径画弧,两弧相交于点M、N,连结MN,与AC、BC分别交于点D、E,连结AE.(1)求
 ;(直接写出结果)
;(直接写出结果)(2)当AB=3,AC=5时,求
 的周长.
的周长.
20.如图,在□ABCD中,E是AD边上的中点,连接BE并延长交CD的延长线于点F.
(1)证明:FD=AB;
(2)当平行四边形ABCD的面积为8时,求△FED的面积.
(1)证明:FD=AB;
(2)当平行四边形ABCD的面积为8时,求△FED的面积.

21.一个口袋中有3个大小相同的小球,球面上分别写有数字1、2、3.从袋中随机地摸出一个小球,记录下数字后放回,再随机地摸出一个小球.
(1)请用树形图或列表法中的一种,列举出两次摸出的球上数字的所有可能结果;
(2)求两次摸出的球上的数字和为偶数的概率.
(1)请用树形图或列表法中的一种,列举出两次摸出的球上数字的所有可能结果;
(2)求两次摸出的球上的数字和为偶数的概率.
22.已知关于x的方程 .
.
(1)若该方程的一个根为1,求a的值及该方程的另一根;
(2)求证:不论a取何实数,该方程都有两个不相等的实数根.
 .
.(1)若该方程的一个根为1,求a的值及该方程的另一根;
(2)求证:不论a取何实数,该方程都有两个不相等的实数根.
23.某校为美化校园,计划对面积为1800m2的区域进行绿化,安排甲、乙两个工程队完成.已知甲队每天能完成绿化的面积是乙队每天能完成绿化的面积的2倍,并且在独立完成面积为400 m2区域的绿化时,甲队比乙队少用4天.
(1)求甲、乙两工程队每天能完成绿化的面积分别是多少m2?
(2)若学校每天需付给甲队的绿化费用为0.4万元,乙队为0.25万元,要使这次的绿化总费用不超过8万元,至少应安排甲队工作多少天?
(1)求甲、乙两工程队每天能完成绿化的面积分别是多少m2?
(2)若学校每天需付给甲队的绿化费用为0.4万元,乙队为0.25万元,要使这次的绿化总费用不超过8万元,至少应安排甲队工作多少天?
24.如图,在Rt 中,
中, ,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.
,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.
(1)求证:点E是边BC的中点;
(2)求证: ;
;
(3)当以点O、D、E、C为顶点的四边形是正方形时,求证:△ABC是等腰直角三角形.

 中,
中, ,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.
,以AC为直径的⊙O与AB边交于点D,过点D作⊙O的切线,交BC于E.(1)求证:点E是边BC的中点;
(2)求证:
 ;
;(3)当以点O、D、E、C为顶点的四边形是正方形时,求证:△ABC是等腰直角三角形.

25.如图,已知抛物线 与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
(1)直接写出A、D、C三点的坐标;
(2)若点M在抛物线上,使得△MAD的面积与△CAD的面积相等,求点M的坐标;
(3)设点C关于抛物线对称轴的对称点为B,在抛物线上是否存在点P,使得以A、B、C、P四点为顶点的四边形为梯形?若存在,请求出点P的坐标;若不存在,请说明理由.

 与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.
与x轴的交点为A、D(A在D的右侧),与y轴的交点为C.(1)直接写出A、D、C三点的坐标;
(2)若点M在抛物线上,使得△MAD的面积与△CAD的面积相等,求点M的坐标;
(3)设点C关于抛物线对称轴的对称点为B,在抛物线上是否存在点P,使得以A、B、C、P四点为顶点的四边形为梯形?若存在,请求出点P的坐标;若不存在,请说明理由.

 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
