全一卷
1.-2的倒数是( )
| A.-2 | B. | C. | D.2 |
2.下图是一个六角棱栓,它的主视图和俯视图都正确的是( )


A. | B. |
C. | D. |
3.下列运算正确的是( )
A. | B. |
C. | D. |
4.(3分)不等式组 的解集在数轴上表示正确的是()
的解集在数轴上表示正确的是()
 的解集在数轴上表示正确的是()
的解集在数轴上表示正确的是()A. |
B. |
C. |
D. |
5.某企业为了解员工给灾区“爱心捐款”的情况,随机抽取部分员工的捐款金额整理绘制成如图所示的直方图,根据图中信息,下列结论正确的是( )


| A.样本中位数是200元 |
| B.样本容量是20 |
| C.该企业员工捐款金额的极差是450元 |
| D.该企业员工最大捐款金额是500元 |
6.方程 的解是( )
的解是( )
 的解是( )
的解是( )| A.x=2 | B.x=1 | C.x=0 | D.无实数解 |
7.如图,双曲线y=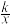 与直线y=﹣
与直线y=﹣ x交于A、B两点,且A(﹣2,m),则点B的坐标是( )
x交于A、B两点,且A(﹣2,m),则点B的坐标是( )

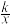 与直线y=﹣
与直线y=﹣ x交于A、B两点,且A(﹣2,m),则点B的坐标是( )
x交于A、B两点,且A(﹣2,m),则点B的坐标是( )
| A.(2,﹣1) | B.(1,﹣2) | C.( ,﹣1) ,﹣1) | D.(﹣1, ) ) |
8.如图,正方形OABC绕着点O逆时针旋转40°得到正方形ODEF,连接AF,则∠OFA的度数是( ).


| A.15° | B.20° | C.25° | D.30° |
9.2015年云南省约有272000名学生参加高考,272000用科学记数法表示为2.72×10n,则n=_____ .
10.若平行四边形中两个内角的度数比为1:2,则其中较大的内角是_________ 度.
11.若 ADE∽
ADE∽ ACB,且
ACB,且 ,DE=10,则BC=
,DE=10,则BC= _______ .

 ADE∽
ADE∽ ACB,且
ACB,且 ,DE=10,则BC=
,DE=10,则BC= 
12.如图,在半径为3的⊙O中,直径AB与弦CD相交于点E,连接AC,B

| A.若AC=2,则cosD= |

13.一个不透明的盒子里装有除颜色外无其他差别的白珠子6颗和黑珠子若干颗,每次随机摸出一颗珠子,放回摇匀后再摸,通过多次试验发现摸到白珠子的频率稳定在0.3左右,则盒子中黑珠子可能有__ 颗.
14.一元二次方程 有两个不相等的实数根且两根之积为正数,若c是整数,则c=
有两个不相等的实数根且两根之积为正数,若c是整数,则c=_____ .(只需填一个).
 有两个不相等的实数根且两根之积为正数,若c是整数,则c=
有两个不相等的实数根且两根之积为正数,若c是整数,则c=15.用火柴棒按下图所示的方式摆大小不同的“H”:

依此规律,摆出第9个“H”需用火柴棒_______ 根.

依此规律,摆出第9个“H”需用火柴棒
16.如图,在Rt△ABC中,∠C=30°,以直角顶点A为圆心,AB长为半径画弧交BC于点D,过D作DE⊥AC于点E.若DE=a,则△ABC的周长用含a的代数式表示为________________ .


17.计算: .
.
 .
.18.先化简,再求值: ),其中
),其中 .
.
 ),其中
),其中 .
.19.节约用水是我们的美德,水龙头关闭不严会造成滴水,容器内盛水 与滴水时间
与滴水时间 的关系用可以显示水量的容器做如图
的关系用可以显示水量的容器做如图 的试验,并根据试验数据绘制出如图
的试验,并根据试验数据绘制出如图 的函数图象,结合图象解答下列问题.
的函数图象,结合图象解答下列问题.
( )容器内原有水多少升.
)容器内原有水多少升.
( )求
)求 与
与 之间的函数关系式,并计算在这种滴水状态下一天的滴水量是多少升.
之间的函数关系式,并计算在这种滴水状态下一天的滴水量是多少升.

 与滴水时间
与滴水时间 的关系用可以显示水量的容器做如图
的关系用可以显示水量的容器做如图 的试验,并根据试验数据绘制出如图
的试验,并根据试验数据绘制出如图 的函数图象,结合图象解答下列问题.
的函数图象,结合图象解答下列问题.(
 )容器内原有水多少升.
)容器内原有水多少升.(
 )求
)求 与
与 之间的函数关系式,并计算在这种滴水状态下一天的滴水量是多少升.
之间的函数关系式,并计算在这种滴水状态下一天的滴水量是多少升.
20.某商场投入13800元资金购进甲、乙两种矿泉水共500箱,矿泉水的成本价和销售价如表所示:
(1)该商场购进甲、乙两种矿泉水各多少箱?
(2)全部售完500箱矿泉水,该商场共获得利润多少元?
| 类别/单价 | 成本价 | 销售价(元/箱) |
| 甲 | 24 | 36 |
| 乙 | 33 | 48 |
(1)该商场购进甲、乙两种矿泉水各多少箱?
(2)全部售完500箱矿泉水,该商场共获得利润多少元?
21.如图,菱形ABCD的对角线AC与BD相交于点O,且BE∥AC,CE∥BD.
(1)求证:四边形OBEC是矩形;
(2)若菱形ABCD的周长是 ,
, ,求四边形OBEC的面积.
,求四边形OBEC的面积.
(1)求证:四边形OBEC是矩形;
(2)若菱形ABCD的周长是
 ,
, ,求四边形OBEC的面积.
,求四边形OBEC的面积.
22.(10分)某中学需在短跑、跳远、乒乓球、跳高四类体育项目中各选一名同学参加中学生运动会,根据平时成绩,把各项目进入复选的人员情况绘制成不完整的统计图、表如下:复选人员扇形统计图:复选人员统计表:


(1)求a、b的值;
(2)求扇形统计图中跳远项目对应圆心角的度数;
(3)用列表法或画树状图的方法求在短跑和乒乓球项目中选出的两位同学都为男生的概率.


(1)求a、b的值;
(2)求扇形统计图中跳远项目对应圆心角的度数;
(3)用列表法或画树状图的方法求在短跑和乒乓球项目中选出的两位同学都为男生的概率.
23.如图,过∠AOB的平分线上一点C作CD∥OB交OA于点D,E是线段OC的中点,过点E作直线分别交射线CD,OB于点M,N,探究线段OD,ON,DM之间的数量关系,并证明你的结论.


24.如图,在平面直角坐标系xOy中,直线l⊥y轴于点B(0,﹣2),A为OB的中点,以A为顶点的抛物线 与x轴交于C、D两点,且CD=4,点P为抛物线上的一个动点,以P为圆心,PO为半径画圆.
与x轴交于C、D两点,且CD=4,点P为抛物线上的一个动点,以P为圆心,PO为半径画圆.

(1)求抛物线的解析式;
(2)若⊙P与y轴的另一交点为E,且OE=2,求点P的坐标;
(3)判断直线l与⊙P的位置关系,并说明理由.
 与x轴交于C、D两点,且CD=4,点P为抛物线上的一个动点,以P为圆心,PO为半径画圆.
与x轴交于C、D两点,且CD=4,点P为抛物线上的一个动点,以P为圆心,PO为半径画圆.
(1)求抛物线的解析式;
(2)若⊙P与y轴的另一交点为E,且OE=2,求点P的坐标;
(3)判断直线l与⊙P的位置关系,并说明理由.
 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
