全一卷
1.下列运算正确的是( )
A. | B. | C.a2 | D. |
2.将 用小数表示为().
用小数表示为().
 用小数表示为().
用小数表示为().| A.0.000 000 005 62 | B.0.000 000 056 2 | C.0.000 000 562 | D.0.000 000 000 562 |
3.如图,数轴上A,B两点对应的实数分别是1和 ,若A点关于B点的对称点为点C,则点C所对应的实数为( )
,若A点关于B点的对称点为点C,则点C所对应的实数为( )

 ,若A点关于B点的对称点为点C,则点C所对应的实数为( )
,若A点关于B点的对称点为点C,则点C所对应的实数为( )
A.2 -1 -1 | B.1+ | C.2+ | D.2 +1 +1 |
4.如图, 是
是 的弦,半径
的弦,半径 于点
于点 且
且
 则
则 的长为( ).
的长为( ).

 是
是 的弦,半径
的弦,半径 于点
于点 且
且
 则
则 的长为( ).
的长为( ).
A. | B. | C. | D. |
5.二元一次方程组 的解是().
的解是().
 的解是().
的解是().A. | B. |
C. | D. |
6.关于 的一元二次方程
的一元二次方程 有两个不相等的实数根,则实数
有两个不相等的实数根,则实数 的取值范围是( ).
的取值范围是( ).
 的一元二次方程
的一元二次方程 有两个不相等的实数根,则实数
有两个不相等的实数根,则实数 的取值范围是( ).
的取值范围是( ).A. | B. | C. | D. |
7.如图,雷达探测器测得六个目标 出现.按照规定的目标表示方法,目标
出现.按照规定的目标表示方法,目标 的位置表示为
的位置表示为 按照此方法在表示目标
按照此方法在表示目标 的位置时,其中表示不正确的是( ).
的位置时,其中表示不正确的是( ).

 出现.按照规定的目标表示方法,目标
出现.按照规定的目标表示方法,目标 的位置表示为
的位置表示为 按照此方法在表示目标
按照此方法在表示目标 的位置时,其中表示不正确的是( ).
的位置时,其中表示不正确的是( ).
A. | B. |
C. | D. |
8.如图,已知矩形 一条直线将该矩形
一条直线将该矩形 分割成两个多边形(含三角形),若这两个多边形的内角和分别为
分割成两个多边形(含三角形),若这两个多边形的内角和分别为 和
和 则
则 不可能是( ).
不可能是( ).

 一条直线将该矩形
一条直线将该矩形 分割成两个多边形(含三角形),若这两个多边形的内角和分别为
分割成两个多边形(含三角形),若这两个多边形的内角和分别为 和
和 则
则 不可能是( ).
不可能是( ).
A. | B. | C. | D. |
9.已知函数 与函数
与函数 的图象大致如图.若
的图象大致如图.若 则自变量
则自变量 的取值范围是( ).
的取值范围是( ).

 与函数
与函数 的图象大致如图.若
的图象大致如图.若 则自变量
则自变量 的取值范围是( ).
的取值范围是( ).
A. | B. |
C. | D. |
10.已知一个圆锥的侧面展开图是一个半径为9,圆心角为120°的扇形,则该圆锥的底面半径等于( )
| A.9 | B.27 | C.3 | D.10 |
11.若正比例函数y=2kx与反比例函数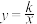 (k≠0)的图象交于点A(m,1),则k的值是( )
(k≠0)的图象交于点A(m,1),则k的值是( )
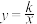 (k≠0)的图象交于点A(m,1),则k的值是( )
(k≠0)的图象交于点A(m,1),则k的值是( )A. 或 或 | B. 或 或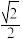 | C.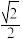 | D. |
12.如图所示,一般书本的纸张是在原纸张多次对开得到的.矩形 沿
沿 对开后,再把矩形
对开后,再把矩形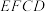 沿
沿 对开,依此类推.若各种开本的矩形都相似,那么
对开,依此类推.若各种开本的矩形都相似,那么 等于( ).
等于( ).

 沿
沿 对开后,再把矩形
对开后,再把矩形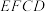 沿
沿 对开,依此类推.若各种开本的矩形都相似,那么
对开,依此类推.若各种开本的矩形都相似,那么 等于( ).
等于( ).
A. | B.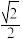 | C. | D. |
13.分式方程 的解是
的解是_________
 的解是
的解是14.分解因式: _________.
_________.
 _________.
_________.15.有4张背面相同的扑克牌,正面数字分别为2,3,4,5.若将这4张扑克牌背面向上洗匀后,从中任意抽取一张,放回后洗匀,再从中任意抽取一张.这两张扑克牌正面数字之和是3的倍数的概率为_________.
16.如图,在 中,
中, 是
是 边上一点,过点
边上一点,过点 作
作 交
交 于点E,过点
于点E,过点 作
作 交
交 于点
于点 ,则四边形
,则四边形 的周长是
的周长是_________

 中,
中, 是
是 边上一点,过点
边上一点,过点 作
作 交
交 于点E,过点
于点E,过点 作
作 交
交 于点
于点 ,则四边形
,则四边形 的周长是
的周长是
17.直角梯形 中,
中,



 点
点 在
在 上,将
上,将 沿
沿 翻折,使
翻折,使 点与
点与 点重合,则
点重合,则 的正切值是
的正切值是_________

 中,
中,



 点
点 在
在 上,将
上,将 沿
沿 翻折,使
翻折,使 点与
点与 点重合,则
点重合,则 的正切值是
的正切值是
18.2010年5月1日至20日的20天里,每天参观上海世博会的人数统计如下:(单位:万人次)
20,22,13,15,11,11,14,20,14,16,
18,18,22,24,34,24,24,26,29,30.
(1)写出以上20个数据的众数、中位数、平均数;
(2)若按照前20天参观人数的平均数计算,估计上海世博会期间(2010年5月1日至2010年10月31日)参观的总人数约是多少万人次?
(3)要达到组委会预计的参观上海世博会的总人数约为7000万人次,2010年5月21日至2010年10月31日期间,平均每天参观人数约为多少万人次?(结果精确到0.01万人次)
20,22,13,15,11,11,14,20,14,16,
18,18,22,24,34,24,24,26,29,30.
(1)写出以上20个数据的众数、中位数、平均数;
(2)若按照前20天参观人数的平均数计算,估计上海世博会期间(2010年5月1日至2010年10月31日)参观的总人数约是多少万人次?
(3)要达到组委会预计的参观上海世博会的总人数约为7000万人次,2010年5月21日至2010年10月31日期间,平均每天参观人数约为多少万人次?(结果精确到0.01万人次)
19.如图, 是
是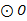 的直径,
的直径, 是
是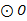 上的两点,且
上的两点,且

(1)求证:
(2)若 将四边形
将四边形 分成面积相等的两个三角形,试确定四边形
分成面积相等的两个三角形,试确定四边形 的形状.
的形状.
 是
是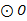 的直径,
的直径, 是
是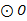 上的两点,且
上的两点,且

(1)求证:

(2)若
 将四边形
将四边形 分成面积相等的两个三角形,试确定四边形
分成面积相等的两个三角形,试确定四边形 的形状.
的形状.20.某中学的高中部在 校区,初中部在
校区,初中部在 校区,学校学生会计划在3月12日植树节当天安排部分学生到郊区公园参加植树活动.已知
校区,学校学生会计划在3月12日植树节当天安排部分学生到郊区公园参加植树活动.已知 校区的每位高中学生往返车费是6元,每人每天可栽植5棵树;
校区的每位高中学生往返车费是6元,每人每天可栽植5棵树; 校区的每位初中学生往返车费是10元,每人每天可栽植3棵树.要求初高中均有学生参加,且参加活动的初中学生比参加活动的高中学生多4人,本次活动的往返车费总和不得超过210元.要使本次活动植树最多,初高中各有多少学生参加?最多植树多少棵?
校区的每位初中学生往返车费是10元,每人每天可栽植3棵树.要求初高中均有学生参加,且参加活动的初中学生比参加活动的高中学生多4人,本次活动的往返车费总和不得超过210元.要使本次活动植树最多,初高中各有多少学生参加?最多植树多少棵?
 校区,初中部在
校区,初中部在 校区,学校学生会计划在3月12日植树节当天安排部分学生到郊区公园参加植树活动.已知
校区,学校学生会计划在3月12日植树节当天安排部分学生到郊区公园参加植树活动.已知 校区的每位高中学生往返车费是6元,每人每天可栽植5棵树;
校区的每位高中学生往返车费是6元,每人每天可栽植5棵树; 校区的每位初中学生往返车费是10元,每人每天可栽植3棵树.要求初高中均有学生参加,且参加活动的初中学生比参加活动的高中学生多4人,本次活动的往返车费总和不得超过210元.要使本次活动植树最多,初高中各有多少学生参加?最多植树多少棵?
校区的每位初中学生往返车费是10元,每人每天可栽植3棵树.要求初高中均有学生参加,且参加活动的初中学生比参加活动的高中学生多4人,本次活动的往返车费总和不得超过210元.要使本次活动植树最多,初高中各有多少学生参加?最多植树多少棵?21.路边路灯的灯柱 垂直于地面,灯杆
垂直于地面,灯杆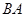 的长为2米,灯杆与灯柱
的长为2米,灯杆与灯柱 成
成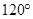 角,锥形灯罩的轴线
角,锥形灯罩的轴线 与灯杆
与灯杆 垂直,且灯罩轴线
垂直,且灯罩轴线 正好通过道路路面的中心线(
正好通过道路路面的中心线( 在中心线上).已知点
在中心线上).已知点 与点
与点 之间的距离为12米,求灯柱
之间的距离为12米,求灯柱 的高.(结果保留根号)
的高.(结果保留根号)
 垂直于地面,灯杆
垂直于地面,灯杆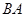 的长为2米,灯杆与灯柱
的长为2米,灯杆与灯柱 成
成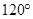 角,锥形灯罩的轴线
角,锥形灯罩的轴线 与灯杆
与灯杆 垂直,且灯罩轴线
垂直,且灯罩轴线 正好通过道路路面的中心线(
正好通过道路路面的中心线( 在中心线上).已知点
在中心线上).已知点 与点
与点 之间的距离为12米,求灯柱
之间的距离为12米,求灯柱 的高.(结果保留根号)
的高.(结果保留根号)
22.学校计划用地面砖铺设教学楼前矩形广场的地面 已知矩形广场地面的长为100米,宽为80米.图案设计如图所示:广场的四角为小正方形,阴影部分为四个矩形,四个矩形的宽都为小正方形的边长,阴影部分铺绿色地面砖,其余部分铺白色地面砖.
已知矩形广场地面的长为100米,宽为80米.图案设计如图所示:广场的四角为小正方形,阴影部分为四个矩形,四个矩形的宽都为小正方形的边长,阴影部分铺绿色地面砖,其余部分铺白色地面砖.

(1)要使铺白色地面砖的面积为5200平方米,那么矩形广场四角的小正方形的边长为多少米?
(2)如果铺白色地面砖的费用为每平方米30元,铺绿色地面砖的费用为每平方米20元.当广场四角小正方形的边长为多少米时,铺广场地面的总费用最少?最少费用是多少?
 已知矩形广场地面的长为100米,宽为80米.图案设计如图所示:广场的四角为小正方形,阴影部分为四个矩形,四个矩形的宽都为小正方形的边长,阴影部分铺绿色地面砖,其余部分铺白色地面砖.
已知矩形广场地面的长为100米,宽为80米.图案设计如图所示:广场的四角为小正方形,阴影部分为四个矩形,四个矩形的宽都为小正方形的边长,阴影部分铺绿色地面砖,其余部分铺白色地面砖.
(1)要使铺白色地面砖的面积为5200平方米,那么矩形广场四角的小正方形的边长为多少米?
(2)如果铺白色地面砖的费用为每平方米30元,铺绿色地面砖的费用为每平方米20元.当广场四角小正方形的边长为多少米时,铺广场地面的总费用最少?最少费用是多少?
23.如图,已知正方形 在直角坐标系
在直角坐标系 中,点
中,点 分别在
分别在 轴、
轴、 轴的正半轴上,点
轴的正半轴上,点 在坐标原点.等腰直角三角板
在坐标原点.等腰直角三角板 的直角顶点
的直角顶点 在原点,
在原点, 分别在
分别在 上,且
上,且 将三角板
将三角板 绕
绕 点逆时针旋转至
点逆时针旋转至 的位置,连结
的位置,连结

(1)求证:
(2)若三角板 绕
绕 点逆时针旋转一周,是否存在某一位置,使得
点逆时针旋转一周,是否存在某一位置,使得 若存在,请求出此时
若存在,请求出此时 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.
 在直角坐标系
在直角坐标系 中,点
中,点 分别在
分别在 轴、
轴、 轴的正半轴上,点
轴的正半轴上,点 在坐标原点.等腰直角三角板
在坐标原点.等腰直角三角板 的直角顶点
的直角顶点 在原点,
在原点, 分别在
分别在 上,且
上,且 将三角板
将三角板 绕
绕 点逆时针旋转至
点逆时针旋转至 的位置,连结
的位置,连结

(1)求证:

(2)若三角板
 绕
绕 点逆时针旋转一周,是否存在某一位置,使得
点逆时针旋转一周,是否存在某一位置,使得 若存在,请求出此时
若存在,请求出此时 点的坐标;若不存在,请说明理由.
点的坐标;若不存在,请说明理由.24.如图所示,抛物线与 轴交于点
轴交于点 两点,与
两点,与 轴交于点
轴交于点 以
以 为直径作
为直径作 过抛物线上一点
过抛物线上一点 作
作 的切线
的切线 切点为
切点为 并与
并与 的切线
的切线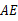 相交于点
相交于点 连结
连结 并延长交
并延长交 于点
于点 连结
连结

(1)求抛物线所对应的函数关系式及抛物线的顶点坐标;
(2)若四边形 的面积为
的面积为 求直线
求直线 的函数关系式;
的函数关系式;
(3)抛物线上是否存在点 ,使得四边形
,使得四边形 的面积等于
的面积等于 的面积?若存在,求出点
的面积?若存在,求出点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
 轴交于点
轴交于点 两点,与
两点,与 轴交于点
轴交于点 以
以 为直径作
为直径作 过抛物线上一点
过抛物线上一点 作
作 的切线
的切线 切点为
切点为 并与
并与 的切线
的切线 相交于点
相交于点 连结
连结 并延长交
并延长交 于点
于点 连结
连结

(1)求抛物线所对应的函数关系式及抛物线的顶点坐标;
(2)若四边形
 的面积为
的面积为 求直线
求直线 的函数关系式;
的函数关系式;(3)抛物线上是否存在点
 ,使得四边形
,使得四边形 的面积等于
的面积等于 的面积?若存在,求出点
的面积?若存在,求出点 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由. 搜索
搜索
 难度系数:0.65
难度系数:0.65  答案解析
答案解析
 有奖纠错
有奖纠错
