全一卷
1.-3的相反数是( )
| A.-3 | B.3 | C.±3 | D. |
2.下列计算错误的是
A. | B.(a2)3=a5 | C.2x2+3x2=5x2 | D. |
3.如图所示的是三通管的立体图,则这个几何体的俯视图是( )


A. | B. | C. | D. |
4.以下问题,不适合用全面调查的是( )
| A.了解全班同学每周体育锻炼的时间 | B.旅客上飞机前的安检 |
| C.学校招聘教师,对应聘人员面试 | D.了解全市中小学生每天的零花钱 |
5.已知反比例函数 的图象经过点(2,-2),则k的值为
的图象经过点(2,-2),则k的值为
 的图象经过点(2,-2),则k的值为
的图象经过点(2,-2),则k的值为| A.4 | B.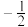 | C.-4 | D.-2 |
6.下列图案由正多边形拼成,其中既是轴对称图形又是中心对称图形的是( )
A. | B. | C. | D. |
7.将点A(3,2)沿x轴向左平移4个单位长度得到点A′,点A′关于y轴对称的点的坐标是( )
| A.(﹣3,2) | B.(﹣1,2) | C.(1,2) | D.(1,﹣2) |
8.用半径为3cm,圆心角是120°的扇形围成一个圆锥的侧面,则这个圆锥的底面半径为( )
A. | B.1.5cm | C. | D.1cm |
9.一个不透明的口袋里有4张形状完全相同的卡片,分别写有数字1,2,3,4,口袋外有两张卡片,分别写有数字2,3,现随机从口袋里取出一张卡片,求这张卡片与口袋外的两张卡片上的数能构成三角形的概率是
A. | B. | C. | D.1 |
10.如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于 MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法中正确的个数是
MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法中正确的个数是
①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;④S△DAC:S△ABC=1:3.

 MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法中正确的个数是
MN的长为半径画弧,两弧交于点P,连接AP并延长交BC于点D,则下列说法中正确的个数是①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的中垂线上;④S△DAC:S△ABC=1:3.

| A.1 | B.2 | C.3 | D.4 |
11.我国南海海域的面积约为3600000km2,该面积用科学记数法应表示为___ km2.
12.如图,有一块含有60°角的直角三角板的两个顶点放在矩形的对边上.如果∠1=18°,那么∠2的度数是 .


13.若一个多边形内角和等于1260°,则该多边形边数是______ .
14.如图,△ABC的三个顶点都在5×5的网格(每个小正方形的边长均为1个单位长度)的格点上,将△ABC绕点B逆时针旋转到△A′BC′的位置,且点A′、C′仍落在格点上,则图中阴影部分的面积约是___ .(π≈3.14,结果精确到0.1)


15.为庆祝“六一”儿童节,某幼儿园举行用火柴棒摆“金鱼”比赛.如图所示,按照这样的规律,摆第n个图,需用火柴棒的根数为_______________ .

16.计算: .
.
 .
.17.先化简,再求值: ,其中
,其中 .
.
 ,其中
,其中 .
.18.解不等式组: 并把它的解集在数轴上表示出来.
并把它的解集在数轴上表示出来.

 并把它的解集在数轴上表示出来.
并把它的解集在数轴上表示出来.
19.如图,已知四边形ABCD是平行四边形,DE⊥AB,DF⊥BC,垂足分别是E、F,并且DE=DF,求证:

(1)△ADE≌△CDF;
(2)四边形ABCD是菱形.

(1)△ADE≌△CDF;
(2)四边形ABCD是菱形.
20.一方有难,八方相助,2013年4月20日,四川省雅安市芦山县发生了里氏7.0级强烈地震.某厂接到在规定时间内加工1500顶帐篷支援灾区人民的任务.在加工了300顶帐篷后,厂家把工作效率提高到原来的1.5倍,于是提前4天完成任务,求原来每天加工多少顶帐篷?
21.钓鱼岛自古以来就是我国的神圣领土,为维护国家主权和海洋权利,我国海监和渔政部门对钓鱼岛海域实现了常态化巡航管理.如图,某日在我国钓鱼岛附近海域有两艘自西向东航行的海监船A、B,B船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,B的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少.(结果保留根号)


22.我市某中学举行“中国梦•校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

(1)根据图示填写下表;
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.

(1)根据图示填写下表;
| 平均数(分) | 中位数(分) | 众数(分) | |
| 初中部 | 85 | ||
| 高中部 | 85 | 100 |
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
23.四川省第十二届运动会将于2014年8月18日在我市隆重开幕,根据大会组委会安排,某校接受了开幕式大型团体操表演任务.为此,学校需要采购一批演出服装,A、B两家制衣公司都愿成为这批服装的供应商.经了解:两家公司生产的这款演出服装的质量和单价都相同,即男装每套120元,女装每套100元.经洽谈协商:A公司给出的优惠条件是,全部服装按单价打七折,但校方需承担2200元的运费;B公司的优惠条件是男女装均按每套100元打八折,公司承担运费.另外根据大会组委会要求,参加演出的女生人数应是男生人数的2倍少100人,如果设参加演出的男生有x人.
(1)分别写出学校购买A、B两公司服装所付的总费用y1(元)和y2(元)与参演男生人数x之间的函数关系式;
(2)问:该学校购买哪家制衣公司的服装比较合算?请说明理由.
(1)分别写出学校购买A、B两公司服装所付的总费用y1(元)和y2(元)与参演男生人数x之间的函数关系式;
(2)问:该学校购买哪家制衣公司的服装比较合算?请说明理由.
24.如图,在 中,直径
中,直径 ,垂足为E,点M在
,垂足为E,点M在 上,
上, 的延长线交⊙O于点G,交过C的直线于F,
的延长线交⊙O于点G,交过C的直线于F, ,连结
,连结 与
与 交于点N.
交于点N.

(1)求证: 是
是 的切线;
的切线;
(2)求证: ;
;
(3)若点M是 的中点,
的中点, 的半径为4,
的半径为4, ,求
,求 的长.
的长.
 中,直径
中,直径 ,垂足为E,点M在
,垂足为E,点M在 上,
上, 的延长线交⊙O于点G,交过C的直线于F,
的延长线交⊙O于点G,交过C的直线于F, ,连结
,连结 与
与 交于点N.
交于点N.
(1)求证:
 是
是 的切线;
的切线;(2)求证:
 ;
;(3)若点M是
 的中点,
的中点, 的半径为4,
的半径为4, ,求
,求 的长.
的长.25.如图,抛物线 与x轴交于点A(2,0),交y轴于点B(0,
与x轴交于点A(2,0),交y轴于点B(0,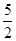 ).直线
).直线 过点A与y轴交于点C,与抛物线的另一个交点是D.
过点A与y轴交于点C,与抛物线的另一个交点是D.

(1)求抛物线 与直线
与直线 的解析式;
的解析式;
(2)设点P是直线AD上方的抛物线上一动点(不与点A、D重合),过点P作 y轴的平行线,交直线AD于点M,作DE⊥y轴于点E.探究:是否存在这样的点P,使四边形PMEC是平行四边形?若存在请求出点P的坐标;若不存在,请说明理由;
(3)在(2)的条件下,作PN⊥AD于点N,设△PMN的周长为l,点P的横坐标为x,求l与x的函数关系式,并求出l的最大值.
 与x轴交于点A(2,0),交y轴于点B(0,
与x轴交于点A(2,0),交y轴于点B(0,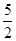 ).直线
).直线 过点A与y轴交于点C,与抛物线的另一个交点是D.
过点A与y轴交于点C,与抛物线的另一个交点是D.
(1)求抛物线
 与直线
与直线 的解析式;
的解析式;(2)设点P是直线AD上方的抛物线上一动点(不与点A、D重合),过点P作 y轴的平行线,交直线AD于点M,作DE⊥y轴于点E.探究:是否存在这样的点P,使四边形PMEC是平行四边形?若存在请求出点P的坐标;若不存在,请说明理由;
(3)在(2)的条件下,作PN⊥AD于点N,设△PMN的周长为l,点P的横坐标为x,求l与x的函数关系式,并求出l的最大值.
 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
