全一卷
1. 的绝对值是( ).
的绝对值是( ).
 的绝对值是( ).
的绝对值是( ).A. | B.2 | C. | D. |
2.如图,直线AB、CD被直线EF所截,则∠3的同旁内角是( ).

A.∠1 B.∠2 C.∠4 D.∠5

A.∠1 B.∠2 C.∠4 D.∠5
3.如图所示几何体的左视图是().
A. | B. | C. | D. |
4.下列运算正确的是( ).
A.  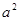 = = | B. | C. | D. |
5.如图,已知△ADE与△ABC的相似比为1:2,则△ADE与△ABC的面积比为( )


| A.1:2 | B.1:4 | C.2:1 | D.4:1 |
6.若反比例函数 的图象经过点(-3,2),则
的图象经过点(-3,2),则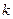 的值为( ).
的值为( ).
 的图象经过点(-3,2),则
的图象经过点(-3,2),则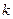 的值为( ).
的值为( ).| A.-6 | B.6 | C.-5 | D.5 |
7.下列说法正确的是( ).
| A.买一张福利彩票一定中奖,是必然事件. |
| B.买一张福利彩票一定中奖,是不可能事件. |
C.抛掷一个正方体骰子,点数为奇数的概率是 . . |
| D.一组数据:1,7,3,5,3的众数是3. |
8.一个圆锥的侧面展开图是半径为1的半圆,则该圆锥的底面半径是( ).


A. | B. | C. | D. |
9.将抛物线 绕它的顶点旋转180°,所得抛物线的解析式是()
绕它的顶点旋转180°,所得抛物线的解析式是()
 绕它的顶点旋转180°,所得抛物线的解析式是()
绕它的顶点旋转180°,所得抛物线的解析式是()A. | B. |
C. | D. |
10.如图,已知正方形ABCD的边长为4 ,E是BC边上的一个动点,AE⊥EF, EF交DC于F, 设BE= ,FC=
,FC= ,则当点E从点B运动到点C时,
,则当点E从点B运动到点C时, 关于
关于 的函数图象是( )
的函数图象是( )

 ,FC=
,FC= ,则当点E从点B运动到点C时,
,则当点E从点B运动到点C时, 关于
关于 的函数图象是( )
的函数图象是( )
A. | B. | C. | D. |
11.因式分解: =" " .
=" " .
 =" " .
=" " .12.情系玉树大爱无疆,截至5月21日12时,青海玉树共接收国内外地震救灾捐赠款物551300万元,将551300万元用科学记数法表示为__________万元.
13.函数 的自变量
的自变量 的取值范围是 .
的取值范围是 .
 的自变量
的自变量 的取值范围是 .
的取值范围是 .14.正五边形的内角和等于______度.
15.已知 ,则代数式
,则代数式 的值为_________.
的值为_________.
 ,则代数式
,则代数式 的值为_________.
的值为_________.16.如图:已知AB=10,点C、D在线段AB上且AC=DB=2; P是线段CD上的动点,分别以AP、PB为边在线段AB的同侧作等边△AEP和等边△PFB,连结EF,设EF的中点为G;当点P从点C运动到点D时,则点G移动路径的长是________.

17.(本题满分6分)计算: 4cos30°+
4cos30°+
 4cos30°+
4cos30°+
18.(本题满分6分)
先化简,再求值: ,其中
,其中
先化简,再求值:
 ,其中
,其中
19.(本题满分8分) 求证:矩形的对角线相等.
20.(本题满分8分)
如图是某地6月1日至6月7日每天最高、最低气温的折线统计图.

请你根据折线统计图,回答下列问题:
(1)在这7天中,日温差最大的一天是6月_____日;
(2)这7天的日最高气温的平均数是______℃;
 (3)这7天日最高气温的方差是 _______ .
(3)这7天日最高气温的方差是 _______ .
如图是某地6月1日至6月7日每天最高、最低气温的折线统计图.

请你根据折线统计图,回答下列问题:
(1)在这7天中,日温差最大的一天是6月_____日;
(2)这7天的日最高气温的平均数是______℃;
 (3)这7天日最高气温的方差是 _______ .
(3)这7天日最高气温的方差是 _______ . 21.(本题满分8分)
某蔬菜公司收购到某种蔬菜104吨,准备加工后上市销售. 该公司加工该种蔬菜的能力是:每天可以精加工4吨或粗加工8吨. 现计划用16天正好完成加工任务,则该公司应安排几天精加工,几天粗加工?
某蔬菜公司收购到某种蔬菜104吨,准备加工后上市销售. 该公司加工该种蔬菜的能力是:每天可以精加工4吨或粗加工8吨. 现计划用16天正好完成加工任务,则该公司应安排几天精加工,几天粗加工?
22.
某校初三年级春游,现有36座和42座两种客车供选择租用,若只租用36座客车若干辆,则正好坐满;若只租用42座客车,则能少租一辆,且有一辆车没有坐满,但超过30人;已知36座客车每辆租金400元,42座客车每辆租金440元.
(1)该校初三年级共有多少人参加春游?
(2)请你帮该校设计一种最省钱的租车方案.
某校初三年级春游,现有36座和42座两种客车供选择租用,若只租用36座客车若干辆,则正好坐满;若只租用42座客车,则能少租一辆,且有一辆车没有坐满,但超过30人;已知36座客车每辆租金400元,42座客车每辆租金440元.
(1)该校初三年级共有多少人参加春游?
(2)请你帮该校设计一种最省钱的租车方案.
23.(本题满分10分)如图,⊙O是△ABC的外接圆,FH是⊙O 的切线,切点为F,
FH∥BC,连结AF交BC于E,∠ABC的平分线BD交AF于D,连结BF.

(1)证明:AF平分∠BAC;
(2)证明:BF=FD;
(3)若EF=4,DE=3,求AD的长.
FH∥BC,连结AF交BC于E,∠ABC的平分线BD交AF于D,连结BF.

(1)证明:AF平分∠BAC;
(2)证明:BF=FD;
(3)若EF=4,DE=3,求AD的长.
24.(本题满分12分)
如图,过A(8,0)、B(0, )两点的直线与直线
)两点的直线与直线 交于点C.平行于
交于点C.平行于 轴的直线
轴的直线 从原点O出发,以每秒1个单位长度的速度沿
从原点O出发,以每秒1个单位长度的速度沿 轴向右平移,到C点时停止;
轴向右平移,到C点时停止; 分别交线段BC、OC于点D、E,以DE为边向左侧作等边△
分别交线段BC、OC于点D、E,以DE为边向左侧作等边△ DEF,设△DEF与△BCO重叠部分的面积为S(平方单位),直线
DEF,设△DEF与△BCO重叠部分的面积为S(平方单位),直线 的运动时间为t(
的运动时间为t( 秒).
秒).

(1)直接写出C点坐标和t的取值范围;
(2)求S与t的函数关系式;
(3)设直线 与
与 轴交于点P,是否存在这样的点P,使得以P、O、F为顶点的三角形为等腰三角形,若存在,请直接写出点P的坐标;若不存在,请说明理由.
轴交于点P,是否存在这样的点P,使得以P、O、F为顶点的三角形为等腰三角形,若存在,请直接写出点P的坐标;若不存在,请说明理由.
如图,过A(8,0)、B(0,
 )两点的直线与直线
)两点的直线与直线 交于点C.平行于
交于点C.平行于 轴的直线
轴的直线 从原点O出发,以每秒1个单位长度的速度沿
从原点O出发,以每秒1个单位长度的速度沿 轴向右平移,到C点时停止;
轴向右平移,到C点时停止; 分别交线段BC、OC于点D、E,以DE为边向左侧作等边△
分别交线段BC、OC于点D、E,以DE为边向左侧作等边△ DEF,设△DEF与△BCO重叠部分的面积为S(平方单位),直线
DEF,设△DEF与△BCO重叠部分的面积为S(平方单位),直线 的运动时间为t(
的运动时间为t( 秒).
秒).
(1)直接写出C点坐标和t的取值范围;
(2)求S与t的函数关系式;
(3)设直线
 与
与 轴交于点P,是否存在这样的点P,使得以P、O、F为顶点的三角形为等腰三角形,若存在,请直接写出点P的坐标;若不存在,请说明理由.
轴交于点P,是否存在这样的点P,使得以P、O、F为顶点的三角形为等腰三角形,若存在,请直接写出点P的坐标;若不存在,请说明理由.25. 的算术平方根是:
的算术平方根是:
 的算术平方根是:
的算术平方根是:| A.4 | B. | C. | D. |
26.下列计算正确的是:
A. | B. | C. | D. |
27.用4个棱长为1的正方体搭成一个几何体模型,其主视图与左视图如图4所示,则该立方体的俯视图不可能是:




28.不等式组 的解集是:
的解集是:
 的解集是:
的解集是:A. | B. | C. | D. |
29.
某品牌商品,按标价九折出售,仍可获得20%的利润.若该商品标价为28元,则商品的进价为:
某品牌商品,按标价九折出售,仍可获得20%的利润.若该商品标价为28元,则商品的进价为:
| A.21元 | B.19.8元 | C. 22.4元 | D.25.2元 |
30.如图,EF是△ABC的中位线,将△AEF沿中线AD方向平移到△A E
E F
F 的位置,使E
的位置,使E F
F 与BC边重合,已知△AEF的面积为7,则图中阴影部分的面积为:
与BC边重合,已知△AEF的面积为7,则图中阴影部分的面积为:

 E
E F
F 的位置,使E
的位置,使E F
F 与BC边重合,已知△AEF的面积为7,则图中阴影部分的面积为:
与BC边重合,已知△AEF的面积为7,则图中阴影部分的面积为:
| A.7 | B.14 | C.21 | D.28 |
31.某班随机抽取6名同学的一次地生测试成绩如下:82,95,82,76,76,82.数据中的众数和中位数分别是:
| A.82,76 | B.76,82 | C.82,79 | D.82,82 |
32.如图6, 已知圆锥的高为8,底面圆的直径为12,则此圆锥的侧面积是


A.24 | B.30 | C.48 | D.60 |
33.9的相反数是 .
34.据有关部门预测,恩施州煤炭总储量为2.91亿吨,用科学记数法表示这个数是
吨(保留两个有效数字).
吨(保留两个有效数字).
35.分解因式: .
.
 .
.36.在一个不透明的盒子里装有5个黑球,3个红球和2个白球,它们除颜色外其余都相同,从中随机摸出一个球,摸到红球的概率是 .
37.在同一直角坐标系中,正比例函数 的图象与反比例函数
的图象与反比例函数 的图象有公共点,则
的图象有公共点,则 0(填“>”、“=”或“<”).
0(填“>”、“=”或“<”).
 的图象与反比例函数
的图象与反比例函数 的图象有公共点,则
的图象有公共点,则 0(填“>”、“=”或“<”).
0(填“>”、“=”或“<”).38.如图,在 ABCD中,已知AB=9㎝,AD=6㎝,BE平分∠ABC交DC边于点E,则DE等于 ㎝.
ABCD中,已知AB=9㎝,AD=6㎝,BE平分∠ABC交DC边于点E,则DE等于 ㎝.
 ABCD中,已知AB=9㎝,AD=6㎝,BE平分∠ABC交DC边于点E,则DE等于 ㎝.
ABCD中,已知AB=9㎝,AD=6㎝,BE平分∠ABC交DC边于点E,则DE等于 ㎝.
39.如图,在矩形ABCD中,AD =4,DC =3,将△ADC按逆时针方向绕点A旋转到△AEF(点A、B、E在同一直线上),连结CF,则CF =_____ .


40.如图,有一个形如六边形的点阵,它的中心是一个点,作为第一层,第二层每边有两个点,第三层每边有三个点,依次类推,如果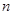 层六边形点阵的总点数为331,则
层六边形点阵的总点数为331,则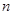 等于 .
等于 .
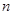 层六边形点阵的总点数为331,则
层六边形点阵的总点数为331,则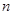 等于 .
等于 .
41.(6分) 计算:2+ -
-
 -
-
42.(8分)解方程:

43.如图7,已知,在 ABCD中,AE=CF,M、N分别是DE、BF的中点.
ABCD中,AE=CF,M、N分别是DE、BF的中点.

求证:四边形MFNE是平行四边形 .
 ABCD中,AE=CF,M、N分别是DE、BF的中点.
ABCD中,AE=CF,M、N分别是DE、BF的中点.
求证:四边形MFNE是平行四边形 .
44.(8分)2010年4月14日青海玉树发生7.1级地震,地震灾情牵动全国人民的心.某社区响应恩施州政府的号召,积极组织社区居民为灾区人民献爱心活动.为了解该社区居民捐款情况,对社区部分捐款户数进行分组统计(统计表如下),数据整理成如图8所示的不完整统计图.已知A、B两组捐款户数直方图的高度比为1:5,请结合图中相关数据回答下列问题.


⑴ A组的频数是多少?本次调查样本的容量是多少?
⑵ 求出C组的频数并补全直方图.
⑶ 若该社区有500户住户,请估计捐款不少于300元的户数是多少?


⑴ A组的频数是多少?本次调查样本的容量是多少?
⑵ 求出C组的频数并补全直方图.
⑶ 若该社区有500户住户,请估计捐款不少于300元的户数是多少?
45.(10分) 如图9,已知,在△ABC中,∠ABC= ,BC为⊙O的直径, AC与⊙O交于点D,点E为AB的中点,PF⊥BC交BC于点G,交AC于点F.
,BC为⊙O的直径, AC与⊙O交于点D,点E为AB的中点,PF⊥BC交BC于点G,交AC于点F.

(1)求证:ED是⊙O的切线.
(2)如果CF ="1,CP" =2,sinA = ,求⊙O的直径BC.
,求⊙O的直径BC.
 ,BC为⊙O的直径, AC与⊙O交于点D,点E为AB的中点,PF⊥BC交BC于点G,交AC于点F.
,BC为⊙O的直径, AC与⊙O交于点D,点E为AB的中点,PF⊥BC交BC于点G,交AC于点F.
(1)求证:ED是⊙O的切线.
(2)如果CF ="1,CP" =2,sinA =
 ,求⊙O的直径BC.
,求⊙O的直径BC.46.(10分) 恩施州绿色、富硒产品和特色农产品在国际市场上颇具竞争力,其中香菇远销日本和韩国等地.上市时,外商李经理按市场价格10元/千克在我州收购了2000千克香菇存放入冷库中.据预测,香菇的市场价格每天每千克将上涨0.5元,但冷库存放这批香菇时每天需要支出各种费用合计340元,而且香菇在冷库中最多保存110天,同时,平均每天有6千克的香菇损坏不能出售.
(1)若存放 天后,将这批香菇一次性出售,设这批香菇的销售总金额为
天后,将这批香菇一次性出售,设这批香菇的销售总金额为 元,试写出
元,试写出 与
与 之间的函数关系式.
之间的函数关系式.
(2)李经理想获得利润22500元,需将这批香菇存放多少天后出售?(利润=销售总金额-收购成本-各种费用)
(3)李经理将这批香菇存放多少天后出售可获得最大利润?最大利润是多少?
(1)若存放
 天后,将这批香菇一次性出售,设这批香菇的销售总金额为
天后,将这批香菇一次性出售,设这批香菇的销售总金额为 元,试写出
元,试写出 与
与 之间的函数关系式.
之间的函数关系式.(2)李经理想获得利润22500元,需将这批香菇存放多少天后出售?(利润=销售总金额-收购成本-各种费用)
(3)李经理将这批香菇存放多少天后出售可获得最大利润?最大利润是多少?
47.(10分)
(1)计算:如图10①,直径为 的三等圆⊙O
的三等圆⊙O 、⊙O
、⊙O 、⊙O
、⊙O 两两外切,切点分别为A、B、C ,求O
两两外切,切点分别为A、B、C ,求O A的长(用含
A的长(用含 的代数式表示).
的代数式表示).

(2)探索:若干个直径为 的圆圈分别按如图10②所示的方案一和如图10③所示的方案二的方式排放,探索并求出这两种方案中
的圆圈分别按如图10②所示的方案一和如图10③所示的方案二的方式排放,探索并求出这两种方案中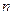 层圆圈的高度
层圆圈的高度 和
和 (用含
(用含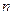 、
、 的代数式表示).
的代数式表示).
(3)应用:现有长方体集装箱,其内空长为5米,宽为3.1米,高为3.1米.用这样的集装箱装运长为5米,底面直径(横截面的外圆直径)为0.1米的圆柱形钢管,你认为采用(2)中的哪种方案在该集装箱中装运钢管数最多?并求出一个这样的集装箱最多能装运多少根钢管?( ≈1.73)
≈1.73)
(1)计算:如图10①,直径为
 的三等圆⊙O
的三等圆⊙O 、⊙O
、⊙O 、⊙O
、⊙O 两两外切,切点分别为A、B、C ,求O
两两外切,切点分别为A、B、C ,求O A的长(用含
A的长(用含 的代数式表示).
的代数式表示).
|
|
|
|
 的圆圈分别按如图10②所示的方案一和如图10③所示的方案二的方式排放,探索并求出这两种方案中
的圆圈分别按如图10②所示的方案一和如图10③所示的方案二的方式排放,探索并求出这两种方案中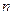 层圆圈的高度
层圆圈的高度 和
和 (用含
(用含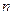 、
、 的代数式表示).
的代数式表示).(3)应用:现有长方体集装箱,其内空长为5米,宽为3.1米,高为3.1米.用这样的集装箱装运长为5米,底面直径(横截面的外圆直径)为0.1米的圆柱形钢管,你认为采用(2)中的哪种方案在该集装箱中装运钢管数最多?并求出一个这样的集装箱最多能装运多少根钢管?(
 ≈1.73)
≈1.73)48.如图,在平面直角坐标系中,二次函数 的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,-3),点P是直线BC下方抛物线上的一个动点.
的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,-3),点P是直线BC下方抛物线上的一个动点.

(1)求二次函数解析式;
(2)连接PO,PC,并将△POC沿y轴对折,得到四边形 .是否存在点P,使四边形
.是否存在点P,使四边形 为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由;
为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由;
(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.
 的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,-3),点P是直线BC下方抛物线上的一个动点.
的图象与x轴交于A、B两点,B点的坐标为(3,0),与y轴交于点C(0,-3),点P是直线BC下方抛物线上的一个动点.
(1)求二次函数解析式;
(2)连接PO,PC,并将△POC沿y轴对折,得到四边形
 .是否存在点P,使四边形
.是否存在点P,使四边形 为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由;
为菱形?若存在,求出此时点P的坐标;若不存在,请说明理由;(3)当点P运动到什么位置时,四边形ABPC的面积最大?求出此时P点的坐标和四边形ABPC的最大面积.
 搜索
搜索
 难度系数:0.64
难度系数:0.64  答案解析
答案解析
 有奖纠错
有奖纠错
 ②
②