搜索
全一卷
难度系数：0.85 
答案解析
有奖纠错
1．下列空间图形中是圆柱的为（ ）
A． | B． | C． | D． |
2．如图所示的两圆位置关系是（）
| A．相离 | B．外切 | C．相交 | D．内切 |
3．函数
是（）
是（）| A．一次函数 | B．二次函数 | C．正比例函数 | D．反比例函数 |
4．一只小狗正在平面镜前欣赏自己的全身像（如图所示），此时，它所看到的全身像是( )
A． | B． | C． | D． |
5．如图，半径为1的圆中，圆心角为120°的扇形面积为（）
A． | B． | C． | D． |
6．下列关于
的一元二次方程中，有两个不相等的实数根的方程是（）
的一元二次方程中，有两个不相等的实数根的方程是（）A． | B． |
C． | D． |
7．阻值为
和
的两个电阻，其两端电压
关于电流强度
的函数图象如图，则阻值（）
和
的两个电阻，其两端电压
关于电流强度
的函数图象如图，则阻值（）
| A．＞ | B．＜ | C．＝ | D．以上均有可能 |
8．不等式组
的解集在数轴上可以表示为（）
的解集在数轴上可以表示为（）A． | B． | C． | D． |
9．若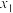
、
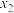是一元二次方程
的两根，则
的值是（ ）
、
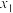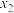是一元二次方程
的两根，则
的值是（ ）A． | B． | C． | D． |
10．某超市进了一批商品，每件进价为a元，若要获利25%，则每件商品的零售价应定为（）
A． | B． | C． | D． |
11．如图，已知：正方形ABCD边长为1，E、F、G、H分别为各边上的点，且AE=BF=CG=DH, 设小正方形EFGH的面积为
，AE为
，则关于的函数图象大致是（）
，AE为
，则关于的函数图象大致是（）
A． | B． | C． | D． |
12．如图，PA 、PB是⊙O的切线，A、 B 为切点，OP交AB于点D，交⊙O于点C , 在线段AB、PA、PB、PC、CD中，已知其中两条线段的长，但还无法计算出⊙O直径的两条线段是（ ）
| A．AB、CD | B．PA、PC | C．PA、AB | D．PA、PB |
13．
=_________
=14．如图，在这三张扑克牌中任意抽取一张，抽到“红桃7”的概率是 .
15．外接圆半径为
的正六边形周长为___________ ．
的正六边形周长为
16．试写出图象位于第二象限与第四象限的一个反比例函数解析式 .
17．如图，D、E为△ABC两边AB、AC的中点，将△ABC沿线段DE折叠，使点A落在点F处，若∠B=55°，则∠BDF=_______ °．
18．某种药品的说明书上，贴有如图所示的标签，一次服用这种药品的剂量范围是 mg～ mg
19．小舒家的水表如图所示，该水表的读数为______________ 
（精确到0.1）
（精确到0.1）
20．在计算器上按照下面的程序进行操作：
下表中的x与y分别是输入的6个数及相应的计算结果：
上面操作程序中所按的第三个键和第四个键应是
下表中的x与y分别是输入的6个数及相应的计算结果：
| x | -2 | -1 | 0 | 1 | 2 | 3 |
| y | -5 | -2 | 1 | 4 | 7 | 10 |
上面操作程序中所按的第三个键和第四个键应是
21．解方程：
22．如图，在4×4的正方形方格中，△ABC和△DEF的顶点都在边长为1的小正方形的顶点上.
（1）填空：∠ABC= °，BC= ；
（2）判断△ABC与△DEF是否相似，并证明你的结论.
（1）填空：∠ABC= °，BC= ；
（2）判断△ABC与△DEF是否相似，并证明你的结论.
23．现有7名同学测得某大厦的高度如下：（单位：
）29.8 30.0 30.0 30.0 30.2 44.0 30.0
(1) 在这组数据中,中位数是 ，众数是 ，平均数是 ；
(2) 凭经验，你觉得此大厦大概有多高?请简要说明理由.
）29.8 30.0 30.0 30.0 30.2 44.0 30.0
(1) 在这组数据中,中位数是 ，众数是 ，平均数是 ；
(2) 凭经验，你觉得此大厦大概有多高?请简要说明理由.
24．如图，我市某广场一灯柱AB被一钢缆CD固定，CD与地面成40°夹角，且DB=5m，则 BC的长度是多少？现再在C点上方2m处加固另一条钢缆ED，那么钢缆ED的长度为多少？（结果保留三个有效数字）
（参考数据：
）
（参考数据：
）
25．如图，用长为18 m的篱笆（虚线部分），两面靠墙围成矩形的苗圃.
（1）设矩形的一边为（m），面积为
(m2)，求关于的函数关系式，并写出自变量的取值范围；
（2）当为何值时，所围苗圃的面积最大，最大面积是多少？
（1）设矩形的一边为
（m），面积为
(m2)，求关于的函数关系式，并写出自变量的取值范围；（2）当
为何值时，所围苗圃的面积最大，最大面积是多少？26．我国古代数学家秦九韶在《数书九章》中记述了“三斜求积术”，
即已知三角形的三边长，求它的面积．用现代式子表示即为：
……①（其中
、
、
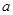为三角形的三边长，
为面积）.
而另一个文明古国古希腊也有求三角形面积的海伦公式：
……②（其中
）.
⑴ 若已知三角形的三边长分别为5、7、8，试分别运用公式①和公式②，计算该三角形的面积；
⑵ 你能否由公式①推导出公式②？请试试.
即已知三角形的三边长，求它的面积．用现代式子表示即为：
……①（其中
、
、
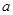为三角形的三边长，
为面积）.而另一个文明古国古希腊也有求三角形面积的海伦公式：
……②（其中
）.⑴ 若已知三角形的三边长分别为5、7、8，试分别运用公式①和公式②，计算该三角形的面积
；⑵ 你能否由公式①推导出公式②？请试试.
27．如图，在平面直角坐标系内，⊙C与y轴相切于D点，与x轴相交于A（2，0）、B（8，0）两点，圆心C在第四象限．
（1）求点C的坐标；
（2）连接BC并延长交⊙C于另一点E，若线段BE上有一点P，使得AB2=BP•BE，能否推出AP⊥BE？请给出你的结论，并说明理由；
（3）在直线BE上是否存在点Q，使得AQ2=BQ•EQ？若存在，求出点Q的坐标；若不存在，也请说明理由．
（1）求点C的坐标；
（2）连接BC并延长交⊙C于另一点E，若线段BE上有一点P，使得AB2=BP•BE，能否推出AP⊥BE？请给出你的结论，并说明理由；
（3）在直线BE上是否存在点Q，使得AQ2=BQ•EQ？若存在，求出点Q的坐标；若不存在，也请说明理由．
