全一卷
1.计算 的值是( )
的值是( )
 的值是( )
的值是( )A. | B. | C. | D.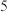 |
2.化简 的结果是( )
的结果是( )
 的结果是( )
的结果是( )A. | B. | C. | D. |
3.据《连云港日报》报道,至2008年5月1日零时,田湾核电站1、2号两台机组今年共累计发电42.96亿千瓦时.“42.96亿”用科学记数法可表示为()
A. | B. | C. | D. |
4.函数 的自变量x的取值范围是( )
的自变量x的取值范围是( )
 的自变量x的取值范围是( )
的自变量x的取值范围是( )A. | B. | C. | D. |
5.实数 在数轴上对应点的位置如图所示,则必有( )
在数轴上对应点的位置如图所示,则必有( )

 在数轴上对应点的位置如图所示,则必有( )
在数轴上对应点的位置如图所示,则必有( )
A. | B. | C. | D. |
6.若一个几何体的主视图、左视图、俯视图分别是三角形、三角形、圆,则这个几何体可能是( )
| A.球 | B.圆柱 | C.圆锥 | D.棱锥 |
7.已知 为矩形
为矩形 的对角线,则图中
的对角线,则图中 与
与 一定不相等的是( )
一定不相等的是( )
 为矩形
为矩形 的对角线,则图中
的对角线,则图中 与
与 一定不相等的是( )
一定不相等的是( )A. | B. | C. | D. |
8.已知某反比例函数的图象经过点 ,则它一定也经过点()
,则它一定也经过点()
 ,则它一定也经过点()
,则它一定也经过点()A. | B. | C. | D. |
9.如果 ,那么
,那么 的算术平方根是
的算术平方根是_________ .
 ,那么
,那么 的算术平方根是
的算术平方根是10.当 时,代数式
时,代数式 的值为 .
的值为 .
 时,代数式
时,代数式 的值为 .
的值为 .11.在 中,
中, ,
, ,
, ,则
,则 __________.
__________.
 中,
中, ,
, ,
, ,则
,则 __________.
__________.
12.若一个分式含有字母 ,且当
,且当 时,它的值为12,则这个分式可以是 .
时,它的值为12,则这个分式可以是 .
(写出一个即可)
 ,且当
,且当 时,它的值为12,则这个分式可以是 .
时,它的值为12,则这个分式可以是 .(写出一个即可)
13.不等式组 的解集是
的解集是____________ .
 的解集是
的解集是14.如图,一落地晾衣架两撑杆的公共点为 ,
, cm,
cm, cm.若撑杆下端点
cm.若撑杆下端点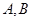 所在直线平行于上端点
所在直线平行于上端点 所在直线,且
所在直线,且 cm,则
cm,则
_____ cm.

 ,
, cm,
cm, cm.若撑杆下端点
cm.若撑杆下端点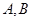 所在直线平行于上端点
所在直线平行于上端点 所在直线,且
所在直线,且 cm,则
cm,则

15.如图,扇形彩色纸的半径为45cm,圆心角为 ,用它制作一个圆锥形火炬模型的侧面(接头忽略不计),则这个圆锥的高约为
,用它制作一个圆锥形火炬模型的侧面(接头忽略不计),则这个圆锥的高约为____ cm.(结果精确到0.1cm.参考数据: ,
, ,
, ,
, )
)

 ,用它制作一个圆锥形火炬模型的侧面(接头忽略不计),则这个圆锥的高约为
,用它制作一个圆锥形火炬模型的侧面(接头忽略不计),则这个圆锥的高约为 ,
, ,
, ,
, )
)
16.如图所示,①中多边形(边数为12)是由正三角形“扩展”而来的,②中多边形是由正方形“扩展”而来的,…,依此类推,则由正n边形“扩展”而来的多边形的边数为__ .


17.计算: ;
;
 ;
;18.解方程:x2+4x﹣1=0.
19.如图, 内接于⊙O,
内接于⊙O, 为⊙O的直径,
为⊙O的直径, ,
, ,过点
,过点 作⊙O的切线与
作⊙O的切线与 的延长线交于点
的延长线交于点 ,求
,求 的长.
的长.
 内接于⊙O,
内接于⊙O, 为⊙O的直径,
为⊙O的直径, ,
, ,过点
,过点 作⊙O的切线与
作⊙O的切线与 的延长线交于点
的延长线交于点 ,求
,求 的长.
的长.
20.如图,在平面直角坐标系中,点 的坐标分别为
的坐标分别为 .
.
(1)请在图中画出 ,使得
,使得 与
与 关于点
关于点 成中心对称;
成中心对称;
(2)若一个二次函数的图象经过(1)中 的三个顶点,求此二次函数的关系式.
的三个顶点,求此二次函数的关系式.
 的坐标分别为
的坐标分别为 .
.(1)请在图中画出
 ,使得
,使得 与
与 关于点
关于点 成中心对称;
成中心对称;(2)若一个二次函数的图象经过(1)中
 的三个顶点,求此二次函数的关系式.
的三个顶点,求此二次函数的关系式.
21.如图,在直角梯形纸片 中,
中, ,
, ,
, ,将纸片沿过点
,将纸片沿过点 的直线折叠,使点
的直线折叠,使点 落在边
落在边 上的点
上的点 处,折痕为
处,折痕为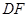 .连接
.连接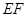 并展开纸片.
并展开纸片.
(1)求证:四边形 是正方形;
是正方形;
(2)取线段 的中点
的中点 ,连接
,连接 ,如果
,如果 ,试说明四边形
,试说明四边形 是等腰梯形.
是等腰梯形.
 中,
中, ,
, ,
, ,将纸片沿过点
,将纸片沿过点 的直线折叠,使点
的直线折叠,使点 落在边
落在边 上的点
上的点 处,折痕为
处,折痕为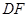 .连接
.连接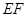 并展开纸片.
并展开纸片.(1)求证:四边形
 是正方形;
是正方形;(2)取线段
 的中点
的中点 ,连接
,连接 ,如果
,如果 ,试说明四边形
,试说明四边形 是等腰梯形.
是等腰梯形.
22.某中学为了了解七年级学生的课外阅读情况,随机调查了该年级的25名学生,得到了他们上周双休日课外阅读时间(记为 ,单位:小时)的一组样本数据,其扇形统计图如图所示,其中
,单位:小时)的一组样本数据,其扇形统计图如图所示,其中 表示与
表示与 对应的学生数占被调查人数的百分比.
对应的学生数占被调查人数的百分比.
(1)求与 相对应的
相对应的 值;
值;
(2)试确定这组样本数据的中位数和众数;
(3)请估计该校七年级学生上周双休日的平均课外阅读时间.
 ,单位:小时)的一组样本数据,其扇形统计图如图所示,其中
,单位:小时)的一组样本数据,其扇形统计图如图所示,其中 表示与
表示与 对应的学生数占被调查人数的百分比.
对应的学生数占被调查人数的百分比.(1)求与
 相对应的
相对应的 值;
值;(2)试确定这组样本数据的中位数和众数;
(3)请估计该校七年级学生上周双休日的平均课外阅读时间.

23.甲、乙两人玩“锤子、石头、剪子、布”游戏,他们在不透明的袋子中放入形状、大小均相同的15张卡片,其中写有“锤子”、“石头”、“剪子”、“布”的卡片张数分别为2,3,4,6.两人各随机摸出一张卡片(先摸者不放回)来比胜负,并约定:“锤子”胜“石头”和“剪子”,“石头”胜“剪子”,“剪子”胜“布”,“布”胜“锤子”和“石头”,同种卡片不分胜负.
(1)若甲先摸,则他摸出“石头”的概率是多少?
(2)若甲先摸出了“石头”,则乙获胜的概率是多少?
(3)若甲先摸,则他先摸出哪种卡片获胜的可能性最大?
(1)若甲先摸,则他摸出“石头”的概率是多少?
(2)若甲先摸出了“石头”,则乙获胜的概率是多少?
(3)若甲先摸,则他先摸出哪种卡片获胜的可能性最大?
24.“爱心”帐篷集团的总厂和分厂分别位于甲、乙两市,两厂原来每周生产帐篷共9千顶,现某地震灾区急需帐篷14千顶,该集团决定在一周内赶制出这批帐篷.为此,全体职工加班加点,总厂和分厂一周内制作的帐篷数分别达到了原来的1.6倍、1.5倍,恰好按时完成了这项任务.
(1)在赶制帐篷的一周内,总厂和分厂各生产帐篷多少千顶;
(2)现要将这些帐篷用卡车一次性运送到该地震灾区的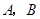 两地,由于两市通住
两地,由于两市通住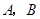 两地道路的路况不同,卡车的运载量也不同.已知运送帐篷每千顶所需的车辆数、两地所急需的帐篷数如下表:
两地道路的路况不同,卡车的运载量也不同.已知运送帐篷每千顶所需的车辆数、两地所急需的帐篷数如下表:
请设计一种运送方案,使所需的车辆总数最少.说明理由,并求出最少车辆总数.
(1)在赶制帐篷的一周内,总厂和分厂各生产帐篷多少千顶;
(2)现要将这些帐篷用卡车一次性运送到该地震灾区的
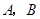 两地,由于两市通住
两地,由于两市通住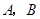 两地道路的路况不同,卡车的运载量也不同.已知运送帐篷每千顶所需的车辆数、两地所急需的帐篷数如下表:
两地道路的路况不同,卡车的运载量也不同.已知运送帐篷每千顶所需的车辆数、两地所急需的帐篷数如下表:| |  地 地 |  地 地 | |
| 每千顶帐篷 所需车辆数 | 甲市 | 4 | 7 |
| 乙市 | 3 | 5 | |
| 所急需帐篷数(单位:千顶) | 9 | 5 | |
请设计一种运送方案,使所需的车辆总数最少.说明理由,并求出最少车辆总数.
25.如图,现有两块全等的直角三角形纸板Ⅰ,Ⅱ,它们两直角边的长分别为1和2.将它们分别放置于平面直角坐标系中的 ,
, 处,直角边
处,直角边 在
在 轴上.一直尺从上方紧靠两纸板放置,让纸板Ⅰ沿直尺边缘平行移动.当纸板Ⅰ移动至
轴上.一直尺从上方紧靠两纸板放置,让纸板Ⅰ沿直尺边缘平行移动.当纸板Ⅰ移动至 处时,设
处时,设 与
与 分别交于点
分别交于点 ,与
,与 轴分别交于点
轴分别交于点 .
.
(1)求直线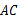 所对应的函数关系式;
所对应的函数关系式;
(2)当点 是线段
是线段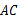 (端点除外)上的动点时,试探究:
(端点除外)上的动点时,试探究:
①点 到
到 轴的距离
轴的距离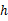 与线段
与线段 的长是否总相等?请说明理由;
的长是否总相等?请说明理由;
②两块纸板重叠部分(图中的阴影部分)的面积 是否存在最大值?若存在,求出这个最大值及
是否存在最大值?若存在,求出这个最大值及 取最大值时点
取最大值时点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
 ,
, 处,直角边
处,直角边 在
在 轴上.一直尺从上方紧靠两纸板放置,让纸板Ⅰ沿直尺边缘平行移动.当纸板Ⅰ移动至
轴上.一直尺从上方紧靠两纸板放置,让纸板Ⅰ沿直尺边缘平行移动.当纸板Ⅰ移动至 处时,设
处时,设 与
与 分别交于点
分别交于点 ,与
,与 轴分别交于点
轴分别交于点 .
.(1)求直线
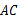 所对应的函数关系式;
所对应的函数关系式;(2)当点
 是线段
是线段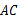 (端点除外)上的动点时,试探究:
(端点除外)上的动点时,试探究:①点
 到
到 轴的距离
轴的距离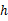 与线段
与线段 的长是否总相等?请说明理由;
的长是否总相等?请说明理由;②两块纸板重叠部分(图中的阴影部分)的面积
 是否存在最大值?若存在,求出这个最大值及
是否存在最大值?若存在,求出这个最大值及 取最大值时点
取最大值时点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
26.我们将能完全覆盖某平面图形的最小圆称为该平面图形的最小覆盖圆.例如线段 的最小覆盖圆就是以线段
的最小覆盖圆就是以线段 为直径的圆.
为直径的圆.
(1)请分别作出图1中两个三角形的最小覆盖圆(要求用尺规作图,保留作图痕迹,不写作法);

(2)探究三角形的最小覆盖圆有何规律?请写出你所得到的结论(不要求证明);
(3)某地有四个村庄 ,
, ,
, ,
, (其位置如图2所示),现拟建一个电视信号中转站,为了使这四个村庄的居民都能接收到电视信号,且使中转站所需发射功率最小(距离越小,所需功率越小),此中转站应建在何处?请说明理由.
(其位置如图2所示),现拟建一个电视信号中转站,为了使这四个村庄的居民都能接收到电视信号,且使中转站所需发射功率最小(距离越小,所需功率越小),此中转站应建在何处?请说明理由.

 的最小覆盖圆就是以线段
的最小覆盖圆就是以线段 为直径的圆.
为直径的圆.(1)请分别作出图1中两个三角形的最小覆盖圆(要求用尺规作图,保留作图痕迹,不写作法);

(2)探究三角形的最小覆盖圆有何规律?请写出你所得到的结论(不要求证明);
(3)某地有四个村庄
 ,
, ,
, ,
, (其位置如图2所示),现拟建一个电视信号中转站,为了使这四个村庄的居民都能接收到电视信号,且使中转站所需发射功率最小(距离越小,所需功率越小),此中转站应建在何处?请说明理由.
(其位置如图2所示),现拟建一个电视信号中转站,为了使这四个村庄的居民都能接收到电视信号,且使中转站所需发射功率最小(距离越小,所需功率越小),此中转站应建在何处?请说明理由.
 搜索
搜索
 难度系数:0.85
难度系数:0.85  答案解析
答案解析
 有奖纠错
有奖纠错
