全一卷
1.下列运算正确的是( )
A. | B. | C. | D. |
2.一个自然数的算术平方根为 ,则和这个自然数相邻的下一个自然数是()
,则和这个自然数相邻的下一个自然数是()
 ,则和这个自然数相邻的下一个自然数是()
,则和这个自然数相邻的下一个自然数是()A. | B. | C. | D. |
3.太阳内部高温核聚变反应释放的辐射能功率为 千瓦,到达地球的仅占20亿分之一,到达地球的辐射能功率为()千瓦.(用科学计数法表示,保留2个有效数字)
千瓦,到达地球的仅占20亿分之一,到达地球的辐射能功率为()千瓦.(用科学计数法表示,保留2个有效数字)
 千瓦,到达地球的仅占20亿分之一,到达地球的辐射能功率为()千瓦.(用科学计数法表示,保留2个有效数字)
千瓦,到达地球的仅占20亿分之一,到达地球的辐射能功率为()千瓦.(用科学计数法表示,保留2个有效数字)A. | B. | C. | D. |
4.已知关于 的一元二次方程
的一元二次方程 的两个实数根是
的两个实数根是 ,且
,且
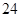 ,则
,则 的值是()
的值是()
 的一元二次方程
的一元二次方程 的两个实数根是
的两个实数根是 ,且
,且
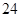 ,则
,则 的值是()
的值是()| A.8 | B. | C.6 | D.5 |
5.某班50名同学分别站在公路的A、B两点处,A、B两点相距1000米,A处有30人,B处有20人,要让两处的同学走到一起,并且使所有同学走的路程总和最小,那么集合地点应选在()


| A.A点处 |
B.线段 的中点处 的中点处 |
C.线段 上,距A点 上,距A点 米处 米处 |
D.线段 上,距A点400米处 上,距A点400米处 |
6.关于 的方程
的方程 有实数根,则整数
有实数根,则整数 的最大值是( )
的最大值是( )
 的方程
的方程 有实数根,则整数
有实数根,则整数 的最大值是( )
的最大值是( )| A.6 | B.7 | C.8 | D.9 |
7.甲、乙两盒中分别放入编号为1、2、3、4的形状相同的4个小球,从甲盒中任意摸出一球,再从乙盒中任意摸出一球,将两球编号数相加得到一个数,则得到数()的概率最大.
| A.3 | B.4 | C.5 | D.6 |
8.如图,小明要测量河内小岛B到河边公路l的距离,在A点测得 ,在C点测得
,在C点测得 ,又测得
,又测得 米,则小岛B到公路l的距离为【 】米.
米,则小岛B到公路l的距离为【 】米.

 ,在C点测得
,在C点测得 ,又测得
,又测得 米,则小岛B到公路l的距离为【 】米.
米,则小岛B到公路l的距离为【 】米.
| A.25 | B. | C. | D. |
9.已知圆O的半径为R,AB是圆O的直径,D是AB延长线上一点,DC是圆O的切线,C是切点,连结AC,若 ,则BD的长为( )
,则BD的长为( )

 ,则BD的长为( )
,则BD的长为( )
A. | B. | C. | D. |
10.如图,已知 中,
中, ,将
,将 绕顶点C顺时针旋转至
绕顶点C顺时针旋转至 的位置,且
的位置,且 三点在同一条直线上,则点A经过的最短路线的长度是()cm.
三点在同一条直线上,则点A经过的最短路线的长度是()cm.

 中,
中, ,将
,将 绕顶点C顺时针旋转至
绕顶点C顺时针旋转至 的位置,且
的位置,且 三点在同一条直线上,则点A经过的最短路线的长度是()cm.
三点在同一条直线上,则点A经过的最短路线的长度是()cm.
| A.8 | B. | C. | D. |
11.如图,在 中,
中, ,分别以
,分别以 为圆心,以
为圆心,以 的长为半径作圆,将
的长为半径作圆,将 截去两个扇形,则剩余(阴影)部分的面积为()cm2.
截去两个扇形,则剩余(阴影)部分的面积为()cm2.

 中,
中, ,分别以
,分别以 为圆心,以
为圆心,以 的长为半径作圆,将
的长为半径作圆,将 截去两个扇形,则剩余(阴影)部分的面积为()cm2.
截去两个扇形,则剩余(阴影)部分的面积为()cm2.
A. | B. | C. | D. |
12.在同一平面直角坐标系中,反比例函数 与一次函数
与一次函数 交于
交于 两点,O为坐标原点,则
两点,O为坐标原点,则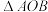 的面积为( )
的面积为( )
 与一次函数
与一次函数 交于
交于 两点,O为坐标原点,则
两点,O为坐标原点,则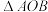 的面积为( )
的面积为( )| A.2 | B.6 | C.10 | D.8 |
13.分解因式:
______ .

14.方程 的解是
的解是________ .
 的解是
的解是15.在如图所示的方格纸中,每个小方格都是边长为1个单位的正方形, 的三个顶点都在格点上(每个小方格的顶点叫格点),画出
的三个顶点都在格点上(每个小方格的顶点叫格点),画出 绕点O逆时针旋转90°后的
绕点O逆时针旋转90°后的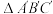 .
.

 的三个顶点都在格点上(每个小方格的顶点叫格点),画出
的三个顶点都在格点上(每个小方格的顶点叫格点),画出 绕点O逆时针旋转90°后的
绕点O逆时针旋转90°后的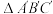 .
.
16.如图,正方形 的边长为10,点E在CB的延长线上,
的边长为10,点E在CB的延长线上, ,点P在边CD上运动(C、D两点除外),EP与AB相交于点F,若
,点P在边CD上运动(C、D两点除外),EP与AB相交于点F,若 ,四边形
,四边形 的面积为
的面积为 ,则
,则 关于
关于 的函数关系式是
的函数关系式是_________ .

 的边长为10,点E在CB的延长线上,
的边长为10,点E在CB的延长线上, ,点P在边CD上运动(C、D两点除外),EP与AB相交于点F,若
,点P在边CD上运动(C、D两点除外),EP与AB相交于点F,若 ,四边形
,四边形 的面积为
的面积为 ,则
,则 关于
关于 的函数关系式是
的函数关系式是
17.已知边长为 的正三角形
的正三角形 ,两顶点
,两顶点 分别在平面直角坐标系的
分别在平面直角坐标系的 轴、
轴、 轴的正半轴上滑动,点C在第一象限,连结OC,则OC的长的最大值是
轴的正半轴上滑动,点C在第一象限,连结OC,则OC的长的最大值是________ .

 的正三角形
的正三角形 ,两顶点
,两顶点 分别在平面直角坐标系的
分别在平面直角坐标系的 轴、
轴、 轴的正半轴上滑动,点C在第一象限,连结OC,则OC的长的最大值是
轴的正半轴上滑动,点C在第一象限,连结OC,则OC的长的最大值是
18.某蔬菜加工厂承担出口蔬菜加工任务,有一批蔬菜产品需要装入某一规格的纸箱.供应这种纸箱有两种方案可供选择:
方案一:从纸箱厂定制购买,每个纸箱价格为4元;
方案二:由蔬菜加工厂租赁机器自己加工制作这种纸箱,机器租赁费按生产纸箱数收取.工厂需要一次性投入机器安装等费用16000元,每加工一个纸箱还需成本费2.4元.
(1)若需要这种规格的纸箱 个,请分别写出从纸箱厂购买纸箱的费用
个,请分别写出从纸箱厂购买纸箱的费用 (元)和蔬菜加工厂自己加工制作纸箱的费用
(元)和蔬菜加工厂自己加工制作纸箱的费用 (元)关于
(元)关于 (个)的函数关系式;
(个)的函数关系式;
(2)假设你是决策者,你认为应该选择哪种方案?并说明理由.
方案一:从纸箱厂定制购买,每个纸箱价格为4元;
方案二:由蔬菜加工厂租赁机器自己加工制作这种纸箱,机器租赁费按生产纸箱数收取.工厂需要一次性投入机器安装等费用16000元,每加工一个纸箱还需成本费2.4元.
(1)若需要这种规格的纸箱
 个,请分别写出从纸箱厂购买纸箱的费用
个,请分别写出从纸箱厂购买纸箱的费用 (元)和蔬菜加工厂自己加工制作纸箱的费用
(元)和蔬菜加工厂自己加工制作纸箱的费用 (元)关于
(元)关于 (个)的函数关系式;
(个)的函数关系式;(2)假设你是决策者,你认为应该选择哪种方案?并说明理由.
19.新星公司到某大学从应届毕业生中招聘公司职员,对应聘者的专业知识、英语水平、参加社会实践与社团活动等三项进行测试或成果认定,三项的得分满分都为100分,三项的分数分别按5∶3∶2的比例记入每人的最后总分,有4位应聘者的得分如下表所示.

(1)写出4位应聘者的总分;
(2)就表中专业知识、英语水平、参加社会实践与社团活动等三项的得分,分别求出三项中4人所得分数的方差;
(3)由(1)和(2),你对应聘者有何建议?

(1)写出4位应聘者的总分;
(2)就表中专业知识、英语水平、参加社会实践与社团活动等三项的得分,分别求出三项中4人所得分数的方差;
(3)由(1)和(2),你对应聘者有何建议?
20.已知 ,延长BC到D,使
,延长BC到D,使 .取
.取 的中点
的中点 ,连结
,连结 交
交 于点
于点 .
.

(1)求 的值;
的值;
(2)若 ,求
,求 的长.
的长.
 ,延长BC到D,使
,延长BC到D,使 .取
.取 的中点
的中点 ,连结
,连结 交
交 于点
于点 .
.
(1)求
 的值;
的值;(2)若
 ,求
,求 的长.
的长.21.要对一块长60米、宽40米的矩形荒地 进行绿化和硬化.
进行绿化和硬化.
(1)设计方案如图①所示,矩形P、Q为两块绿地,其余为硬化路面,P、Q两块绿地周围的硬化路面宽都相等,并使两块绿地面积的和为矩形 面积的
面积的 ,求P、Q两块绿地周围的硬化路面的宽.
,求P、Q两块绿地周围的硬化路面的宽.
(2)某同学有如下设想:设计绿化区域为相外切的两等圆,圆心分别为 和
和 ,且
,且 到
到 的距离与
的距离与 到
到 的距离都相等,其余为硬化地面,如图②所示,这个设想是否成立?若成立,求出圆的半径;若不成立,说明理由.
的距离都相等,其余为硬化地面,如图②所示,这个设想是否成立?若成立,求出圆的半径;若不成立,说明理由.
 进行绿化和硬化.
进行绿化和硬化.(1)设计方案如图①所示,矩形P、Q为两块绿地,其余为硬化路面,P、Q两块绿地周围的硬化路面宽都相等,并使两块绿地面积的和为矩形
 面积的
面积的 ,求P、Q两块绿地周围的硬化路面的宽.
,求P、Q两块绿地周围的硬化路面的宽.(2)某同学有如下设想:设计绿化区域为相外切的两等圆,圆心分别为
 和
和 ,且
,且 到
到 的距离与
的距离与 到
到 的距离都相等,其余为硬化地面,如图②所示,这个设想是否成立?若成立,求出圆的半径;若不成立,说明理由.
的距离都相等,其余为硬化地面,如图②所示,这个设想是否成立?若成立,求出圆的半径;若不成立,说明理由.
22.如图所示,圆 是
是 的外接圆,
的外接圆,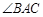 与
与 的平分线相交于点
的平分线相交于点 ,延长
,延长 交圆
交圆 于点
于点 ,连结
,连结 .
.

(1)求证: ;
;
(2)若圆 的半径为10cm,
的半径为10cm, ,求
,求 的面积.
的面积.
 是
是 的外接圆,
的外接圆,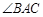 与
与 的平分线相交于点
的平分线相交于点 ,延长
,延长 交圆
交圆 于点
于点 ,连结
,连结 .
.
(1)求证:
 ;
;(2)若圆
 的半径为10cm,
的半径为10cm, ,求
,求 的面积.
的面积.23.在四边形 中,
中, ,且
,且 .取
.取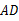 的中点
的中点 ,连结
,连结 .
.

(1)试判断三角形 的形状;
的形状;
(2)在线段 上,是否存在点
上,是否存在点 ,使
,使 .若存在,请求出
.若存在,请求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.
 中,
中, ,且
,且 .取
.取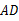 的中点
的中点 ,连结
,连结 .
.
(1)试判断三角形
 的形状;
的形状;(2)在线段
 上,是否存在点
上,是否存在点 ,使
,使 .若存在,请求出
.若存在,请求出 的长;若不存在,请说明理由.
的长;若不存在,请说明理由.24.如图,在平面直角坐标系 中,半径为1的圆的圆心
中,半径为1的圆的圆心 在坐标原点,且与两坐标轴分别交于
在坐标原点,且与两坐标轴分别交于 四点.抛物线
四点.抛物线 与
与 轴交于点
轴交于点 ,与直线
,与直线 交于点
交于点 ,且
,且 分别与圆
分别与圆 相切于点
相切于点 和点
和点 .
.
(1)求抛物线的解析式;
(2)抛物线的对称轴交 轴于点
轴于点 ,连结
,连结 ,并延长
,并延长 交圆
交圆 于
于 ,求
,求 的长.
的长.
(3)过点 作圆
作圆 的切线交
的切线交 的延长线于点
的延长线于点 ,判断点
,判断点 是否在抛物线上,说明理由.
是否在抛物线上,说明理由.
 中,半径为1的圆的圆心
中,半径为1的圆的圆心 在坐标原点,且与两坐标轴分别交于
在坐标原点,且与两坐标轴分别交于 四点.抛物线
四点.抛物线 与
与 轴交于点
轴交于点 ,与直线
,与直线 交于点
交于点 ,且
,且 分别与圆
分别与圆 相切于点
相切于点 和点
和点 .
.(1)求抛物线的解析式;
(2)抛物线的对称轴交
 轴于点
轴于点 ,连结
,连结 ,并延长
,并延长 交圆
交圆 于
于 ,求
,求 的长.
的长.(3)过点
 作圆
作圆 的切线交
的切线交 的延长线于点
的延长线于点 ,判断点
,判断点 是否在抛物线上,说明理由.
是否在抛物线上,说明理由.
 搜索
搜索
 难度系数:0.85
难度系数:0.85  答案解析
答案解析
 有奖纠错
有奖纠错
