搜索
全一卷
难度系数：0.85 
答案解析
有奖纠错
1．2的倒数是（ ）
| A．2 | B． | C． | D．-2 |
2．下列运算的结果中，是正数的是（）
| A．（﹣2014）﹣1 | B．﹣（2014）﹣1 |
| C．（﹣1）×（﹣2014） | D．（﹣2014）÷2014 |
3．如图1放置的一个机器零件，若其主（正）视图如图2，则其俯视图是（ ）
A． | B． | C． | D． |
4．一个袋子中装有6个红球3个白球，这些球除颜色外，形状、大小、质地等完全相同. 在看不到球的条件下，随机地从这个袋子中摸出一个球，摸到白球的概率为（ ）
A． | B． | C． | D． |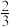
5．若关于x的一元二次方程的两个根为x1=1，x2=2，则这个方程可能是（ ）
| A．x2-3x+2=0 | B．x2+3x+2=0 | C．x2+3x-2=0 | D．x2-2x+3=0 |
6．如图，过A点的一次函数的图象与正比例函数y=2x的图象相交于点B，则这个一次函数的解析式是（ ）
| A．y=2x+3 | B．y=x﹣3 | C．y=2x﹣3 | D．y=﹣x+3 |
7．如图，将n个边长都为2的正方形按如图所示摆放，点A1，A2，…An分别是正方形的中心，则这n个正方形重叠部分的面积之和是（ ）
| A．n | B．n﹣1 | C．（ ）n﹣1 | D．（）n |
8．已知⊙O的半径r＝3，设圆心O到一条直线的距离为d，圆上到这条直线的距离为2的点的个数为m，给出下列命题：
①若d＞5，则m＝0；②若d＝5，则m＝1；③若1＜d＜5，则m＝3；④若d＝1，则m＝2；⑤若d＜1，则m＝4.
其中正确命题的个数是( )
①若d＞5，则m＝0；②若d＝5，则m＝1；③若1＜d＜5，则m＝3；④若d＝1，则m＝2；⑤若d＜1，则m＝4.
其中正确命题的个数是( )
| A．1 | B．2 | C．3 | D．5 |
9．分解因式：
－x=__________ ．
－x=10．分式方程
=1的解是___ ．
=1的解是11．如图，直线a、b被第三条直线c所截，如果a∥b，∠1=70°，那么∠3的度数是 ．
12．菱形的周长为20cm，两个相邻的内角的度数之比为1：2，则较长的对角线长度是________ cm．
13．在平面直角坐标系中，将点A（﹣1，2）向右平移3个单位长度得到点B，则点B关于x轴的对称点C的坐标是__ ．
14．如图，在Rt△ABC中，∠B＝90°，AB＝3，BC＝4，将△ABC折叠，使点B恰好落在边AC上，与点B′重合，AE为折痕，则
_______ ．
15．如图，已知AB为⊙O的直径，AB=2，AD和BE是圆O的两条切线，A、B为切点，过圆上一点C作⊙O的切线CF，分别交AD、BE于点M、N，连接AC、CB，若∠ABC=30°，则AM=____ ．
16．规定：sin（﹣x）=﹣sinx，cos（﹣x）=cosx，sin（x+y）=sinx•cosy+cosx•siny．
据此判断下列等式成立的是____ （写出所有正确的序号）
①cos（﹣60°）=﹣
；
②sin75°=
；
③sin2x=2sinx•cosx；
④sin（x﹣y）=sinx•cosy﹣cosx•siny．
据此判断下列等式成立的是
①cos（﹣60°）=﹣
；②sin75°=
；③sin2x=2sinx•cosx；
④sin（x﹣y）=sinx•cosy﹣cosx•siny．
17．（1）计算：
（2）化简：
．
（2）化简：
．18．如图，已知：在△AFD和△CEB中，点A、E、F、C在同一直线上，AE=CF，∠B=∠D，AD∥BC．求证：AD=BC．
19．我市中小学全面开展“阳光体育”活动，某校在大课间中开设了A：体操，B：跑操，C：舞蹈，D：健美操四项活动，为了解学生最喜欢哪一项活动，随机抽取了部分学生进行调查，并将调查结果绘制成了如下两幅不完整的统计图，请根据统计图回答下列问题：
(1)这次被调查的学生共有______人；
(2)请将统训图2补充完整；
(3)统计图1中B项目对应的扇形的圆心角是____度；
(4)已知该校共有学生3600人，请根据调查结果估计该校喜欢健美操的学生人数．
(1)这次被调查的学生共有______人；
(2)请将统训图2补充完整；
(3)统计图1中B项目对应的扇形的圆心角是____度；
(4)已知该校共有学生3600人，请根据调查结果估计该校喜欢健美操的学生人数．
20．在我市举行的中学生安全知识竞赛中共有20道题．每一题答对得5分，答错或不答都扣3分．
（1）小李考了60分，那么小李答对了多少道题？
（2）小王获得二等奖（75～85分），请你算算小王答对了几道题？
（1）小李考了60分，那么小李答对了多少道题？
（2）小王获得二等奖（75～85分），请你算算小王答对了几道题？
21．在平面直角坐标系中，若点P（x，y）的坐标x、y均为整数，则称点P为格点．若一个多边形的面积记为S，其内部的格点数记为N，边界上的格点数记为L．例如图中△ABC是格点三角形，对应的S＝1，N＝0，L＝4．
⑴ 写出图中格点四边形DEFG对应的S，N，L．
⑵ 已知任意格点多边形的面积公式为S＝N＋aL＋b，其中a，b为常数．当某格点多边形对应的N＝82，L＝38，求S的值．
⑴ 写出图中格点四边形DEFG对应的S，N，L．
⑵ 已知任意格点多边形的面积公式为S＝N＋aL＋b，其中a，b为常数．当某格点多边形对应的N＝82，L＝38，求S的值．
22．如图，一次函数y=﹣x+2的图象与反比例函数y=﹣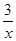
的图象交于A、B两点，与x轴交于D点，且C、D两点关于y轴对称．
（1）求A、B两点的坐标；
（2）求△ABC的面积．
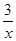的图象交于A、B两点，与x轴交于D点，且C、D两点关于y轴对称．（1）求A、B两点的坐标；
（2）求△ABC的面积．
23．如图，在△ABC中，以AC为直径作⊙O交BC于点D，交AB于点G，且D是BC中点，DE⊥AB，垂足为E，交AC的延长线于点F．
（1）求证：直线EF是⊙O的切线；
（2）若CF=5，cos∠A=
，求BE的长．
（1）求证：直线EF是⊙O的切线；
（2）若CF=5，cos∠A=
，求BE的长．
24．如图，已知抛物线y=x2+bx+c的顶点坐标为M（0，﹣1），与x轴交于A、B两点．
（1）求抛物线的解析式；
（2）判断△MAB的形状，并说明理由；
（3）过原点的任意直线（不与y轴重合）交抛物线于C、D两点，连接MC，MD，试判断MC、MD是否垂直，并说明理由．
（1）求抛物线的解析式；
（2）判断△MAB的形状，并说明理由；
（3）过原点的任意直线（不与y轴重合）交抛物线于C、D两点，连接MC，MD，试判断MC、MD是否垂直，并说明理由．
