全一卷
1. 的倒数是()
的倒数是()
 的倒数是()
的倒数是()A. | B. | C. | D. |
2.下列计算结果正确的是()
A. | B. |
C. | D. |
3.在下列四个图案中既是轴对称图形,又是中心对称图形的是( )
A. | B. | C. . . | D. |
4.2010年4月20日晚,“支援青海玉树抗震救灾义演晚会”在莱芜市政府广场成功举行,热心企业和现场观众踊跃捐款31083.58元.将31083.58元保留两位有效数字可记为( )
| A.3.1×106元 | B.3.11×104元 | C.3.1×104元 | D.3.10×105元 |
5.


A. | B. |
C. | D. |
6.如图所示的几何体是由一些小立方块搭成的,则这个几何体的俯视图是( )


A. | B. | C. | D. |
7.已知反比例函数 ,下列结论不正确的是()
,下列结论不正确的是()
 ,下列结论不正确的是()
,下列结论不正确的是()| A.图象必经过点(-1,2) | B.y随x的增大而增大 |
| C.图象在第二、四象限内 | D.若x>1,则y>-2 |
8.已知圆锥的底面半径长为5,侧面展开后得到一个半圆,则该圆锥的母线长为( )
| A.2.5 | B.5 | C.10 | D.15 |
9.二次函数 的图象如图所示,则一次函数
的图象如图所示,则一次函数 的图象不经过( )
的图象不经过( )

 的图象如图所示,则一次函数
的图象如图所示,则一次函数 的图象不经过( )
的图象不经过( )
| A.第一象限 | B.第二象限 |
| C.第三象限 | D.第四象限 |
10.已知 是二元一次方程组
是二元一次方程组 的解,则
的解,则 的算术平方根为
的算术平方根为
 是二元一次方程组
是二元一次方程组 的解,则
的解,则 的算术平方根为
的算术平方根为| A.4 | B.2 | C. | D.±2 |
11.一个边长为2的正多边形的内角和是其外角和的2倍,则这个正多边形的半径是( )
| A.2 | B. | C.1 | D. |
12.在一次自行车越野赛中,甲乙两名选手行驶的路程y(千米)随时间x(分)变化的图象(全程)如图,根据图象判定下列结论不正确的是( )


| A.甲先到达终点 |
| B.前30分钟,甲在乙的前面 |
| C.第48分钟时,两人第一次相遇 |
| D.这次比赛的全程是28千米 |
13.分解因式: .
.
 .
.14.有一组数据如下:2,3,a,5,6,它们的平均数是4,则这组数据的方差是_______.
15.某公司在2009年的盈利额为200万元,预计2011年的盈利额将达到242万元,若每年比上一年盈利额增长的百分率相同,那么该公司在2010年的盈利额为________万元.
16.在平面直角坐标系中,以点 、
、 、
、 为顶点的三角形向上平移3个单位,得到△
为顶点的三角形向上平移3个单位,得到△ (点
(点 分别为点
分别为点 的对应点),然后以点
的对应点),然后以点 为中心将△
为中心将△ 顺时针旋转
顺时针旋转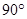 ,得到△
,得到△ (点
(点 分别是点
分别是点 的对应点),则点
的对应点),则点 的坐标是 .
的坐标是 .
 、
、 、
、 为顶点的三角形向上平移3个单位,得到△
为顶点的三角形向上平移3个单位,得到△ (点
(点 分别为点
分别为点 的对应点),然后以点
的对应点),然后以点 为中心将△
为中心将△ 顺时针旋转
顺时针旋转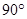 ,得到△
,得到△ (点
(点 分别是点
分别是点 的对应点),则点
的对应点),则点 的坐标是 .
的坐标是 .17.已知: ,
, ,
, ,…,观察上面的计算过程,寻找规律并计算
,…,观察上面的计算过程,寻找规律并计算 .
.
 ,
, ,
, ,…,观察上面的计算过程,寻找规律并计算
,…,观察上面的计算过程,寻找规律并计算 .
.18.(本题满分6分)先化简,再求值: ,其中
,其中 .
.
 ,其中
,其中 .
.19.2010年5月1日,第41届世博会在上海举办,世博知识在校园迅速传播.小明同学就本班学生对世博知识的了解程度进行了一次调查统计,下图是他采集数据后绘制的两幅不完整的统计图(A:不了解,B:一般了解,C:了解较多,D:熟悉).请你根据图中提供的信息解答以下问题:

(1)求该班共有多少名学生;
(2)在条形统计图中,将表示“一般了解”的部分补充完整;
(3)在扇形统计图中,计算出“了解较多”部分所对应的圆心角的度数;
(4)从该班中任选一人,其对世博知识的了解程度为“熟悉”的概率是多少?

(1)求该班共有多少名学生;
(2)在条形统计图中,将表示“一般了解”的部分补充完整;
(3)在扇形统计图中,计算出“了解较多”部分所对应的圆心角的度数;
(4)从该班中任选一人,其对世博知识的了解程度为“熟悉”的概率是多少?
20.(本题满分9分)
2009年首届中国国际航空体育节在莱芜雪野举办,期间在市政府广场进行了热气球飞行表演.如图,有一热气球到达离地面高度为36米的A处时,仪器显示正前方一高楼顶部B的仰角是37°,底部C的俯角是60°.为了安全飞越高楼,气球应至少再上升多少米?

(结果精确到0.1米)
(参考数据:
 )
)
2009年首届中国国际航空体育节在莱芜雪野举办,期间在市政府广场进行了热气球飞行表演.如图,有一热气球到达离地面高度为36米的A处时,仪器显示正前方一高楼顶部B的仰角是37°,底部C的俯角是60°.为了安全飞越高楼,气球应至少再上升多少米?

(结果精确到0.1米)
(参考数据:

 )
)21.(本题满分9分)在Rt△ACB中,∠C=90°,AC=3cm,BC=4cm,以BC为直径作⊙O交AB于点D.

(1)求线段AD的长度;
(2)点E是线段AC上的一点,试问当点E在什么位置时,直线ED与⊙O相切?请说明理由.

(1)求线段AD的长度;
(2)点E是线段AC上的一点,试问当点E在什么位置时,直线ED与⊙O相切?请说明理由.
22.某中学为落实市教育局提出的“全员育人,创办特色学校”的会议精神,决心打造“书香校园”,计划用不超过1900本科技类书籍和1620本人文类书籍,组建中、小型两类图书角共30个.已知组建一个中型图书角需科技类书籍80本,人文类书籍50本;组建一个小型图书角需科技类书籍30本,人文类书籍60本.
(1)符合题意的组建方案有几种?请你帮学校设计出来;
(2)若组建一个中型图书角的费用是860元,组建一个小型图书角的费用是570元,试说明(1)中哪种方案费用最低,最低费用是多少元?
(1)符合题意的组建方案有几种?请你帮学校设计出来;
(2)若组建一个中型图书角的费用是860元,组建一个小型图书角的费用是570元,试说明(1)中哪种方案费用最低,最低费用是多少元?
23.在 ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连结EG、GF、FH、HE.
ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连结EG、GF、FH、HE.
(1)如图①,试判断四边形EGFH的形状,并说明理由;
(2)如图②,当EF⊥GH时,四边形EGFH的形状是 ;
(3)如图③,在(2)的条件下,若AC=BD,四边形EGFH的形状是 ;
(4)如图④,在(3)的条件下,若AC⊥BD,试判断四边形EGFH的形状,并说明理由.

 ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连结EG、GF、FH、HE.
ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连结EG、GF、FH、HE.(1)如图①,试判断四边形EGFH的形状,并说明理由;
(2)如图②,当EF⊥GH时,四边形EGFH的形状是 ;
(3)如图③,在(2)的条件下,若AC=BD,四边形EGFH的形状是 ;
(4)如图④,在(3)的条件下,若AC⊥BD,试判断四边形EGFH的形状,并说明理由.

24.(本题满分12分)如图,在平面直角坐标系中,已知抛物线 交
交 轴于
轴于 两点,交
两点,交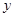 轴于点
轴于点 .
.

(1)求此抛物线的解析式;
(2)若此抛物线的对称轴与直线 交于点D,作⊙D与x轴相切,⊙D交
交于点D,作⊙D与x轴相切,⊙D交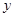 轴于点E、F两点,求劣弧
轴于点E、F两点,求劣弧 的长;
的长;
(3)P为此抛物线在第二象限图像上的一点,PG垂直于 轴,垂足为点G,试确定P点的位置,使得△PGA的面积被直线AC分为1︰2两部分.
轴,垂足为点G,试确定P点的位置,使得△PGA的面积被直线AC分为1︰2两部分.
 交
交 轴于
轴于 两点,交
两点,交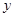 轴于点
轴于点 .
.
(1)求此抛物线的解析式;
(2)若此抛物线的对称轴与直线
 交于点D,作⊙D与x轴相切,⊙D交
交于点D,作⊙D与x轴相切,⊙D交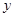 轴于点E、F两点,求劣弧
轴于点E、F两点,求劣弧 的长;
的长;(3)P为此抛物线在第二象限图像上的一点,PG垂直于
 轴,垂足为点G,试确定P点的位置,使得△PGA的面积被直线AC分为1︰2两部分.
轴,垂足为点G,试确定P点的位置,使得△PGA的面积被直线AC分为1︰2两部分. 搜索
搜索
 难度系数:0.94
难度系数:0.94  答案解析
答案解析
 有奖纠错
有奖纠错
