搜索
全一卷
难度系数：0.85 
答案解析
有奖纠错
1．若（ ）﹣（﹣2）=3，则括号内的数是（ ）
| A．﹣1 | B．1 | C．5 | D．﹣5 |
2．下列计算正确的是（ ）
A． |
B． |
C． |
D． |
3．下列四个几何体：
其中左视图与俯视图相同的几何体共有（ ）
其中左视图与俯视图相同的几何体共有（ ）
| A．1个 | B．2个 | C．3个 | D．4个 |
4．地球的表面积约为510000000km2，将510000000用科学记数法表示为（ ）
| A．0.51×109 | B．5.1×108 | C．5.1×109 | D．51×107 |
5．如图，AB//CD，∠1=58°，FG平分∠EFD，则∠FGB的度数等于（ ）
| A．122° | B．151° | C．116° | D．97° |
6．如图，在方格纸中，随机选择标有序号①②③④⑤中的一个小正方形涂黑，与图中阴影部分构成轴对称图形的概率是( )
A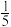． | B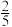． | C． | D． |
7．小亮的妈妈用28元钱买了甲、乙两种水果，甲种水果每千克4元，乙种水果每千克6元，且乙种水果比甲种水果少买了2千克，求小亮妈妈两种水果各买了多少千克？设小亮妈妈买了甲种水果x千克，乙种水果y千克，则可列方程组为（）
A． | B． |
C． | D． |
8．化简：（a+
）（1﹣
）的结果等于（ ）
）（1﹣
）的结果等于（ ）| A．a﹣2 | B．a+2 | C． | D． |
9．如图，⊙O是△ABC的外接圆，∠B=60°，⊙O的半径为4，则AC的长等于（ ）
A．4 | B．6 | C．2 | D．8 |
10．若十位上的数字比个位上的数字、百位上的数字都大的三位数叫做中高数，如796就是一个“中高数”．若十位上数字为7，则从3、4、5、6、8、9中任选两数，与7组成“中高数”的概率是（ ）
A． | B． | C． | D． |
11．某单位若干名职工参加普法知识竞赛，将成绩制成如图所示的扇形统计图和条形统计图，根据图中提供的信息，这些职工成绩的中位数和平均数分别是（ ）
| A．94分，96分 | B．96分，96分 |
| C．94分，96.4分 | D．96分，96.4分 |
12．不等式组
的整数解有( )
的整数解有( )| A．1个 | B．2个 | C．3个 | D．4个 |
13．如图，AD是△ABC的角平分线，DE⊥AC，垂足为E，
交ED的延长线于点F，若BC恰好平分∠ABF，AE=2BF，给出下列四个结论：①DE=DF；②DB=DC；③AD⊥BC；④AC=3BF，其中正确的结论共有（ ）
交ED的延长线于点F，若BC恰好平分∠ABF，AE=2BF，给出下列四个结论：①DE=DF；②DB=DC；③AD⊥BC；④AC=3BF，其中正确的结论共有（ ） | A．4个 | B．3个 | C．2个 | D．1个 |
14．如图，轮船从B处以每小时60海里的速度沿南偏东20°方向匀速航行，在B处观测灯塔A位于南偏东50°方向上，轮船航行40分钟到达C处，在C处观测灯塔A位于北偏东10°方向上，则C处与灯塔A的距离是( )
| A．20海里 | B．40海里 | C． 海里 | D． 海里 |
15．如图，在平面直角坐标系中，正三角形OAB的顶点B的坐标为（2，0），点A在第一象限内，将△OAB沿直线OA的方向平移至△O′A′B′的位置，此时点A′的横坐标为3，则点B′的坐标为（ ）
| A．（4，2） | B．（3，3） | C．（4，3） | D．（3，2） |
16．在同一坐标系中，一次函数
与二次函数
的图象可能是（ ）．
与二次函数的图象可能是（ ）．A． | B． | C． | D． |
17．如图，菱形ABCD的边长为2，∠A=60°，以点B为圆心的圆与AD、DC相切，与AB、CB的延长线分别相交于点E、F，则图中阴影部分的面积为（）
A． | B． | C． | D． |
18．下面每个表格中的四个数都是按相同规律填写的：
根据此规律确定x的值为（ ）
根据此规律确定x的值为（ ）
| A．135 | B．170 | C．209 | D．252 |
19．某同学在用描点法画二次函数
的图象时，列出了下面的表格：
由于粗心，他算错了其中一个y值，则这个错误的数值是（）
的图象时，列出了下面的表格：
由于粗心，他算错了其中一个y值，则这个错误的数值是（）
| A．﹣11 | B．﹣2 | C．1 | D．﹣5 |
20．如图，在长方形ABCD中，E是AD的中点，将△ABE沿直线BE折叠后得到△GBE，延长BG交CD于点F，连结EF，若AB＝6，BC＝4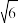
，则FD的长为( )
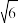，则FD的长为( )
| A．2 | B．4 | C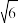． | D．2 |
21．分解因式： 
= ______________
= 22．方程：（2x+1）（x﹣1）=8（9﹣x）﹣1的根的情况是_______ .
23．(2015·泰安)如图，在矩形ABCD中，M，N分别是边AD，BC的中点，E，F分别是线段BM，CM的中点．若AB＝8，AD＝12，则四边形ENFM的周长为_____ ．
24．如图，AB是⊙O的直径，且经过弦CD的中点H，过CD延长线上一点E作⊙O的切线，切点为F．若∠ACF=65°，则∠E=_________ ．
25．某服装店购进一批甲、乙两种款型时尚T恤衫，甲种款型共用了7800元，乙种款型共用了6400元，甲种款型的件数是乙种款型件数的1.5倍，甲种款型每件的进价比乙种款型每件的进价少30元．
（1）甲、乙两种款型的T恤衫各购进多少件？
（2）商店进价提高60%标价销售，销售一段时间后，甲款型全部售完，乙款型剩余一半，商店决定对乙款型按标价的五折降价销售，很快全部售完，求售完这批T恤衫商店共获利多少元？
（1）甲、乙两种款型的T恤衫各购进多少件？
（2）商店进价提高60%标价销售，销售一段时间后，甲款型全部售完，乙款型剩余一半，商店决定对乙款型按标价的五折降价销售，很快全部售完，求售完这批T恤衫商店共获利多少元？
26．一次函数
与反比例函数
的图象相交于A（﹣1，4），B（2，n）两点，直线AB交x轴于点
与反比例函数
的图象相交于A（﹣1，4），B（2，n）两点，直线AB交x轴于点A． （1）求一次函数与反比例函数的表达式； （2）过点B作BC⊥y轴，垂足为C，连接AC交x轴于点E，求△AED的面积S． |
27．如图，在△ABC中，AB=AC，点P、D分别是BC、AC边上的点，且∠APD=∠B,
（1）求证：AC•CD=CP•BP；
（2）若AB=10，BC=12，当PD∥AB时，求BP的长．
（1）求证：AC•CD=CP•BP；
（2）若AB=10，BC=12，当PD∥AB时，求BP的长．
28．如图，△ABC是直角三角形，且∠ABC=90°，四边形BCDE是平行四边形，E为AC中点，BD平分∠ABC，点F在AB上，且BF=BC．
求证：（1）DF=AE；
（2）DF⊥AC．
求证：（1）DF=AE；
（2）DF⊥AC．
29．如图，抛物线y=ax2+bx+c为x轴的一交点为A（﹣6，0），与y轴的交点为C（0，3），且经过点G（﹣2，3）．
(1)求抛物线的表达式.
(2)点P是线段OA上一动点，过P作平行于y轴的直线与AC交于点Q，设△CPQ的面积为S，求S的最大值.
(3)若点B是抛物线与x轴的另一定点，点D、M在线段AB上，点N在线段AC上，∠DCB=∠CDB，CD是MN的垂直平分线，求点M的坐标．
(1)求抛物线的表达式.
(2)点P是线段OA上一动点，过P作平行于y轴的直线与AC交于点Q，设△CPQ的面积为S，求S的最大值.
(3)若点B是抛物线与x轴的另一定点，点D、M在线段AB上，点N在线段AC上，∠DCB=∠CDB，CD是MN的垂直平分线，求点M的坐标．
